
- •ЛинейнОе пространство
- •Определения. Базис и размерность. Разложение вектора по базису пространства
- •Определение базиса и размерность пространства l
- •Если обладает базисом, то говорят, что линейное пространствоLимеет рангQ (ranq q).
- •Изоморфизм n-мерных линейных пространств
- •Формулы преобразования координат при изменении базиса
- •Произведением. Евклидово пространство
- •2.1. Определение евклидова пространства. Длина вектора. Неравенство Коши-Буняковского
- •2.2. Ортогональный и орто-нормированный базисы в пространстве е
- •2.3. Ортогонализация базиса в пространстве
- •2.4. Скалярное произведение векторов в евклидовом пространстве
- •Изоморфизм евклидовых пространств
- •§ 3. Билинейные квадратичные формы
- •4.1. Линейная функция
- •4.2. Билинейные формы
- •4.3. Матрицы билинейной формы
- •4.4. Преобразование матрицы билинейной формы при изменении базиса
- •4.5. Квадратичные формы
- •4.6. Методы приведения квадратичной формы к каноническому виду
- •Будем рассматривать квадратичную форму (7) в евклидовом пространстве
Г л а в а Ш. ПРОСТРАНСТВА
ЛинейнОе пространство
Определения. Базис и размерность. Разложение вектора по базису пространства
ОПРЕДЕЛЕНИЕ 1. Множество L называется линейным, если для элементов этого множества выполнены следующие условия:
а) в L
введено сложение элементов, то есть
![]() введено отображение
введено отображение
![]() ,
(1)
,
(1)
обладающее следующими свойствами:
![]()
![]() ,
,
![]()
![]()
![]() такой, что
такой, что
![]() ,
,
![]() ,
,
(элемент -![]() называется противоположным элементу
называется противоположным элементу![]() );
);
б) в множестве
L
введена операция умножения элементов
на действительные числа, то есть
![]() и
и![]() определено отображение
определено отображение
![]() ,
,
обладающее свойствами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следует отметить, что элементами линейного пространства , как правило, являются векторы.
ОПРЕДЕЛЕНИЕ 2. Пространство L называется действительным, если в L операция умножения векторов на число определена только для действительных чисел, и - комплексным, если эта операция определена для комплексных чисел.
ОПРЕДЕЛЕНИЕ 3.
Система векторов
![]() называетсялинейно
зависимой,
если найдутся такие числа
называетсялинейно
зависимой,
если найдутся такие числа
![]() ,
что
,
что
![]() ,
(2)
,
(2)
причем
![]() ,
(3)
,
(3)
и эта система векторов называется линейно независимой, если
 (4)
(4)
Условие
![]() означает, что среди всех
означает, что среди всех![]() существует
хотя бы одно число не равное нулю.
существует
хотя бы одно число не равное нулю.
Т е о р е м а 1. Если
система векторов
![]() является линейно зависимой, то один
из векторов этой системы является
линейной комбинацией остальных.
является линейно зависимой, то один
из векторов этой системы является
линейной комбинацией остальных.
Д о к а з а т е л ь
с т в о. Запишем условие линейной
зависимости векторов
![]()
 .
(5)
.
(5)
Пусть для
определенности
![]() ,
тогда из (5) имеем:
,
тогда из (5) имеем:
![]() .
.
Таким образом,
вектор
![]() является линейной комбинацией остальных
векторов.
является линейной комбинацией остальных
векторов.
Определение базиса и размерность пространства l
Пусть
![]() - произвольное множество векторов
линейного пространства.
- произвольное множество векторов
линейного пространства.
ОПРЕДЕЛЕНИЕ 4.
Упорядоченная система векторов
![]()
называется базисом в Q, если:
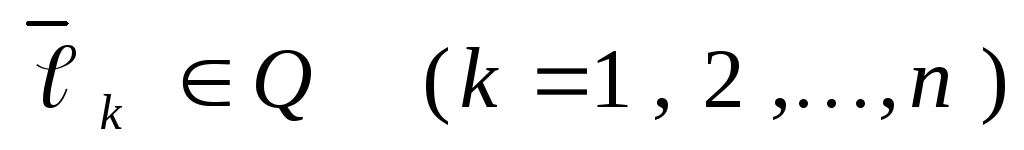 ;
;
б) система векторов
![]() линейно независимая;
линейно независимая;
в) для
![]() найдутся такие числа
найдутся такие числа![]() ,
что
,
что
![]() .
(6)
.
(6)
Формула (6) называется
разложением
вектора
![]() по базису Q
, а коэффициенты
по базису Q
, а коэффициенты
![]() –
координатами этого вектора в базисеQ.
–
координатами этого вектора в базисеQ.
Если обладает базисом, то говорят, что линейное пространствоLимеет рангQ (ranq q).
ОПРЕДЕЛЕНИЕ 5.
Линейное пространство L
называется n-мерным,
если в нем существует n
линейно независимых векторов и
обозначается так
![]() .
В противном случае, пространствоL
называется бесконечно
мерным.
.
В противном случае, пространствоL
называется бесконечно
мерным.
Т е о р е м а 2.
Каждый вектор
![]() из
из![]() можно представить, и притом единственным
образом, как линейную комбинацию векторов
базиса.
можно представить, и притом единственным
образом, как линейную комбинацию векторов
базиса.
Д о к а з а т е л ь
с т в о. Пусть векторы
![]() образуют базис в
образуют базис в![]() .
Присоединим к ним произвольный вектор
.
Присоединим к ним произвольный вектор![]() .
Система векторов состоит уже из
.
Система векторов состоит уже из![]() -го
вектора
-го
вектора![]() .
Поэтому по определениюn-мерного
пространства они должны быть линейно
зависимыми, то есть
.
Поэтому по определениюn-мерного
пространства они должны быть линейно
зависимыми, то есть
![]() ,
(7)
,
(7)
причем
![]() .
.
Число
![]() заведомо отлично от нуля, так как иначе
из формулы (7) следовала бы линейная
зависимость векторов
заведомо отлично от нуля, так как иначе
из формулы (7) следовала бы линейная
зависимость векторов![]() .
Выразим из (7) вектор
.
Выразим из (7) вектор![]() .
.
![]() .
(7)
.
(7)
Таким образом,
мы доказали, что каждый вектор
![]() есть линейная комбинация векторов
базиса
есть линейная комбинация векторов
базиса![]() .
Докажем, что вектор
.
Докажем, что вектор![]() разлагается единственным образом по
базису
разлагается единственным образом по
базису![]() .
.
Доказательство проведем от противного.
Пусть существует два разложения
![]() (8)
(8)
и
![]() .
(9)
.
(9)
Вычитая из (8) разложение (9), получим:
![]() .
(10)
.
(10)
Так как вектора
базиса
![]() .линейно
независимые, то (10) возможно лишь, если:
.линейно
независимые, то (10) возможно лишь, если:
![]() .
.
Что и требовалось доказать.
