
- •Глава 1. Матрицы и их определители
- •§1. Матрицы
- •Линейные операции над матрицами
- •2 · .
- •§2.Определитель матрицы. Свойства определителя правила его вычисления
- •Теперь рассмотрим матрицу третьего порядка
- •Определителем этой матрицы называется число, равное
- •Свойства определителя
- •§3. Обратная матрица
- •§4. Разложение матрицы на произведение двух треугольных матриц
- •§5. Клеточные матрицы и действия над ними
- •§6. Определение ранга матрицы и основные методы его вычисления
- •Теорема о ранге матрицы . Базисный минор
Теорема о ранге матрицы . Базисный минор
Рассмотрим n матриц-столбцов (строк)

и их сумму
![]() ,
,
которая называется
линейной
комбинацией матриц-столбцов,
а числа
![]() -коэффициентами
этой комбинации.
-коэффициентами
этой комбинации.
ОПРЕДЕЛЕНИЕ 1.
Матрицы-столбцы![]() называютсялинейно-зависимыми,
если существуют действительные числа
называютсялинейно-зависимыми,
если существуют действительные числа
![]() такие, что
такие, что
![]() =0 ,
(1)
=0 ,
(1)
причем
![]()
![]()
ПРИМЕР 1. Матрицы столбцы
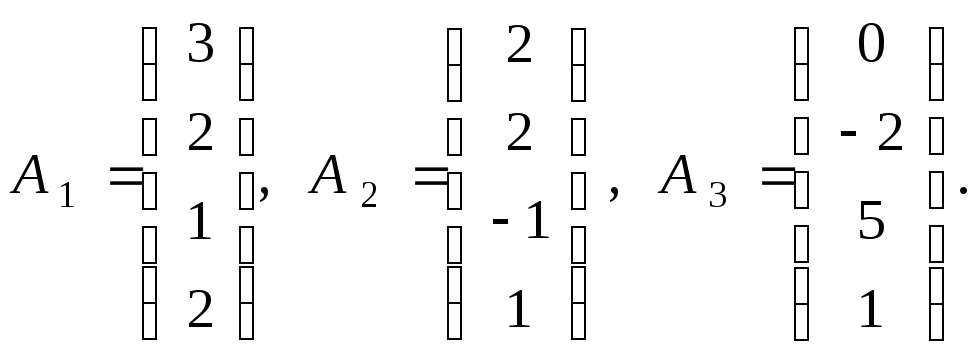
линейно зависимы, так как
![]()
 .
.
ОПРЕДЕЛЕНИЕ 2.
Матрицы-столбцы![]() называютсялинейно-независимыми,
если существуют действительные числа
называютсялинейно-независимыми,
если существуют действительные числа
![]() такие, что
такие, что
![]() 0 ,
(6)
0 ,
(6)
причем
![]()
![]()
ПРИМЕР 2. Матрицы столбцы

 .
.
Т е о р е м а. Если ранг матрицы A равен r, то :
а) она имеет r независимых столбцов и r независимых строк, которые называются базисными;
б) любой столбец (строка) этой матрицы выражается в виде линейной комбинации базисных столбцов (строк).
Д о к а з а т е л ь с т в о. Пусть дана матрица

ранг которой равен r . Следовательно у матрицы A существует хотя бы один минор порядка r отличный от нуля, который будем называть базисным, а столбцы и строки, из которых он составлен - базисными столбцами и строками матрицы. Введем обозначение для столбцов матрицы A:
 .
.
Предположим для
определенности, что базисный минор
матрицы A
расположен в левом верхнем углу и
обозначим его через
![]()
 .
.
Тогда базисными
столбцами будут
![]() .
Далее предположим, что эти столбцы
линейно зависимы, то есть существуют
числа
.
Далее предположим, что эти столбцы
линейно зависимы, то есть существуют
числа![]() не все равные нулю,
такие что:
не все равные нулю,
такие что:
![]() =0 ,
=0 ,
или

![]()
Пусть![]() .
Умножим первый столбец минора
.
Умножим первый столбец минора![]() на
на
![]() и прибавим
к нему остальные столбцы, умноженные
соответственно на 2
,3
,...,n:
и прибавим
к нему остальные столбцы, умноженные
соответственно на 2
,3
,...,n:

Последнее равенство
невозможно, так как
![]()
![]() Значит
предположение о линейной зависимости
базисных столбцов неверно. Следовательно,
они линейно независимы.
Значит
предположение о линейной зависимости
базисных столбцов неверно. Следовательно,
они линейно независимы.
Построим теперь
определитель (r+1)-го
порядка приписав справа к базисному
минору
![]() любой столбец матрицыA,
а снизу любую строку этой матрицы:
любой столбец матрицыA,
а снизу любую строку этой матрицы:

Если
![]() или
или![]() i,
то
i,
то ![]() имеет два одинаковых
столбца или две одинаковые строки,
поэтому
имеет два одинаковых
столбца или две одинаковые строки,
поэтому
![]() .
Еслиk
r и i
r, то
.
Еслиk
r и i
r, то
![]() - минор порядка(r+1)
матрицы A и
он равен нулю (ранг матрицы A
равен r).
Следовательно, во всех случаях
- минор порядка(r+1)
матрицы A и
он равен нулю (ранг матрицы A
равен r).
Следовательно, во всех случаях
![]() .
Разложим этот определитель по элементам
последней строки:
.
Разложим этот определитель по элементам
последней строки:
![]() .
.
Алгебраические
дополнения
![]() не зависят от того, какая i-я строка
приписана в
не зависят от того, какая i-я строка
приписана в![]() снизу, так как алгебраические дополнения
получаются вычеркиванием этой строки.
Обозначим эти алгебраические дополнения
соответственно символами
снизу, так как алгебраические дополнения
получаются вычеркиванием этой строки.
Обозначим эти алгебраические дополнения
соответственно символами![]() 1,
2,
..., r,
k.
Беря в качестве i-й
строки первую, затем вторую и т.д. строки
матрицы A,
получим из
последнего равенства:
1,
2,
..., r,
k.
Беря в качестве i-й
строки первую, затем вторую и т.д. строки
матрицы A,
получим из
последнего равенства:

или
![]()
где
![]() столбцы матрицыA.
Так как
столбцы матрицыA.
Так как![]()
![]() ,
то, введя обозначения
,
то, введя обозначения![]()
 получим окончательно
получим окончательно![]() то есть любой столбец матрицыA
есть линейная
комбинация базисных столбцов, что и
требовалось доказать.
то есть любой столбец матрицыA
есть линейная
комбинация базисных столбцов, что и
требовалось доказать.
ПРИМЕР. Выяснить,
является ли система векторов
![]()
![]() и
и![]() линейно зависимой или линейно независимой.
линейно зависимой или линейно независимой.
Запишем матрицу
A,
столбцами которой являются векторы
![]() и
и![]()
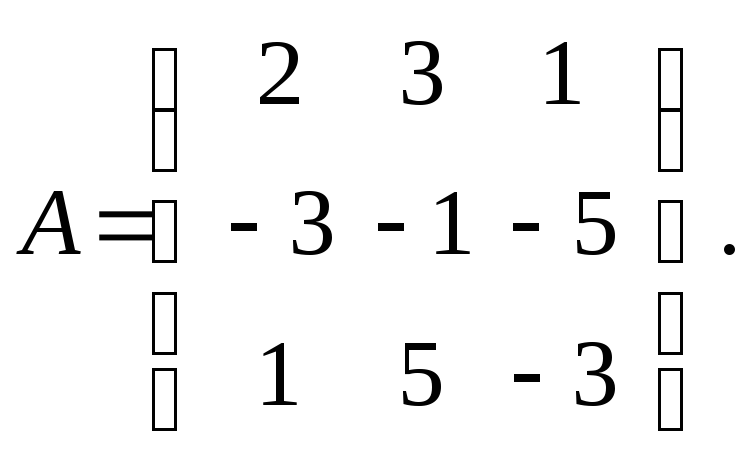
Далее вычислим
ранг этой матрицы. Имеем
![]() ,
,![]() Следовательно,rankA=2.
По теореме о базисном миноре исходная
система векторов
Следовательно,rankA=2.
По теореме о базисном миноре исходная
система векторов
![]() и
и![]() линейно зависима. Так как минор второго
порядка отличен от нуля, то он может
быть принят за базисный минором, а
векторы
линейно зависима. Так как минор второго
порядка отличен от нуля, то он может
быть принят за базисный минором, а
векторы![]() и
и![]() образуют базис исходной системы векторов.
образуют базис исходной системы векторов.
