§2.Определитель матрицы. Свойства определителя правила его вычисления

Пусть А - произвольная квадратная матрица порядка n

A=.

С матрицей А связно понятие определителя (детерминанта), который принято обозначать так A  или det A:

A =det A = . (1)

Определитель матрицы есть число, вычисляемое по некоторым правилам, которые мы рассмотрим ниже.

Во-первых, следует отметить, что в определителе различают две диагонали: главную и побочную. Главная диагональ (так же, как и в квадратной матрице) состоит из элементов a_ii, где i=1, 2, 3, ... , n. Побочная диагональ проходит перпендикулярно главной из верхнего правого угла определителя в нижний левый. Порядок определителя соответствует порядку матрицы, определителем которой он является.

Если порядок матрицы равен единице, то есть эта матрица состоит из одного элемента a_ij, то определителем первого порядка , соответствующем такой матрице, называется число, равное этому элементу.

Пусть дана квадратная матрица второго порядка:

.

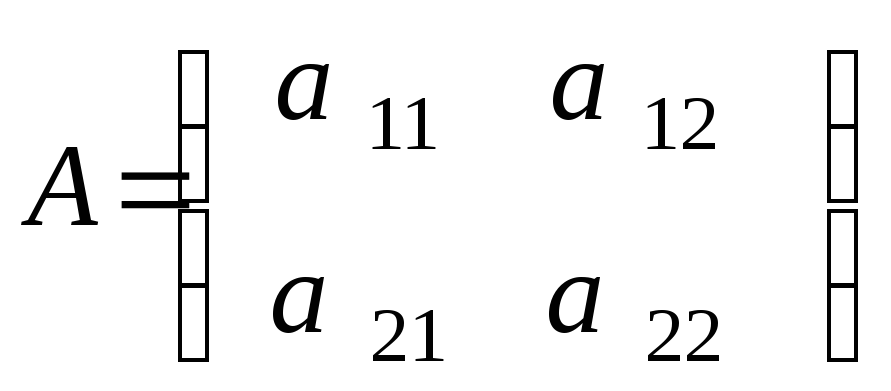Определителем второго порядка, соответствующим этой матрице называется число

. (2)

Из формулы (2) следует, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали минус произведение элементов, стоящих на побочной диагонали.

ПРИМЕР 1. Вычислить определитель матрицы A=.

det A=.

Теперь рассмотрим матрицу третьего порядка

Определителем этой матрицы называется число, равное

(3)

Из выражения (3) следует, что каждый член определителя прежде всего представляет собой произведение трех его элементов, взятых по одному из каждой строки и каждого столбца: со знаком плюс - три члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах равнобедренных треугольников с основаниями, параллельными главной диагонали; со знаком минус - три члена, расположенных аналогичным образом относительно побочной диагонали. Схема вычисления определителя третьего порядка изображена на следующих рисунках:

.

ПРИМЕР. Вычислить определитель матрицы

det A==1·5·2 +3·1·(-4)+2·(-1) ·2 - 2·5·3 - 1·(-1) ·1 - 2· (-4) ·2= -13.

Указанное правило вычисления определителя третьего порядка называется правилом треугольников.

Наряду с правилом треугольников для вычисления определителей третьего порядка существует правило Саросса . Суть этого правила состоит в том, что справа к исходному определителю добавляются первый и второй столбцы этого определителя, то есть:

.

Алгоритм вычисления определителя третьего порядка по правилу Сарроса заключается в том, что в исходной сумме (3) со знаком плюс берутся члены, состоящие из произведения элементов, находящихся на главной диагонали и двух прямых, которые параллельны этой диагонали и расположены выше ее, а со знаком минус берутся элементы, лежащие на побочной диагонали и двух прямых, параллельных этой прямой и расположенных ниже нее.

Рассмотрим теперь вопрос о вычислении определителя порядка n, где n4. Для вычисления такого определителя необходимо ввести понятия минора и алгебраического дополнения.

ОПРЕДЕЛЕНИЕ 8. Минором элемента a_ij делителя n-го порядка (1) называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-й строки и j-го столбца, то есть той строки и того столбца, на пересечении которых стоит элемент a_ij.

Минор элемента a_ij обозначается M_ij. Здесь первый индекс означает номер строки, второй - номер столбца, которые вычеркиваются из исходного определителя. Например, в определителе третьего порядка

минором элемента является определитель второго порядка

,

а для элемента a₃₂ минор – определитель:

.

ОПРЕДЕЛЕНИЕ 9. Алгебраическим дополнением элемента а_ij определителя n-го порядка (1) называется число

Ниже приведем без доказательства известную теорему Лапласа о вычислении определителя n-го порядка.

Т е о р е м а 1 (Л а п л а с с а). Определитель равен сумме произведений элементов любой его строки (столбца), на соответствующее ему алгебраическое дополнение:

detA = =

(4)

или

detA= (5)

Формула (4) называется формулой разложения определителя по элементам i-й строки, а формула (5) - разложением определителя по элементам j-го столбца.

ПРИМЕР 3. Вычислить определитель , разложив его по элементам 1-й строки.

Согласно формуле (4) имеем

.

Так как

то

.

ПРИМЕР 4. Вычислить определитель , разложив его по элементам 2-го столбца.

По формуле (5) получаем

.

Далее, находим

Откуда

.

Т е о р е м а 2 (следствие из теоремы 1). Если все элементы i-й строки (столбца) определителя A, кроме одного, например, a_ik, равны нулю, то определитель равен произведению элемента a_ik на его алгебраическое дополнение:

ПРИМЕР 4. Вычислить определитель четвертого порядка

разложив его по элементам 2-го столбца.

Так как то по формуле (5) получаем

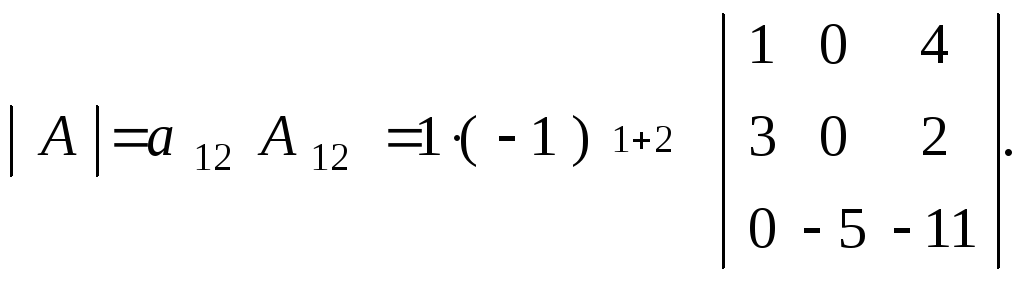
Откуда, снова разлагая полученный определитель третьего порядка по элементам 2-го столбца, находим

Т е о р е м а 3. Сумма произведений элементов какой-либо строки или столбца определителя на алгебраические дополнения соответствующих элементов параллельной строки (или столбца) равна нулю.

Так, для определителя третьего порядка

на основании теоремы 3, справедливы равенства: