
- •Глава 1. Матрицы и их определители
- •§1. Матрицы
- •Линейные операции над матрицами
- •2 · .
- •§2.Определитель матрицы. Свойства определителя правила его вычисления
- •Теперь рассмотрим матрицу третьего порядка
- •Определителем этой матрицы называется число, равное
- •Свойства определителя
- •§3. Обратная матрица
- •§4. Разложение матрицы на произведение двух треугольных матриц
- •§5. Клеточные матрицы и действия над ними
- •§6. Определение ранга матрицы и основные методы его вычисления
- •Теорема о ранге матрицы . Базисный минор
Глава 1. Матрицы и их определители
§1. Матрицы
оПРЕДЕЛЕНИЕ 1. Матрицей называется совокупность вещественных или
комплексных чисел
![]() ,расположенных
в виде прямоугольной таблицы
,расположенных
в виде прямоугольной таблицы
A=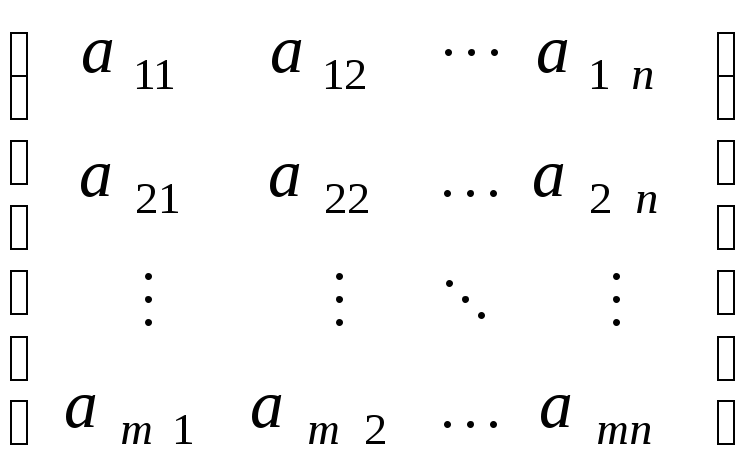 .
.
Числа
![]()
![]() называются элементами
матрицы.
Индексы i,,j
означают,
что элемент
называются элементами
матрицы.
Индексы i,,j
означают,
что элемент
![]() расположен на пересеченииi-й
строки и j-го
столбца матрицы A=
расположен на пересеченииi-й
строки и j-го
столбца матрицы A=![]() (i=1,2,...,m;
j=1,2,...,n).
(i=1,2,...,m;
j=1,2,...,n).
Если в матрице A mn, то матрица называется прямоугольной. В случае, когда m=n, то есть число строк равно числу столбцов, матрица A называется квадратной.
оПРЕДЕЛЕНИЕ
2.
Если
матрица имеет m
строк
и n
столбцов,
то она называется матрицей
размера
![]()
Прямоугольная
матрица размера
![]() ,
состоящая из одного столбцаA=
,
состоящая из одного столбцаA=![]() называетсястолбцевой
и
обозначается так
называетсястолбцевой
и
обозначается так
A =
![]() .
.
Прямоугольная
матрица размером
![]() ,состоящая
из одной строки называется строчной
и имеет вид:
,состоящая
из одной строки называется строчной
и имеет вид:
A=
![]() .
.
Иногда cтолбцевая матрица называется вектор-столбцом, а строчная мавтрица - вектор-строкой или оба вида матриц называются просто векторами.
ОПРЕДЕЛЕНИЕ 3. Квадратная матрица A называется диагональной, если все ее недиагональные элементы равны нулю, и имеет вид:
A=
 .
.
Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны единице, называется единичной обозначается символом E :
E= .
.
Матрица A
с элементами aij
называется правой
(верхней),
если
![]() ,
илевой
(нижней)
треугольной,
если aij
= 0
,
илевой
(нижней)
треугольной,
если aij
= 0
![]() .
.
Матрица A
с элементами aij
называется
строго
правой (строго верхней) треугольной,
если
![]() и строго
левой (строго нижней) треугольной, если
aij=0
и строго
левой (строго нижней) треугольной, если
aij=0
![]() .
.
Квадратная матрица, в которой все элементы расположены симметрично главной диагонали, то есть aij= aji (i j) называется симметричной матрицей.
ОПРЕДЕЛЕНИЕ 4. Матрицы A и B называются равными, если они имеют одинаковые размеры и aij= bij i и j. Равенство матриц A и B обозначается так A=B.
Линейные операции над матрицами
К линейным операциям над матрицами относятся: сложение, вычитание и умножение матриц на числа.
ОПРЕДЕЛЕНИЕ 5.
Суммой
матриц A и B размером
mn
называется матрица
С того же
размера, элементы которой
![]() равны
сумме соответствующих элементов
aij
и bij
матриц
A и
B, то есть
C=A+B или
равны
сумме соответствующих элементов
aij
и bij
матриц
A и
B, то есть
C=A+B или
 .
.
Операции сложения матриц коммутативные и ассоциативные, то есть
а)
![]() ,б)
,б)
![]() ,
,
в)
![]() ,
г)
,
г)![]() -
нулевая матрица).
-
нулевая матрица).
Разностью двух
матриц A и B одного и того же размера
![]() называется
матрица
C того же размера, элементы которой равны
разности соответствующих элементов
aij
и bij
матриц A и B, то есть
называется
матрица
C того же размера, элементы которой равны
разности соответствующих элементов
aij
и bij
матриц A и B, то есть
![]() =
aij -
bij
или
=
aij -
bij
или
С=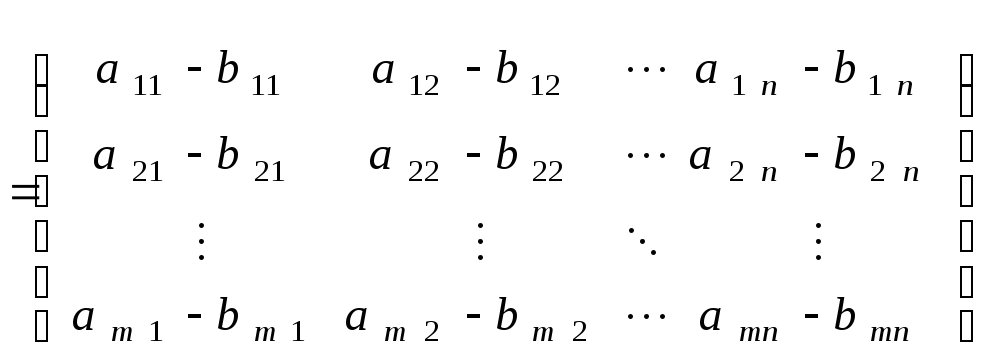
ПРИМЕР. Найти A B, где
 .
.
![]() Имеем
Имеем
![]()

![]()
ОПРЕДЕЛЕНИЕ 6.
Произведением
матрицы A размером mn
на число
называется
матрица,
элементы которой получаются умножением
всех элементов матрицы A на число .
Эта операция обозначается
![]()
C=
·A= .
.
Произведение матрицы A на число подчиняется следующим законам:
а)
![]() б)
б)
![]() в)
, в).
в)
, в).![]() .
.
ПРИМЕР.
Найти 2·
, где A= .
.
![]() Имеем
Имеем
2 · .
ОПРЕДЕЛЕНИЕ 7. Произведением матрицы A размером mn и матрицы B размером пp называется матрица C размером m p, если
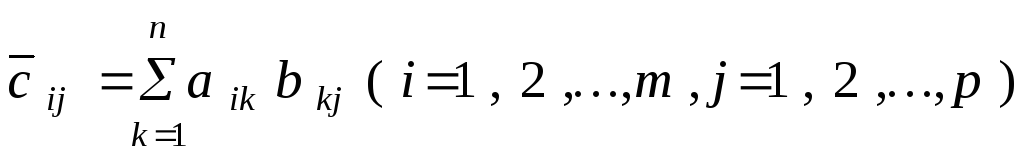 .
.
Из определения
следует, что операция умножения матриц
имеет место тогда и только тогда, когда
число столбцов матрицы A
равно числу
строк матрицы B.
При этом элемент матрицы С вычисляется
по следующему правилу: чтобы
получить элемент
![]() матрицы
, стоящей в i-й строке и j-ом столбце,
нужно элементы i-й строки первой
матрицы
A умножить на соответствующие элементы
j-го столбца второй B и полученные
произведения сложить.
матрицы
, стоящей в i-й строке и j-ом столбце,
нужно элементы i-й строки первой
матрицы
A умножить на соответствующие элементы
j-го столбца второй B и полученные
произведения сложить.
ПРИМЕР.
Найти
A
· B,
где
A=![]() ,
B=
,
B=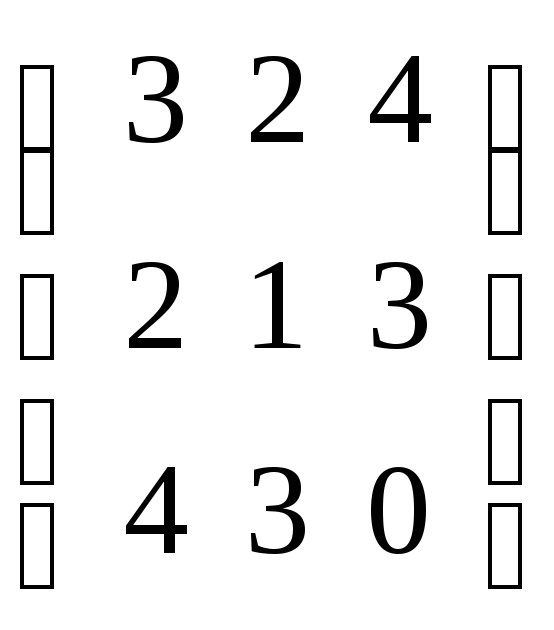 .
.
![]() Имеем
Имеем
A·B=![]() ·
· =
=
![]()
![]()
Если операция произведения матриц выполнима, то она подчиняется следующим условиям:
а)
![]() ;б)
;б)
![]() ;
;
в)
![]() ;г)
;г)
![]() .
.
Следует отметить, что операция произведения двух матриц не обладает свойством переместительности, то есть AB BA .
Выражение вида
An=
называется
n-й степенью матрицы А.
Если A-квадратная
матрица, а n
- целое положительное число, то An=
A ·A ·A ·... ·A.![]()
