2.1.2. Формы записи задачи линейного программирования

Как отмечено выше, среди широкого класса задач опти­мального программирования имеются важные подклассы за­дач, для которых разработаны эффективные методы реше­ния. Наиболее изученным подклассом задач являются зада­чи линейного программирования.

В задаче линейного программирования (ЗЛП) требуется найти экстремум (максимум или минимум) линейной целе­вой функцииf():

max(min) f()=c1x1+c2x2+…+ cnxn,

(2.9)

при ограничениях (условиях):

a11x1+a12x2+…+ a1nxn {}b1,
a21x1+a22x2+…+ a2nxn {}b2,	(2.10)
………
am1x1+am2x2+…+ amnxn {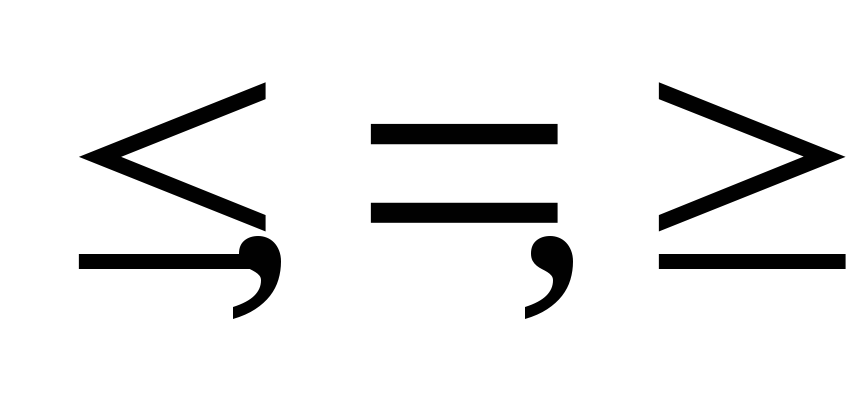}bm,
xj0, j=	(2.11)

гдеa_ij, b_i, c_j (i=,j=)— заданные постоянные величины.

Так записываетсяобщая задача линейного программиро­ванияв развернутой форме; знак{}означает, что в конкретной ЗЛП возможно ограничение типа равенства или неравенства (в ту или иную сторону).

Систему ограничений (2.10) называют функциональны­ми ограничениями ЗЛП, а ограничения (2.11) — прямыми.

Вектор= (х₁, х₂, ..., x_п),удовлетворяющий системе ог­раничений (2.10), (2.11), называетсядопустимым решением, илипланомЗЛП, т.е. ограничения (2.10), (2.11) определяютобласть допустимых решений,илиплановзадачи линей­ного программирования(область определенияЗЛП).

План (допустимое решение), который доставляет максимум или минимум целевой функции (2.9), называется опти­мальным планом (оптимальным решением)ЗЛП.

Канонической формойзаписи задачи линейного програм­мирования (КЗЛП) называют задачу вида (запись с исполь­зованием знаков суммирования):

Найти

max f()=

(2.12)

при ограничениях

	(2.13)
, j=.	(2.14)

Векторная форма записи КЗЛП имеет вид:

Найти maxf()=CX

при ограниченияхA₁x₁+A₂x₂+…+ A_nx_n,= В,

гдеС=(c₁,c₂, ...,c_n),Х=(x₁, x₂,...,x_n),

СХ —скалярное произведение векторовС,Х,

A_jиВ— вектор-столбцы:

,, …,,.

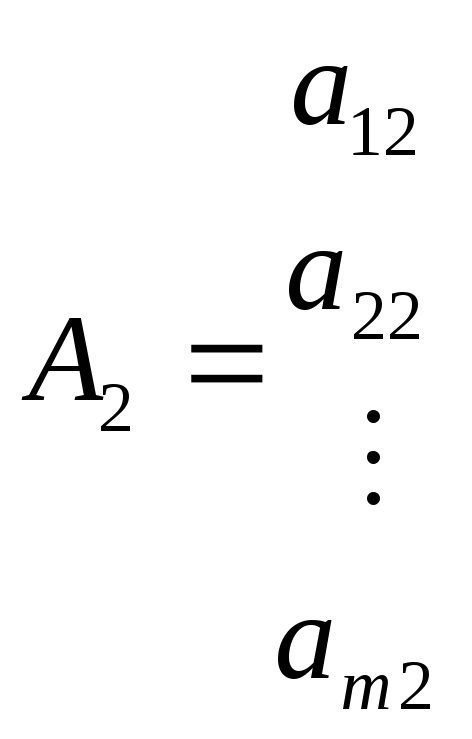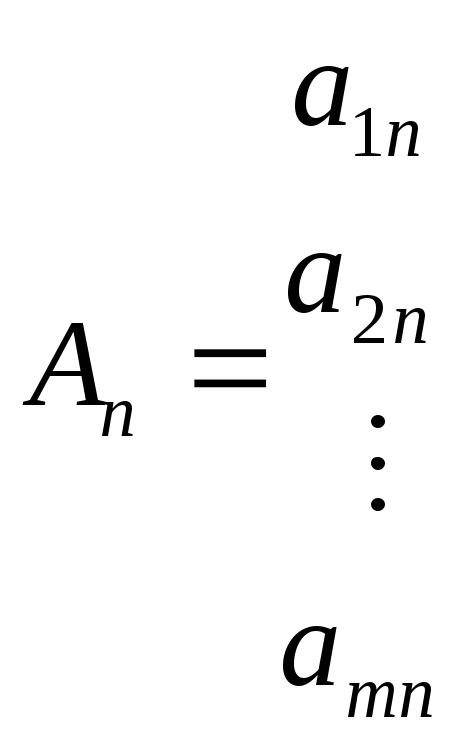Матричная форма записи КЗЛП:

max f()=CX

при условияхAX = B, X0.

ЗдесьС=(c₁, c₂,…, c_n,) —вектор-строка; А=(а_ij)— матри­ца размерноститxп,столбцами которой являются вектор-столбцыA_j,

— вектор-столбец,— вектор-столбец.

Расширенная матрица этой системы будет иметь вид:

=

Иногда используется стандартная форма записи ЗЛП:

max(min)f()=CX,

AXB, X0.

При этом запись X 0понимают как вектор (или век­тор-столбец в зависимости от контекста), у которого все ком­поненты (элементы) неотрицательны.

Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида (2.10) k-ой дополнительной переменной x_n+k 0 со знаком “-“ в случае ограничения типаи знаком “+” в случае ограниче­ния типа.

▼

Пример. Имеется задача линейного программирования

max f()=c1x1+c2x2,

a11x1+a12x2b1,

a21x1+a22x2b2,

xj0, j=

Представим ее в канонической форме

max f()=c1x1+c2x2+0x3+0x4,

a11x1+a12x2+x3=b1,

a21x1+a22x2+x4=b2,

xj0, j=

Расширенная матрица будет иметь вид:

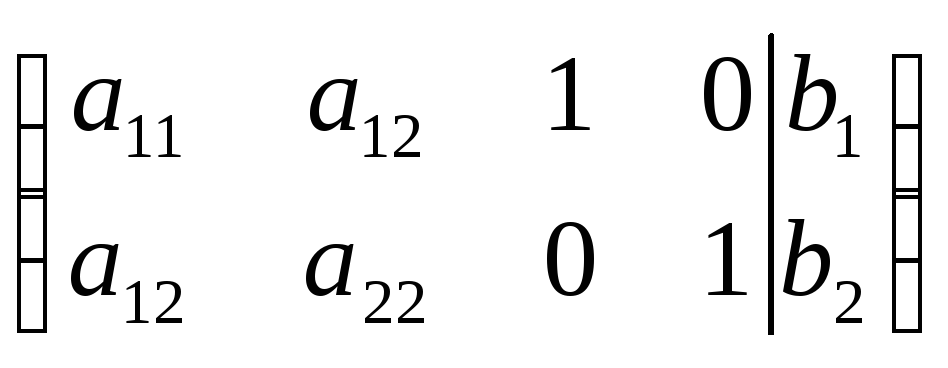
В ее составе присутствует единичная матрица.

▲

Если на некоторую переменнуюх_rне накладывается ус­ловие неотрицательности, то делают замену переменных,,. В преобразованной задаче все переменные неотрицательные. Переход к задаче на макси­мум достигается изменением в случае необходимости знака у целевой функции.

К математическим задачам линейного программирова­ния приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде ин­терпретируются как задачи об оптимальном использова­нии ограниченных ресурсов (задача о раскрое, смесях, дие­те и т.д.).

Изучение и понимание современных экономико-матема­тических методов предполагает достаточно серьезную математическую подготовку экономистов. Для освоения задач и методов в пределах наших занятий необходимы знания ос­новных понятий и элементов высшей математики, матрич­ной и векторной алгебры.