Тема 3. Балансовый метод

3.1. Экономико-математическая модель межотраслевого баланса

Балансовые модели, как статистические, так и динамиче­ские, широко применяются при экономико-математическом моделировании экономических систем и процессов. В осно­ве создания этих моделей лежит балансовый метод, т.е. ме­тод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Если описывать экономическую систему в целом, то под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым отдель­ными экономическими объектами количеством продукции и совокупной потребностью в этой продукции. При таком подходе рассматриваемая система состоит из экономических объектов, каждый из которых выпускает некоторый про­дукт, часть его потребляется другими объектами системы, а другая часть выводится за пределы системы в качестве ее конечного продукта. Если вместо понятия продукт ввести более общее понятие ресурс, то под балансовой моделью следует понимать систему уравнений, которые удовлетворяют требованиям соответствия наличия ресурса и его использо­вания. Кроме приведенного выше требования соответствия производства каждого продукта и потребности в нем, можно указать такие примеры балансового соответствия, как соответствие наличия рабочей силы и количества рабочих мест, платежеспособного спроса населения и предложения товаров и услуг и т. д. При этом соответствие понимается либо как равенство, либо менее жестко — как достаточность ресурсов для покрытия потребности и, следовательно, наличие неко­торого резерва. Важнейшие виды балансовых моделей:

• частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей;

• межотраслевые балансы;

• матричные техпромфинпланы предприятий и фирм.

Балансовый метод и создаваемые на его основе балансо­вые модели служат основным инструментом поддержания пропорций в народном хозяйстве. Балансовые модели на базе отчетных балансов характеризуют сложившиеся про­порции, в них ресурсная часть всегда равна расходной. Для выявления диспропорций используются балансовые модели, в которых фактические ресурсы сопоставлялись бы не с их фактическим потреблением, а с потребностью в них. В связи с этим необходимо отметить, что балансовые модели не со­держат какого-либо механизма сравнения отдельных вари­антов экономических решений и не предусматривают взаи­мозаменяемости разных ресурсов, что не позволяет сделать выбор оптимального варианта развития экономической сис­темы. Этим определяется ограниченность балансовых моде­лей и балансового метода в целом.

Балансовые модели строятся в виде числовых матриц — прямоугольных таблиц чисел. В связи с этим балансовые модели относятся к тому типу экономи­ко-математических моделей, которые называются матрич­ными. В матричных моделях балансовый метод получает строгое математическое выражение.

Простая макроэкономическая модель предполагает наличие всего двух секторов экономики: производители и потребители. От производителей идет поток товаров и услуг, а от потреби­телей - поток денег (рис. 1). При этом товары и услуги можно измерять не в физических объемах, а в текущих рыночных ценах, т.е. в стоимостных объ­емах.

Рис.1

Прямоугольник, обозначенный на схеме как "Производители", включа­ет все многообразие фирм, предприятий и целых отраслей производства, занимающихся активной экономической деятельностью. Всю производи­мую ими продукцию (товары и услуги) удобно разделить на две части: про­межуточный продукт и конечный продукт.

Промежуточный продукт — это та часть совокупного продукта, которой производители обмениваются между собой или используют для собствен­ных нужд. Например, электроэнергия используется практически в любом производстве. В свою очередь, энергетический комплекс нуждается в про­дукции огромного количества отраслей.

Конечный продукт — это вся продукция, предназначенная для потреби­телей.

▼

Пример. Рассмотрим простой пример, поясняющий сказанное. Пусть произво­дители состоят всего из двух фирм: фирма 1 и фирма 2. Предположим, что совокупный продукт, выпускаемый фирмой 1 за год, составляет в стоимо­стных объемах 400. (Это может быть 400 тысяч долларов или 400 миллионов рублей.) Для этого производства используется продукция собственных под­разделений фирмы 1 в объеме 40 и закупленная у фирмы 2 в объеме 320. Аналогичные цифры для фирмы 2 таковы: совокупный продукт - 500, по­ставки собственных подразделений - 100, закупки у фирмы 1 - 200. Таким образом, фирма 1 поставляет самой себе 40 единиц и фирме 2 - 200 еди­ниц. Если из совокупного продукта фирмы 1, равного 400, вычесть эти две величины (промежуточный продукт), то получим конечный продукт, в дан­ном случае равный 160:

400 – 40 - 200 = 160.

Аналогично фирма 2 поставляет самой себе 100 единиц и фирме 1 —320, что дает в сумме промежуточный продукт. Если его вычесть из совокупного продукта фирмы 2, равного 500, то получим конечный продукт:

500 – 100 - 320 = 80.

Полученные результаты можно наглядно представить в виде схемы, изо­браженной на рис. 2.

Рис.2

Здесь стрелками обозначены все стоимостные потоки, а числами вели­чины этих потоков. Числа в прямоугольниках показывают совокупный про­дукт для каждой фирмы. К этому примеру мы будем неоднократно возвра­щаться для иллюстрации общих результатов.

Модель, изложенная выше для простого случая двух фирм-производи­телей, получила название модели "затраты-выпуск", или модели межотраслевого баланса.

Далее удобно перейти к нормированным величинам. Другими словами, к затратам, отнесенными к единице (в стоимостном выражении) продукции. Для нашего простого примера это можно пояснить с помощью таблицы, показанной ниже:

От фирмы	Поставки фирме
	1	2
1	0,1	0,4
2	0,8	0,2

Здесь первый столбец показывает, что для производства единицы про­дукции фирме 1 необходимы поставки от фирмы 1 (самой себе) в размере 0,1, а от фирмы 2 в размере 0,8. Действительно, разделив поставки фирмы 1 самой себе (это 40) на совокупный продукт фирмы 1 (это 400), получаем.

Аналогично для поставок фирмы 2 на единицу продукции фирмы 1 - .

Второй столбец таблицы относится соответственно к поставкам фирме 2 для производства единицы продукции. Еще раз подчеркнем - в стоимост­ном и нормированном выражении.

Если опустить наименования, то таблицу можно представить в виде ма­трицы

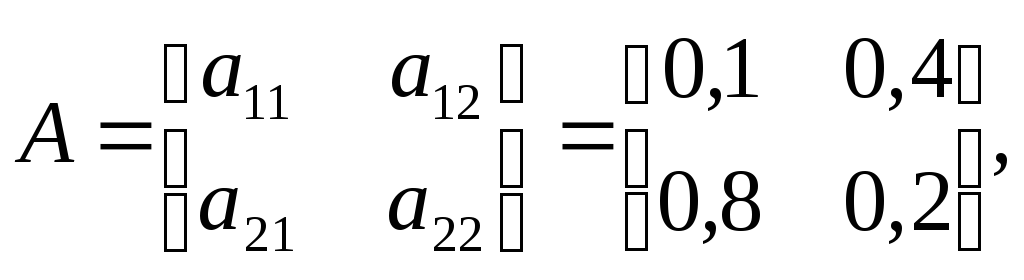
где элементы матрицы а_ij называются коэффициентами прямых материальных затрат (про­изводственными коэффициентами).

Одна из важнейших предпосылок модели "затраты-выпуск" - линейность связей — состоит в том, что выпуск продукции предполагается пропорцио­нальным прямым затратам, т.е. если, например, мы хотим увеличить выпуск вдвое, то необходимо в 2 раза увеличить все затраты. Линейность свя­зей - это, разумеется, упрощение реальной экономической действитель­ности, облегчающее, однако, проведение расчетов. Для нашего простого примера линейность связей означает следующее. Если обозначить совокупный продукт фирмы 1 и фирмы 2 через x₁ и x₂, а конечный продукт — через у₁ и у₂ соответственно, то будем иметь систему линейных уравнений, которая связывает производство на каждой фирме друг с другом и конеч­ным продуктом (спросом)

.

Действительно, если собственные затраты на единицу продукции фирмы 1 составляют 0,1, то для выпуска x₁ продукции они будут 0,1x₁ (линейность связей). Соответственно, если фирма 2 на про­изводство единицы продукции осуществляет закупки у фирмы 1 на 0,4, то для производства количества х₂ эти закупки составят 0,4х_2. Поставки фир­мы 1 самой себе и фирме 2 в сумме с конечным продуктом у₁ как раз и со­ставляют совокупный продукт х₁. Это и есть первое уравнение системы. Рассуждая аналогично, получаем второе уравнение. Эту систему уравнений в матричных обозначениях можно записать в виде

,

или в более компактной форме

,

где А — уже известная нам матрица коэффициентов прямых затрат (т.н. технологическая матрица), а Х и Y— вектор-столбцы совокупного и конечного продуктов соответственно.

▲

В общем случае, когда имеется п отраслей производства, можно ввести матрицу коэффициентов прямых затрат размера п п:

=.

Матрица А является основой экономико-математической модели межотраслевого баланса. Здесь каждый элемент а_ij означает количество затрат промежуточной продукции i-й отрасли для производства единицы продукции в j-й отрасли. Коэффициенты а_ij рассчитываются следующим образом:

,

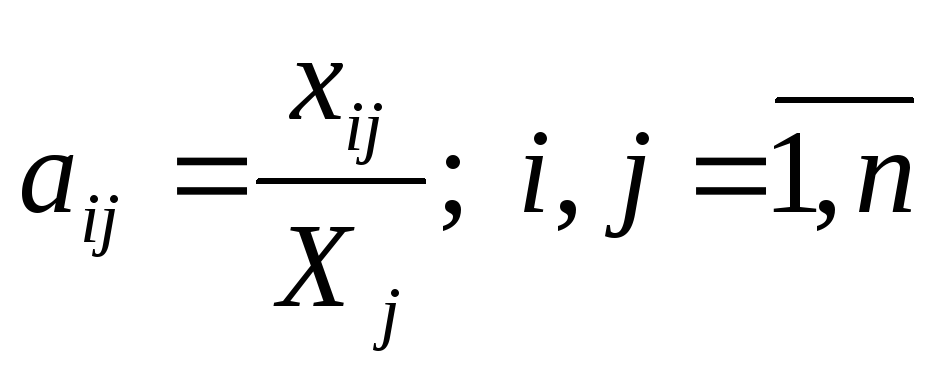(1)

где X_j – валовая продукция j-й отрасли.

Определение 1. Коэффициент прямых материальных за­трат показывает, какое количество продукции i-й отрасли необходимо, если учитывать только прямые затраты, для производства единицы продукции j-й отрасли.

Если определить векторы-столбцы совокупной (валовой) продукции Х и конечной продукции Y как

, ,

где x_i и у_i - соответственно валовая и конечная продукция отрасли i, то система уравнений в матричной форме примет вид

,

(2)

Эта система уравнений называется экономико-математической моделью межотрас­левого баланса (моделью Леонтьева, моделью «затраты— выпуск»). С помощью этой модели можно выполнять три варианта расчетов:

1. Задав в модели величины валовой продукции каждой отрасли (X_i), можно определить объемы конечной про­дукции каждой отрасли (Y_i):

,

(3)

2. Задав величины конечной продукции всех отраслей (Y_i), можно определить величины валовой продукции каждой отрасли (X_i):

,

(4)

3. Для ряда отраслей, задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых, в этом варианте расчета удобнее пользоваться не матричной формой модели (2), а системой линейных уравнений (с учетом (1)):

,

(5)

В формулах (3) и (4) Е обозначает единичную матрицу n-го порядка, а (Е - А)^-1 обозначает матрицу, обратную к матрице (Е - А). Если определитель матрицы (Е - А) не равен нулю, т.е. эта матрица невырожденная, то обратная к ней матрица существует.

Обозначим эту обратную матрицу через В=(Е - А)^-1, тогда систему уравнений в матричной форме (4) можно записать в виде

,

(4`)

Элементы матрицы В будем обозначать через b_ij, тогда из матричного уравнения (4`) для любой i-й отрасли можно получить следующее соотношение:

,

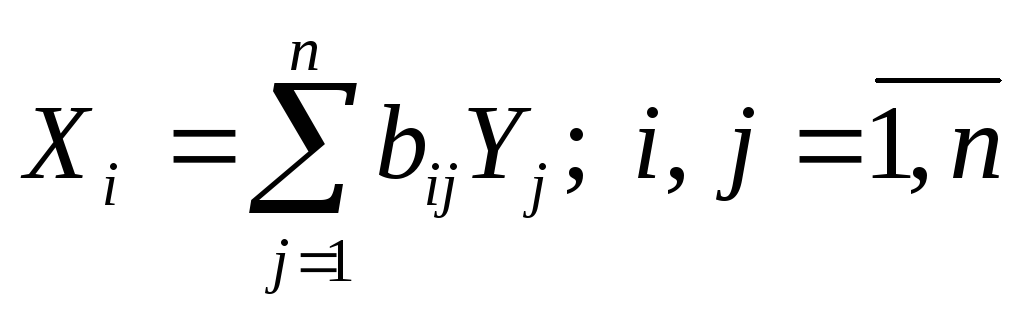(6)

Из соотношений (6) следует, что валовая продукция выступает как взвешенная сумма величин конечной про­дукции, причем весами являются коэффициенты b_ij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования еди­ницы продукции j-й отрасли. В отличие от коэффициентов прямых затрат а_ij коэффициенты b_ij называются коэффици­ентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства.

Определение 2. Коэффициент полных материальных за­трат b_ij показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.

Коэффициенты полных материальных затрат можно приме­нять, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей:

(7)

где и — изменения (приросты) величин валовой и конечной продукции соответственно.

Покажем, как можно использовать уравнение Леонтьева для решения различных задач.

▼

Пример. Пусть требуется определить конечный, продукт каждой отрасли, если известны объемы совокупных продуктов и матрица коэффициентов пря­мых затрат. Для решения достаточно переписать уравнение Леонтьева в виде (или воспользоваться уравнением (3)) и подставить заданные А и X.

В качестве примера рассмотрим случай двух фирм-производителей, когда совокупный продукт фирмы 1 равен 200, а фирмы 2 - 300. В этом случае

и, подставляя в уравнение, сразу находим

Таким образом, конечный продукт фирмы 1 равен 60, а фирмы 2 - 80. Перейдем к более трудной обратной задаче - определению совокупного продукта по известному конечному продукту (конечному спросу). Отметим, что именно эта задача чаще решается на практике, так как в рыночной эко­номике именно спрос задает объемы производства.

Теперь воспользуемся уравнением Леонтьева вида (4).

В ернемся к нашему простому примеру с двумя фирмами-производите­лями. Предположим, что конечный продукт фирмы 1 должен составить 70, а фирмы 2 — 120. Требуется определить необходимый совокупный (валовый) продукт каждой фирмы. Матрица коэффициентов прямых затрат предполагается известной

Для решения находим матрицу

и вычисляем для нее обратную матрицу (т.е. коэффици­енты полных материальных затрат)

,

Мы воспользовались формулой для вычисления обратной матрицы раз­мера 2х2.

Теперь, подставляя в формулу заданный век­тор-столбец конечного продукта Y, находим

Таким образом, чтобы удовлетворить конечный спрос, совокупный про­дукт фирмы 1 должен составить 260, а фирмы 2 - 410.

Отметим, что самая трудоемкая часть задачи - это вычисление обратной матрицы (Е- А)^-1, (т.е. коэффици­ентов полных материальных затрат) если учесть, что ее размер в реальных задачах может достигать нескольких сотен. Однако когда эта матрица найдена, расчет раз­личных вариантов представляет собой сравнительно простую процедуру. Например, предположим, что в последнем примере конечный продукт фир­мы 1 равен 60, а фирмы 2 -80, то, используя ранее вычисленную матрицу коэффици­ентов полных материальных затрат легко находим

Таким образом, для удовлетворения последнего варианта конечного спроса совокупный продукт фирмы 1 должен быть 200, а фирмы 2 - 300.

▲

В заключение отметим, что в реальных задачах приходится иметь дело не с двумя фирмами, а с сотнями отраслей производства. Решение таких задач немыслимо без использования компьютеров и соответствующего про­граммного обеспечения