
шПОРЫ ПО ФИЗИКЕ НА ЭКЗАМЕН
.docx|
1 БИЛЕТ Процесс взаимодействия энергии, происходящей в поле катушки 1) В цепи соединяющей индуктивность и емкость, могут возникать электрические поля. Присоединим отключенный от индуктивности конденсатор постоянного напряжения. Это приведет к возникновению на обкладках разноименных зарядов +q и –q. Между обкладками возникает электрическое поле. Энергия равна q2/2C. Если затем отключить источник напряжения и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия поля будет уменьшаться, но зато возникает все возрастающая энергия материального поля, обусловленного током, текущим через индуктивность. Эта энергия равна LC2/2. Поскольку активное сопротивление контура равно нулю, то полная энергия, слагающаяся из энергий электрического и материального полей не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе достигнет нуля и энергия электрического поля равна нулю, энергия материального поля, а значит и ток, достигают наибольшего значения. В дальнейшем ток уменьшается, и когда заряды на обкладках достигнут первоначального значения q, сила тока станет равной нулю, затем эти же процессы происходят в обратном направлении, после чего система приходит в исходное состояние и цикл повторяется вновь. Электрическое и материальное поля не могут возникать в контурах из конденсатора и резистора или из катушки индуктивности и резистора, т.к. предполагается что электрическое поле сосредоточено в конденсаторе, а магнитное в катушке индуктивности. Для возникновения электромагнитных колебаний необходимы конденсатор и катушка способные запа-ть энергией. |
1 БИЛЕТ 2) Под действием внешнего поля диэлектрик поляризуется. Это означает, что дипольный момент диэлектрика становится не равным 0. В качестве величины, характеризующей степень поляризации диэлектрика, берут дипольный момент единицы объёма. Если поле или диэлектрик неоднородны, степень поляризации в разных точках диэлектрика будет различна. P=∑P/∆V – поляризованность диэлектрика. У изотропных диэлектриков поляризованность связана с напряженностью соотношением P=λε0E , где λ диэлектрическая восприимчивость диэлектрика. Для диэлектриков, построенным из неполярных молекул : в предел ∆V попадает количество молекул, равное n∆V, где n число молекул в единице объёма. P=βε0E => ∑P∆V=n∆Vβε0E. Под действием внешнего магнитного поля заряды в неполярной молекулы смещаются друг относительно друга: положительные по направлению поля, отрицательные против поля. В результате молекула приобретет дипольный момент, величина φ пропорциональна направленности поля. Этот процесс называется электронной поляризацией и происходит в неполярных диэлектриках. Действие внешнего поля на полярные молекулы сводится в основном к стремлению повернуть молекулы так, чтобы её дипольный момент установился по направлению поля. На величину дипольного момента внешнее поле практически не влияет => полярная молекула ведёт себя во внешнем поле как жесткий диполь. В случае диэлектриков ориентирующему действию внешнего поля противится тепловое взаимодействие молекул. Диэлектрическая восприимчивость диэлектриков обратно пропорциональна абсолютной температуре, т.к P= λε0E, то P обратно T.
|
2 БИЛЕТ 1) Работа выхода: В металлах свободные электроны могут перемещаться внутри него между узлами кристаллической решетки. В качестве своба выступают валентные е. W=Wк+Wпот Wпот<0 (т.к. притяжение) Wк>0 если [Wпот]>[Wк], то е не может покинуть металл, т.к. ν=(3kT/m)1/2, ν~106м/с Если [Wпот]<[Wк] , то е может вылететь. При вылете е остается дырка, е может туда вернуться , но наиболее быстрые е не возвращаются , т.е. вблизи поверхности металла на расстоянии 10-10 м образуется двойной электрический слой. Wпот=0 при Т≠0 К. Даже при Т=0 К е в атоме металла не находится на дне потенциальной дамы в силу волновых свойств тока. Энергия, которой обладает е при Т=0 К – Энергия Ферми Wк. С увеличением температуры энергия Ферми практически не меняется. Минимальная энергия, которую нужно сообщить е, чтобы перевести из металла в вакуум, называется работой выхода. Т.к. Wпот<0, то выход означает повышение Wпот до 0 [Авых=eU] . Термоэлектронная эмиссия – вырывание е из металла при нагревании. Если энергия теплового движения е равна Wтепл=3kT/2 , то энергия, необходимая для вырывания е соизмерима с Wтепл. W= Wпот-Wк => Wтепл при Т≈15000 К. Вырывание происходит при 1000-3000 К. Скорость при этом изменяется от min до max. Эмиссию легко наблюдать в вакуумном диоде. Катод нагревают до 1000-9000 К. Вблизи катода образуются электронные облака, и если прижито анодное направление UA, то возникает направленное движение е и потечет электрический ток. Сам вакуум не проводит электрический ток. Для е при столкновении ионов в металле. В вакууме же е не испытывают столкновений, поэтому зависимость силы анодного тока от U не линейная IA=CU3/2 Закон Богуславского Ленгмюра В вакууме Iн (ток насыщения) зависит от температуры катода. При увеличении температуры Iн растет, это объясняется увеличением эмиссии электронов, т.е. количеством вырываемых с поверхности катода электронов в единицу времени равно количеству е, достигших анода за то же самое время. С не зависит от температуры катода, а зависит от материала катода и чистоты его поверхности.
|
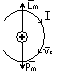
2 БИЛЕТ 2) Магнитный момент атома По Бору атом- положительно заряженное ядро ( состоящее из протонов и нейтронов). I=eυ Круговой ток создает магнитный момент (который определен по правилу правого винта). Pm=IS=eυπr2
Lm=mvr-орбитальный механический момент
=> Pm/Lm=-eυπr2/ mvr=- eυ2πrr/2mvr=-e/2m (‘-‘ означает
противоположно направленные Pm и Lm) .
Отличие магнитного момента, связанного
с орбитальным движением электрона, к
механическому моменту -величина
постоянная и не зависит ни от радиуса
отбиты ни от скорости его движения –
это гиромагнитное отложение. Собственный
механический момент е называется
спином. Суммарный магнитный момент
атома определяется орбитальным
магнитным моментом, спиновым магнитным
моментом и магнитным моментом ядра.
Рат=Рm+Рs+Ря, но т.к. mя>>mе и Ря>>Ре,
то в основном Рат=Рm+Р. Включим внешнее
магнитное поле. На заряд действует
сила Лоренца Fл=evB. Т.к. е движутся вокруг
ядра, то между е и ядром возникает сила
притяжения , которая обуславливает
его центростремительное ускорение.
F=ma(*)=e2/4πε0r2, εί=-dФ/dt=-SdB/dt=-πR2dB/dt=-E2πR
E=rdB/2dt. Т.к. F=eE=evdB/2dt, то (*)Fdt=d(mv)=mdv
mdv=erdB/2. Т.к. v=ωR, то rdω=erdB/2m => dω=ed/2m;
∆ω=-e∆B/2m-частота нарморовой процессии.
|
3 БИЛЕТ 1) Уединенный проводник – проводник, который удален от других проводников, тел и зарядов. Его потенциал:φ=q/4πε0r. Из опыта известно, что различные проводники, будучи одинаково заряженными, имеют различные потенциалы, т.е. q=Cφ. Величину C=q/φ называют электроемкостью. Ёмкость определяется зарядом, сообщенному проводнику и изменяет его потенциал на единицу. Ёмкость проводника зависит от его размеров и формы и не зависит от материала. Если к заряженному проводнику приблизить другой проводник, внутри них возникают индуцированные заряды, причём ближайшими к проводнику заряду q будут заряды противоположного знака. Эти заряды ослабляют поле, создаваемое зарядом q, т.е. снижают потенциал проводника, что приводит к повышению его электроемкости. Потенциал заряженного шара радиуса R, находящегося в однородной среде, с диэлектрической проницаемостью ε, равен φ=q/4πεε0R => q=4πεε0Rφ [C]= 2) Взаимная индукция. возьмем два контура 1 и 2. Первый контур создает через контур два магнитный поток Ф2=L21I1. При изменении тока I1 в контуре 2 индуцируется ЭДС ε12=- L21dI1/dt Аналогично Ф1=L12I2; ε21=- L12dI2/dt. Контуры 1 и 2 называют связанными. Коэффициенты проницаемости L12 и L21 называют взаимной индуктивностью контуров. Их величины зависят от формы и размеров L12=L21. Взаимное расположение контуров, а также от магнитной проницаемости окруж. контуры средн. через коэффициент взаимной индукции контуров выражается взаимная энергия W12: W12=L12I1I2.
|
|
4 БИЛЕТ 1) Напряженность – сила, с которой поле действует на малый положительный заряд, внесенный в это поле. Это силовая характеристика поля: Е=F/q. Потенциал- энергетическая характеристика, которая численно равна работе , которую совершают силы поля над положительным зарядом при удалении его из данной точки в бесконечность. A∞=qφ => φ=A∞/q. φ=q/4πε0α, A=q∆φ, => φ численно равен W/q. Связь между потенциалом и напряженностью такая же, как и связь между силой и работой: dA=Fdℓ=Eq0dℓ. dA=φq0-q0 (φ+dφ)=-q0dφ. E=-dφ/dℓ=-q∞dφ. Градиентом скалярной величины называется вектор, направленный в сторону возрастания этой величины и численно равный скорости изменения этой величины. grad φ противоположен по направлению вектору напряженности. Поверхность одинакового потенциала называется эквипотенциальной поверхностью. При перемещении по эквипотенциальной поверхности потенциал не меняется (dq=0) Следовательно касательная к поверхности составляющая вектора E=0 => вектор Е в каждой точке направлен по нормали к эквипотенциальной поверхности. 2) Теория Био-Савара-Лапласа. B~I. Предположим, что магнитная индукция – векторная величина и магнитная индукция подчиняется принципу суперпозиции магнитный полей: B=∑Bi. Idℓ - элемент тока, расстояние от которой до точки А равно v, α-угол между элементом тока и направлениями на точку. dB=μIdℓsinα/4πr2- закон Био-Савара-Лапласа.
|
5
БИЛЕТ 1)
2) Если проводник поместить в электрическое поле он начнет перемещаться под действием силы Ампера: F=ℓIBsina, где a- угол между I и dℓ, dF=dℓIBsina. Направление силы Ампера определяется правилом левой руки: 4 пальца вдоль направленных силовых линий магнитное поле в ладонь, то большой палец укажет направление силы Ампера dF=I[dℓB]. Работа по перемещению проводника с током: dF=dℓIBsina(dℓB) sin(dℓB)=1 тогда F=ℓIB dA=Fdx => A= ℓIB∫(0,x)dx=IBℓx=ISB=I∆Ф. где ∆Ф-изменение потока, возникшего вследствие перемещения проводника в магнитном поле. Работа совершается за счет ε источника.
|
6
БИЛЕТ 1)Потенциальность электрoстатистического
поля. рассчитаем работу при перемещении
заряда q1 в поле, создаваемом зарядом
q при переходе из точки 1 в точку 2.
A=-dlcosa. dlcosa=dr=> Fdr=q1qdr/4πε0r2 =>
A=∫dA=∫q1qdr/4πε0r2=-q1q2/4πε0r==-q1q2(1/r1-1/r2)/4πε0
=> работа при перемещении электрического
заряда q1 в поле заряда q не зависит от
выбора пути, а определяется лишь
начальным и конечным положением
перемещения по среде => электрическое
статистическое поле потенциально.
A132=A14. А132=-А241 Апол=А3241=0 => работа
перемещения зарядов в электрическом
поле dA=!. Если q:1=F/q, то dA=Rdlcosa=(E^dl); A=
2) Всякий реальный контур обладает активным сопротивлением. Энергия, запасённая в контуре, постепенно расходуется на нагревание и колебания затухают. По закону Ома R=φ1-φ2=ε12, где φ1 φ2 =-q/C ε12=-LdI/dt. IR=-q/C-dv/dt. Разделив уравнение на L и заменив I=q′,dI/dt=q′, получим q′′+Rq′/L+q/LC=0, т.к. ω02=1/LC, β=-LdI/dt, получим q′′+2βq′+ω02q=0 – дифференциальное уравнение затухающих колебаний. При условии, что β2<a, -ex2/4L2=1/4C. решение примет вид q=qme-βtcos(wt+a), где w=(w02-β2)1/2 частота затухающих колебаний меньше собственной частоты w. U=Ume-βtcos(wt+a) I=w0qme-βtcos(wt+a+ψ), где sin ψ=w/(w2+β2)1/2=w/w0,cosψ=-β/ (w2+β2)1/2=-β/w0 Полная система дифференциальных уравнений Максвелла в дифференциальной форме wt*E=-∂β/∂t; divD=P; wtH=j+∂D/∂t;div B=0. Уравнение Максвелла – наиболее общее уравнение для электрических и магнитных полей в покоящихся срезах. Если заряды и токи непрерывно распределены в пространстве, то обе формы уравнений Максвелла эквиваленты. Сила тока определяется по фазе. Амплитуда убывает по закону е-βt . Логарифмический декремент затухания λ=a(t)/a(t+T)=βT( где a(t) – амплитуда соответствующей величины) – обратен числу колебаний Ne, совершаемых за время, в течение которого амплитуда уменьшается в е раз.λ=1/Ne. λ=βТ=R2π/2Lw= Rπ/Lw. Частота w => и λ определяются параметрами контура L,C и R => логарифмический декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний.
|
7
БИЛЕТ 1) Электрический диполь – система
двух одинаковых по величине, но
противоположных по знаку зарядов,
расположенных на малом расстоянии
друг от друга. p=qℓ, гдеℓ- плечо диполя.
Р направлен по оси диполя от отрицательного
заряда к положительному. q+=q- => E+=E-,
по принципу суперпозиции
Eн=Е-+Е+. 2)Явление самоиндукции IS=φ(направление винта). Если меняется сопротивление то меняется сила тока, меняется магнитный поток. A=Винд:dФ/dt. то в самом контуре, по которому меняется ток, возникает ток индукции. Если значение тока увеличивается:dI/dt>0, то увеличивается магнитный поток (dФ/dt>0), тогда ток самоиндукции направлен так, чтобы препятствовать нарастанию тока (εsi<0) Если dI/dt<0, то dФ уменьшается и убывающий поток обуславливает появление индуцированного тока(εsi>0). Т.к. Ф~В, а В~I, то Ф~I, => Ф=LI, где L- коэффициент самоиндукции (индуктивность). Если ток в контуре равен –LR, то индуктивность численно равна магнитному потоку, пронизывающему этот контур [L]=Гн. Индуктивность зависит от размеров и формы контура, от магнитных свойств среды, в которой расположен контур. H=nI, напряженность поля и оси соленоида (n – число витков на единицу длины). B=μμ0H=μμ0nI ψ=ФN (потокосцепление). N=nℓ. ψ=BSN=μμ0nISnℓ=μμ0n2ISℓ. L=μμ0nV => индуктивность зависит от геометрических размеров и свойств среды. εsi=-dФ/dt, Ф=LI => εsi=-LdI/dt. Ток при размыкании In=I0e-Rt/L, ток при замыкании Is=I0(1-e-Rt/L). Коэффициент τ=L/R называется временем релаксации, это время, в течение которого сила увеличивается в е раз |
8 БИЛЕТ 1)Электрический заряд элементарная частица – количественная мера ее электромагнитного взаимодействия с другими частицами. Всякий заряд образуется совокупностью элементарных зарядов, он является целым кратным е: q=±Ne. Величина заряда измеряется в различных инерциальных системах отсчета оказывается одинаковой => не является релятивистки инвариантным, т.е. величина заряда не зависит от того движется он или покоится. Электрические заряды могут исчезать и возникать вновь. Всегда возникают и исчезают 2 элементарных заряда противоположных знаков. Нейтрон и позитрон при встрече превращаются в нейтральные гамма-фотоны. При этом исчезают заряды +е и –е. В ходе процесса, называемого рождением пары, гамма-фотоны, покидают поле атомного ядра, превращаются в частицы – электрон и позитрон. Т.е. суммарный заряд электрически изолированоой системы не меняется – это закон сохранения электрического заряда. 2)Энергия, запасённая в контуре, постепенно расходуется на нагревание., вследствие чего колебания затухают. Закон Ома: IR=-q/C-LdI/dt – разделив на L и заменив I через q′, а dI/dt через q′′, получим q′′+R q′/L+q/LC, ω02=1/LC, β=R/2L, => q′′+2βq′+ω02q=0 – дифференциальное уравнение затухающих колебаний. При условии β2<<ω02, т.е. R2/4L2<1/LC решение уравнения имеет вид q=qme-βtcos(wt+a), где w=(w02-β2)1/2; w=(1/LC- R2/4L2)1/2 => частота затухающих колебаний w меньше собственной частоты колебаний w0. Логарифмический декремент затухания x=lna(t)/a(t+τ)=βτ, где a(t)- амплитуда соответствующей величины. Декремент затухания обратен числу колебаний Ne, совершаемых за время, в течение t амплитуда уменьшается в e раз. x=1/Ne. Заменив T через 2π/ω => λ=R2π/ω2L= Rπ/ωL => λ определяется параметрами контура β=R/2L называется коэффициентом затухания. T=1/ω=1/(1/LC- R2/4L2)1/2
|
|
9 БИЛЕТ 1) Диэлектрики – вещества, в которых нет свободных электрических зарядов. Диэлектрик состоит из атомов и молекул и в целом электрически нейтрален. Диэлектрики бывают неполярными (центры тяжести “+” и “-“ зарядов находятся в одном месте),напримерCH4, и полярными (центры тяжести не совпадают), например H2О. Рассмотрим электрическое поле между обкладками конденсатора, если в него внести диэлектрик. Е0 – поле, создаваемое свободными зарядами на металлических пластинах (внешнее поле). Во внешнем поле диэлектрик поляризуется. Е′- электрическое поле, создаваемое связанными зарядами. Е=Е0+Е′ векторно или Е=Е0-Е′=Е0-ύ/ε0=Е0-pm/ε0= Е0-λnε0E/ε0= Е0-λnE. E+λnE =Е0=E+æE; 1+æ=ε, E0=εE => ε= E0/E- величина, указывающая во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике, называются диэлектрической проницаемостью. Линии напряженности электрического поля на границе диэлектриков претерпевает разрыв E1=E0/ε1 E2= E0/ε2 D=εε0E – вектор электрического смещения (Кл/м2). Теорема Гаусса: Ф=∑qi – поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности сторонних зарядов.
|
9 БИЛЕТ 2) Термоэлектронная эмиссия- вырывание электронов из металла при его нагревании. В металле имеются валентные е, которые выступают в роли свободных е. Во втором случае притяжение со стороны ионов Wпот<0 (т.к. притяжение), Wкин=mv2/2>0. Если [Wпот]>[Wкин], то е не может покинуть металл. Если [Wкин]>[Wпот], то е способен вылететь, при этом в металле остается дырка, е может вернуться туда, но наиболее быстрые не возвращаются, т.е вблизи поверхности металла образуется двойной электрический слой. Wпот=0 при Т≠0 К. Даже при Т=0 К е в атоме металла не находится на дне потенциальной дамы в силу волновых свойств тока. Энергия, которой обладает е при Т=0 К – Энергия Ферми Wк. С увеличением температуры энергия Ферми практически не меняется. Минимальная энергия, которую нужно сообщить е, чтобы перевести из металла в вакуум, называется работой выхода. Т.к. Wпот<0, то выход означает повышение Wпот до 0 [Авых=eU] . Термоэлектронная эмиссия – вырывание е из металла при нагревании. Если энергия теплового движения е равна Wтепл=3kT/2 , то энергия, необходимая для вырывания е соизмерима с Wтепл. W= Wпот-Wк => Wтепл при Т≈15000 К. Вырывание происходит при 1000-3000 К. Скорость при этом изменяется от min до max. Эмиссию легко наблюдать в вакуумном диоде. Катод нагревают до 1000-9000 К. Вблизи катода образуются электронные облака, и если прижито анодное направление UA, то возникает направленное движение е и потечет электрический ток. Сам вакуум не проводит электрический ток. Для е при столкновении ионов в металле. В вакууме же е не испытывают столкновений, поэтому зависимость силы анодного тока от U не линейная IA=CU3/2 Для е при столкновении с ионами в металле и вакууме е не испытывает столкновений и зависимость силы тока от напряжения нелинейная IA=CUA3/2 – закон Богуславского-Ленгмюра. Iнас зависит от температуры катода, при повышении температуры этот ток растёт, это объясняется увеличением эмиссии электронов. При Iнас количество вырванных с поверхности катода электронов в единицу времени равно количеству е, достигших анода за о же самое время, е не зависит от температуры катода, а зависит от материала катода и частоты его поверхности.
|
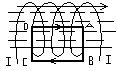
10 БИЛЕТ 1)Под Действием внешнего электрического поля заряды в неполярной молекуле смещаются друг относительно друга. Положительные по направлению поля, отрицательные против поля. В результате частица приобретает дипольный момент, причём P=βε0E, где Р – дипольный момент, β – поляризованность молекулы. Процесс поляризации неполярной молекулы протекает ток, как если бы “+” и “-“ заряды молекулы были связаны друг с другом упругими силами. Поэтому неполярная молекула ведет себя как упругий диполь. Действие внешнего поля на полярные молекулы сводится в основном к стремлению повернуть тк, чтобы её дипольный момент установился по направлению поля. Поляризованная молекула ведёт себя как жёсткий диполь. В качестве величины, характеризующей степень поляризации диэлектрика берут дипольный момент единицы объёма. P=∑P – поляризованность диэлектрика P=λε0E, где λ – диэлектрическая восприимчивость диэлектрика (безразмерная величина). 2)Рассмотрим
соленоид длиной l, имеющий N витков,
по которому течет ток. Бесконечно
длинным считается соленоид, длина
которого во много раз больше, чем
диаметр его витков. Поле такого
соленоида сосредоточено целиком
внутри него. Выберем замкнутый контур
ABCDA.
|
11 БИЛЕТ 1)Теорема Гаусса. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑qi/ε0. Напряженность поля бесконечно заряженной поверхности: под поверхностной плотностью заряда δ понимают заряд приходящийся на единицу поверхности δ=q/S (Кл/м2). Размеры поверхности >> расстояния, на которую рассчитывается напряженность – бесконечная поверхность. Поток через вспомогательную цилиндрическую поверхность, образующие которой параллельны линиям напряженности. N=Nбок+2Nосн=ESбок*сosπ/2+2ESосн*cos0=2ESосн. Из теоремы Гаусса N=∑qi/ε0 => ∑qi/ε0=2Eосн => Е=∑qi/∑Еоснε0=δ/2ε0 Для двух поверхностей – (+) – (-)
2)Если магнитный момент Pm атомов равен 0, то вещество является парамагнетиком. Магнитное поле стремится установить магнитные моменты атомов вдоль В, тепловое движение стремится разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация моментов вдоль поля тем больше, чем > В, и тем меньше, чем выше температура. λкм=С/T – закон Кюри, где С-постоянная Кюри, зависящая от рода вещества, λкм – восприимчивость парамагнитного вещества. С=μ0NAPm2/3k, тогда λкм μ0NAPm2/3kT. Здесь предполагается, что PmB<<kT. В очень сильных полях и при низких температурах наблюдается отступление от пропорциональности между намагниченность парамагнетика I и напряженностью поля Н, в частности, может наступить состояние магнитного насыщения, при котором все Pm выстраиваются поп полю и дальнейшее увеличение Н не приводит к увеличению I. |
12 БИЛЕТ 1)Теорема Гаусса. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑qi/ε0. Напряженность поля бесконечно заряженной поверхности: под поверхностной плотностью заряда δ понимают заряд приходящийся на единицу поверхности δ=q/S (Кл/м2). Размеры поверхности >> расстояния, на которую рассчитывается напряженность – бесконечная поверхность. Поток через вспомогательную цилиндрическую поверхность, образующие которой параллельны линиям напряженности. N=Nбок+2Nосн=ESбок*сosπ/2+2ESосн*cos0=2ESосн. Из теоремы Гаусса N=∑qi/ε0 => ∑qi/ε0=2Eосн => Е=∑qi/∑Еоснε0=δ/2ε0 Для двух поверхностей – (+) – (-)
2)Магнитная
взаимоиндукция параллельных токов.
F
|
|
13 БИЛЕТ 1) dA=-dW А=qq1/ 4πε0r1-qq2/ 4πε0r2 =-∆W W1=qq1/ 4πε0r1 W2= qq2/ 4πε0r2 Величина φ=W/q называется потенциалом поля и численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. φ=q/4πε0r => A=(q1(φ2-φ1). Потенциал является энергетической характеристикой поля, Е – силовая характеристика. φ=А∞/q0, т.к. потенциал равен работе, которую совершили силы поля над единичным положительным зарядом при удалении его из данной точки в ∞. Связь между потенциалом и напряженностью такая же, как и связь между силой и работой dA=-Fdl=qEdl, dA=φq0-qd(φ+dφ)=-q0dφ => Edl=-q0dφ , E=-dφ/dl=-gradφ – взаимосвязь между напряженностью и потенциалом. Градиентом скалярной величины называется вектор, направленный в сторону возрастания этой величины и численно равный скорости изменения этой величины. Градиент φ противоположен по направлению вектору напряженности. Поверхность одинакового потенциала называется эквипотенциальной поверхностью. 2)
Уравнения Максвелла: I:
|
15 БИЛЕТ 1) Для равновесия зарядов на проводнике необходимо выполнение следующих условий: 1) Напряженность поля внутри проводника равна нулю Е=0, это означает, что потенциал внутри проводника должен быть постоянным (φ=const0. 2) Напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормалям поверхности. Если проводящему телу сообщить заряд q, то он распределится так, чтобы соблюдались условия равновесия. Возьмем произвольную замкнутую поверхность, полностью заключенную в пределах тела. При равновесии зарядов поле в каждой точке внутри проводника отсутствует, поэтому поток вектора электрического сменщения через поверхность равна нулю. Согласно теореме Гаусса сумма зарядов внутри поверхности также равна нулю, при равновесии ни в каком месте внутри проводника нет избыточных зарядов – он распределяется по поверхности проводника с некоторой плотностью δ. Возьмём цилиндрическую поверхность, образованную нормалями к поверхности проводника и основаниями dS. Поток вектора электрического смещения через внутреннюю часть поверхности равен 0, т.к. внутри проводника D и Е=0. Вне проводника в непосредственной близости к нему напряженность направлена по нормалям к поверхности. Поэтому для выступа наружу боков поверхности цилиндра Dn=0, а для внешнего основания Dn=D => поток смещения через рассматриваемую поверхность равен DdS. Внутри цилиндра содержится сторонний заряд δdS/δ – плотность заряда в данном месте поверхности проводника. По теореме Гаусса получим: DdS=δdS, т.е. δ=D => E=δ/ε0ε Плотность зарядов при данном потенциале проводника определяется кривизной поверхности – она растет с ростом положительной кривизны (выпуклости). особенно велика бывает плотность зарядов на остриях. Рассмотрим поверхность такой формы. на больших расстояниях от проводника эквипотенциальные поверхности имеют форму сферы, По мере приближения к проводнику. Вблизи выступов эквипотенциальной поверхности располагаются => напряженность поля здесь больше => плотность зарядов на выступах
|
15
БИЛЕТ 2) Если в проводнике создать
электрическое поле и не принять мер
для его поддержания, то перемещение
носителей тока приведёт к тому, что
поле внутри проводника исчезнет и ток
прекратится. Чтобы поддержать ток,
надо от конца проводника с меньшим
потенциалом непрерывно отводить
приносимые сюда током заряды, а к концу
с большим потоком непрерывно их
подводить. Циркуляция вектора
напряженности электростатического
поля равна 0. Поэтому в замке цепи
наряду с участками, на + положительные
носители движутся в сторону убывания
φ, должны иметься участки, на которых
перенос положительных зарядов
происходит в направлении возрастания
φ, т.е. против сил электростатического
поля. Перемещение носителей на этих
участках возможно лишь с помощью сил
неэлектростатического происхождения,
называемых сторонними. Сторонние силы
можно охарактеризовать работой ,
которую они совершают над перемещающимися
в цепи зарядами. Величина, равная
работе сторонних сил над единичным
положительным зарядом, над электродвижущей
силой. (ЭДС) ε=Аст.q. Fст =E′q, где E′ -
напряженность сторонних сил.
Аст=∫Fстdl=й∫E′вд – падение на q. Для
замкнутой цепи ε=
|
16 БИЛЕТ 1)Теорема Гаусса. Е поля для бесконечного цилиндра. Поток вектора напряженности электрического тока через замкнутую поверхность равен алгебраической сумме зарядов, охваченных этой поверхностью, отнесенных к электрической постоянной N=∑qi/ε0. E=F/q, E=q/4πε0r2, - для точечного заряда. Для системы точечных зарядов Е=∑Еi, силовые линии показывают на направление сил. густота определяет модуль Е, N=EnS – число линий. Ионизирующая поверхность перпендикулярна силовым линиям. или N=EScos(n^E). dN=EndS- элементарный поток. τ=q/ℓ- линейная плотность заряда. Построим вспомогательный цилиндр, высота которого равна H, а радиус r. Точка А находится на вспомогательной поверхности, а образующая параллельна оси заряженного цилиндра. N=Nбок+2Nосн, Nосн=0 => N=Nбок=ESбокcos(n^E)=0, cos0=0 => N=ESбок; Sбок=2πh => N=E2πrh т.к. N=∑qi/ε0,то [E=∑qi/2πrhε0=τ/2πrε0] => напряженность поля безименного цилиндра нгеоднородно и является величиной, обратно зависящей от расстояния E=f(1/v). Eвнутр.=0 2)Ток смещения. Изменяющееся во времени магнитное поле вызывает появление эл. п
|
17 БИЛЕТ 1) Энергетическая система точечных зарядов, заряженного конденсатора, проводника электрического поля. Считается, что потенциальная энергия на бесконечности равна 0, а изменение потенциальной энергии равно работе сил электрического поля, кроме того считается, что q1 неподвижен, а q2 движется из ∞ в точку удаленную от q1 на r12. A2=q2(0-φ2)= [q2φ2], где φ1 – потенциал точки поля, куда перемещен 2 заряд φ2=q2/4π ε0r12,A2=q1q2/4π ε0r12. Работа по перемещению 1 заряда : A1=q1(0-φ1)= -q1φ1, φ1=q1/4π ε0r12,A2=q1q2/4π ε0r12.=> A1=A2; W12=A1=A2=(q1φ1+q2φ2)/2. Внесем заряд q3, приближая его из ∞ в точку на расстояние r13 и r23. Работа по перемещению 3 заряда: A=A1+A3=A2+A3= q1q2/4π ε0r12+q3(q1q2/4π ε0r13+ q1q2/4π ε0r23)=4/4πε02(q1(q2/r12+q3/r13)+q2(q1/r12+q3/r13)+q3(q1/r13+q2/r23))1/2[q1φ1+q2φ2+q3φ3]=> φ1=q2/4π ε0r12+q3/4π ε0r13. Увеличивая количество полученных зарядов, можно подсчитать энергию системы , прибавляя новые величины => ∑qnφn/2, где φ2-потенциал той точки поля, в которой находится заряд qn, а поле создается всеми n зарядами. Энергия заряженного конденсатора сосредоточена в поле конденсатора. ∆A=∆qU; C=∆q/U,∆q=CU => ∆H=C∆UU, A=∆Wp=∫dA=∫(0,U)CUdU=CU2/2. Wp= CU2/2=q2/2C=qU/2 – потенциальная энергия заряженного конденсатора. ω=W/V=εε0E2/2 – объемная плотность энергии , зависит от материала диэлектрика и напряженности электрического поля в диэлектрике. Wp= CU2/2=q2/2C=qφ/2 – потенциальная энергия заряженного проводника.
|

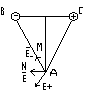 Рассмотрим
треугольник АВС и треугольник AMN, они
подобны.
Е-/E+=((r2+l2/4)1/2/l)E+=E-l/(r2+l2/4)1/2=ql/4πε0(r2+l2/4)
(r2+l2/4)1/2, т.к r>>l EA=ql1/4πε0r3=P/4πε0r3-
напряженность поля на перпендикуляре,
восстановленном из сесредины диполя.
Рассмотрим
треугольник АВС и треугольник AMN, они
подобны.
Е-/E+=((r2+l2/4)1/2/l)E+=E-l/(r2+l2/4)1/2=ql/4πε0(r2+l2/4)
(r2+l2/4)1/2, т.к r>>l EA=ql1/4πε0r3=P/4πε0r3-
напряженность поля на перпендикуляре,
восстановленном из сесредины диполя.
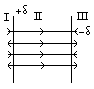 Из принципа
суперпозиции EI=EIII=0. EII=E++[E-]=2δ/2ε0= δ/ε0=>
Напряженность поля бесконечной
плоскости конденсатора не зависит от
расстояния между пластинами,
электрическое поле однородно и
сосредоточено между пластинами.
Из принципа
суперпозиции EI=EIII=0. EII=E++[E-]=2δ/2ε0= δ/ε0=>
Напряженность поля бесконечной
плоскости конденсатора не зависит от
расстояния между пластинами,
электрическое поле однородно и
сосредоточено между пластинами.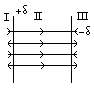 Из принципа
суперпозиции EI=EIII=0. EII=E++[E-]=2δ/2ε0= δ/ε0=>
Напряженность поля бесконечной
плоскости конденсатора не зависит от
расстояния между пластинами,
электрическое поле однородно и
сосредоточено между пластинами.
Из принципа
суперпозиции EI=EIII=0. EII=E++[E-]=2δ/2ε0= δ/ε0=>
Напряженность поля бесконечной
плоскости конденсатора не зависит от
расстояния между пластинами,
электрическое поле однородно и
сосредоточено между пластинами.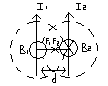 A=ℓIBsina,
по закону Ампера на 1 проводник действует
сила F1=I1B1ℓ1 (sina=1), направление которой
определяется по правилу левой руки.
На второй проводник действует сила
F2=I2B2ℓ2 => два параллельных проводника
по которым текут токи одного напряжения
, притягиваются. Магнитная индукция
прямого тока B=μ0I/2πd, то (ℓ1=ℓ2).
F1=I1μ0I2ℓ/2πd F2=I1μ0I2ℓ/2πd => F1=F2
F=I1μ0I2ℓ/2πd - сила магнитного взаимодействия
токов. F=I1μ0I2/2πd- сила магнитного
взаимодействия, приходящаяся на
единицу длины.
A=ℓIBsina,
по закону Ампера на 1 проводник действует
сила F1=I1B1ℓ1 (sina=1), направление которой
определяется по правилу левой руки.
На второй проводник действует сила
F2=I2B2ℓ2 => два параллельных проводника
по которым текут токи одного напряжения
, притягиваются. Магнитная индукция
прямого тока B=μ0I/2πd, то (ℓ1=ℓ2).
F1=I1μ0I2ℓ/2πd F2=I1μ0I2ℓ/2πd => F1=F2
F=I1μ0I2ℓ/2πd - сила магнитного взаимодействия
токов. F=I1μ0I2/2πd- сила магнитного
взаимодействия, приходящаяся на
единицу длины.
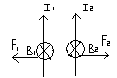 аналогично,
сила взаимодействия определяется
также соотношением F2=I1μ0I2ℓ/2πd. Сила
тока – величина заряда, прошедшего
через поперечное сечение проводника
в единицу времени I=dq/dt. Единицей
измерения силы тока является 1 ампер
(А), устанавливаемый по магнитному
взаимодействию тока. За единицу силы
тока принимают силу тока, при которой
отрезки 2-х параллельных проводников
длиной 1 метр каждый взаимодействует
с силой 2*10-7 Н
аналогично,
сила взаимодействия определяется
также соотношением F2=I1μ0I2ℓ/2πd. Сила
тока – величина заряда, прошедшего
через поперечное сечение проводника
в единицу времени I=dq/dt. Единицей
измерения силы тока является 1 ампер
(А), устанавливаемый по магнитному
взаимодействию тока. За единицу силы
тока принимают силу тока, при которой
отрезки 2-х параллельных проводников
длиной 1 метр каждый взаимодействует
с силой 2*10-7 Н Рассмотрим
схему. В момент переключения ключа
начинается перезарядка, лампа загорится.
Если переключение делать с частотой
50 Гц. по 100 раз в секунду лампа будет
вспыхивать и гаснуть. Если есть
изменения эл. п., то оно замыкает цепь,
дается возможность току вызывать
горение лампы. Изменяющееся во времени
поле между обкладками конденсатора
называется током смещения. Единственным
свойством, объединяющим его с током
проводимости является вызывание им
м. п. D=εε0S. При зарядке конденсатора
вектор D растет, т.е. ∂D/∂t>0 по
направлению с D. При разрядке ∂D/∂t<0
и ∂D/∂t противоположен направлению
D. Переменное эл. поле замыкает ток
проводимости в проводящих проводниках
вызывает включение лампы. I=Iпр+Iси.
Рассмотрим
схему. В момент переключения ключа
начинается перезарядка, лампа загорится.
Если переключение делать с частотой
50 Гц. по 100 раз в секунду лампа будет
вспыхивать и гаснуть. Если есть
изменения эл. п., то оно замыкает цепь,
дается возможность току вызывать
горение лампы. Изменяющееся во времени
поле между обкладками конденсатора
называется током смещения. Единственным
свойством, объединяющим его с током
проводимости является вызывание им
м. п. D=εε0S. При зарядке конденсатора
вектор D растет, т.е. ∂D/∂t>0 по
направлению с D. При разрядке ∂D/∂t<0
и ∂D/∂t противоположен направлению
D. Переменное эл. поле замыкает ток
проводимости в проводящих проводниках
вызывает включение лампы. I=Iпр+Iси.