
- •2) Законы Ньютона. Теорема о движении центра инерции.
- •3) Энергетические характеристики. Потенциальное поле сил. Консервативные и неконсервативные силы.
- •4) Законы сохранения энергии, импульса, и момента импульса механических систем.
- •5) Колебательное движение. Основные понятия: гармонические колебания, осциллятор, амплитуда, частота, период, фаза колебания.
- •6) Уравнение гармонических колебаний в дифференциальной форме.
- •7) Законы изменения величин, характеризующих гармонические колебания.
- •8) Сложение колебаний одинаковой направленности и одинаковой частоты. Векторная диаграмма.
- •9) Биения.
- •10) Сложение взаимно перпендикулярных колебаний.
- •11) Затухающие колебания. Уравнения затухающих колебаний в дифференциальной и интегральной форме, логарифмический декремент затухания.
- •12) Вынужденные колебания. Резонанс.
- •13) Волны. Основные понятия: продольные и поперечные, бегущие и стоячие волны, фронт волны, волновая поверхность, фазовая и групповая скорость.
- •14) Уравнение плоской бегущей волны. Графики, характеризующие смещение точек, участвующих в колебательном процессе, от координаты, от времени.
- •15) Энергия упругой волны. Вектор Умова - Пойтинга.
- •16) Сложение волн. Принцип суперпозиции. Условие образования максимумов и минимумов при интерференции.
- •17) Стоячие волны. Замечание о стоячих волнах в замкнутом пространстве.
- •18) Основные понятия термодинамики: система, параметры состояния, состояние, процесс, графическое изображение процессов, внутренняя энергия, идеальный газ, уравнение состояния, теплоемкость.
- •19) Первое начало термодинамики. С вязь между удельными и молярными теплоемкостями.
- •20) Работа расширения идеального газа в изопроцессах.
- •21) Адиабатический процесс. Уравнение Пуассона.
- •22)Классическая теория теплоемкости идеального газа.
- •23)Основные положения молекулярно - кинетической теории газов и её особенности.
- •24) Основное уравнение молекулярно - кинетической теории газов.
- •25)Распределение молекул идеального газа по скоростям. Наивероятнейшая, средняя квадратичная и средняя арифметическая скорости.
- •26) Среднее число столкновений и средняя длина свободного пробега молекул газа.
- •27) Распределение молекул газа во внешнем поле сил тяготения. Барометрическая формула Лапласа.
- •28) Распределение Больцмана.
- •29) Явление переноса. Диффузия, теплопроводность, внутреннее трение.
23)Основные положения молекулярно - кинетической теории газов и её особенности.
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИЕЙ называется учение, которое объясняет строение и свойства тел движением и взаимодействием атомов, молекул и ионов, из которых состоят тела. В основе МКТ строения вещества лежат три положения, каждое из которых доказано с помощью наблюдений и опытов (броуновское движение, диффузия и др.): 1. вещество состоит из частиц; 2. частицы хаотически движутся; 3. частицы взаимодействуют друг с другом. .Первое положение подтверждают испарение жидкостей и твердых тел
Второе положение МКТ о непрерывном движении частиц подтверждают такие явления, как броуновское движение и диффузия.
Подтверждением третьего положения МКТ о взаимодействии частиц является возникновение упругих сил при деформациях тел, существование различных агрегатных состояний (твердого, жидкого, газообразного) одного и того же вещества.
![]()
![]()
![]() .
.
 .
.

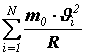 .
.
 .
.
 ,
,
где
 –
объём сосуда с газом.
–
объём сосуда с газом.

 или
или
![]() (9)
(9)
 .
(10)
.
(10)
![]() ,
(11)
где n
,
(11)
где n
![]() –концентрация
молекул.
–концентрация
молекул.
Это уравнение называется основным уравнением молекулярно-кинетической теории идеального газа.
Получим связь давления со средней кинетической энергией поступательного движения молекулы
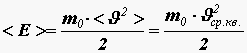 .
(12)
.
(12)
Из
формулы (11)
 ,
следовательно:
,
следовательно:
![]() .
(13)
.
(13)
24) Основное уравнение молекулярно - кинетической теории газов.

![]() ,
,
где
z
– число столкновений всех молекул со
стенкой, которое пропорционально
концентрации молекул в газе, скорости
молекул и площади поверхности стенки:
![]() .
.
К
стенке движется только половина молекул,
остальные движутся в обратную сторону:
 .
.
Тогда
полный импульс, переданный стенке за 1
секунду:
 .
.
Согласно
второму закону Ньютона изменение
импульса тела за единицу времени равно
действующей на него силе:
![]() .
.![]() ;
;![]() .
.
Тогда давление газа на стенку сосуда равно:
 -
-
основное уравнение МКТ.
Обозначив
среднее значение кинетической энергии
поступательного движения молекул
идеального газа:
 ,
получим
,
получим
 ,
где
p
- давление газа,
V
- объем, занимаемый данным количеством
молей
газа,
n
- количество молей,
R
- универсальная
газовая постоянная,
T
- абсолютная
температура,
a,
b
- константы Ван-дер-Ваальса, подбираемые
для разных газов эмпирически по величинам
отклонений от идеального поведения.
Они бывают рассчитаны на 1 моль газа, их
численные значения можно найти в
специальных таблицах.
,
где
p
- давление газа,
V
- объем, занимаемый данным количеством
молей
газа,
n
- количество молей,
R
- универсальная
газовая постоянная,
T
- абсолютная
температура,
a,
b
- константы Ван-дер-Ваальса, подбираемые
для разных газов эмпирически по величинам
отклонений от идеального поведения.
Они бывают рассчитаны на 1 моль газа, их
численные значения можно найти в
специальных таблицах.
На диаграмме (V,P) описанный процесс изображается изотермой,
|
|
Уравнение Ван-дер-Ваальса
|
|
|
где
a
и b
- константы, зависящие от свойств
вещества. При a = b = 0
уравнение (1)
превращается в уравнение состояния
идеального газа
![]()
25)Распределение молекул идеального газа по скоростям. Наивероятнейшая, средняя квадратичная и средняя арифметическая скорости.

26) Среднее число столкновений и средняя длина свободного пробега молекул газа.
Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна:
|
|
|
|
|
где
![]() –
средняя скорость теплового движения,
τ – среднее время между двумя
столкновениями. Именно
–
средняя скорость теплового движения,
τ – среднее время между двумя
столкновениями. Именно![]() -
средняя длина свободного пробега нас
интересует (рис. 3.1).
-
средняя длина свободного пробега нас
интересует (рис. 3.1).
За одну секунду молекула проходит путь,
равный средней арифметической скорости
![]() .
За ту же секунду молекула претерпевает
ν столкновений. Следовательно,
.
За ту же секунду молекула претерпевает
ν столкновений. Следовательно,
|
|
|
Подсчитаем число столкновений ν.
Вероятность столкновения трех и более молекул бесконечно мала.
Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 3.3).
Путь,
который пройдет молекула за одну секунду,
равен длине цилиндра
![]() .
Умножим объём цилиндра
.
Умножим объём цилиндра![]() на
число молекул в единице объёмаn,
получим среднее число столкновений в
одну секунду:
на
число молекул в единице объёмаn,
получим среднее число столкновений в
одну секунду:
|
|
|
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга.
По закону сложения случайных величин
|
|
|
А
так как средняя длина свободного пробега
![]() то
получим:
то
получим:
|
|
|
|
Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т.
Так
как
![]() ,
то есть
,
то есть![]() то
то
|
|
|
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:
|
|
|
