Выводы по главе 1
В данной главе разобрано несколько примеров потери местной или общей устойчивости, приведших к обрушения пролетного строения.
Следует отметить, что потеря местной устойчивости, зачастую ведет не к разрушению пролетного строения, а к затруднениям при его эксплуатации и требует разработки дополнительных мер.
В данной главе даны общие понятия о потери устойчивости и разобраны основные факторы влияющие на устойчивость конструкции или элемента
Глава 2. Обзор методик оп расчету устойчивости
Исходя из приведенных ранее данных ясно, что надежность конструкции не может зависеть только от прочности. Даже если конструкция прочная, увеличение нагрузки или случайное воздействие могут привести к потере устойчивости конструкции и ее разрушению или непригодности для использования. Возьмем, к примеру, самый простой элемент, прямой длинный стержень, который может внезапно согнуться под действием продольной сжимающей силы и потерять свою форму. Если стержень не обладает достаточной прочностью, внутренние силы в конечном итоге заставят его сломаться.
Потеря устойчивости может происходить в стержневых системах, пластинах и оболочках. Устойчивость конструкций, простых или сложных, зависит от устойчивости отдельных элементов и их совместной работы. Очень важно знать, стабильна структура или нет, потому что незначительные причины могут заставить ее потерять устойчивость и привести к быстрым изменениям или разрушению. Многие сооружения, такие как мосты и высотные здания, были разрушены из-за потери устойчивости. В строительной механике есть специальный раздел, посвященный вопросам расчета устойчивости, включающий теоретические принципы, методы и прикладные задачи определения критических нагрузок и форм потери устойчивости, а также влияния случайных напряжений на поведение конструкции.
В данной главе будут подробно рассмотрены основные методы и подходы к оценке устойчивости.
2.1. Статистический метод или метод Эйлера
Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Решение Эйлера считается классическим решением, и, хотя оно сформулировано только для сжатых стержней, для своего времени оно было прорывным. Далее на его основе были разработаны варианты решения для более сложных элементов и форм нагружения.
Формулируется решенная Эйлером задача следующим образом:
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Рассматриваемый метод решения основан на том, что при достижении силой F критического состояния (F=Fкр) стержень находится в безразличном состоянии и ему присущи две формы равновесия: прямолинейная и криволинейная (в таких случаях говорят, что происходит ветвление, или бифуркация, равновесных состояний). Для выявления криволинейной формы равновесия достаточно приложить к стержню малую поперечную возмущающую нагрузку Q, которая вызовет малый прогиб. Если F<Fкр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы.
Применительно к строительным конструкциям долгое время считалось, что решения Эйлера достаточно, т.к. до определенного момента потеря устойчивости в строительных конструкциях была присуща только стержневым элементам. В первую очередь это были различные стойки опор или сжатые пояса ферм.
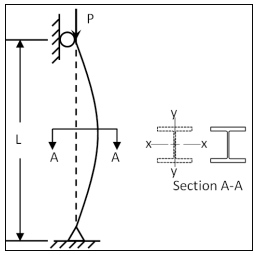
Рисунок 2.1 - Изгибная деформация колонны с широким фланцем
Режим изгиба, который обычно рассматривается во всех курсах по проектированию конструкционных сталей, — это режим изгиба при изгибе. В результате большинство инженеров лучше всего знакомы с деформацией при изгибе, которая включает в себя поперечный сдвиг поперечного сечения вокруг одной из основных осей, как показано на рисунке 2.1. Колонну со штыревым концом на рис. 2.19 часто называют колонной Эйлера в честь Леонарда Эйлера, который был первым человеком, разработавшим в середине 1700-х годов математическую формулировку для прогнозирования способности колонн с осевой нагрузкой к упругому изгибу.
Упругое решение, разработанное Эйлером для столбика со штыревым концом, приведено в следующем выражении:
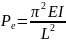(2.1)
Где:
PE = критическая упругая нагрузка на изгиб (нагрузка Эйлера)
E = модуль упругости
I = момент инерции секции относительно оси изгиба (y-ось y на рисунке)
L = длина столбца без скобок
Управляющая способность колонны к изгибу, показанная на рис. 2.1, должна быть наименьшей из величин изгиба относительно осей x-x и y-y. Если длина без скобок одинакова для двух оси, меньший момент инерции будет определять способность к изгибу. По этой причине ось y-y часто называют слабой осью, поскольку Iy<Ix в I-образных элементах, обычно их называют двутавровыми балками. Однако прочная ось все еще может контролировать изгиб, если длина без скобок больше относительно этой оси или если условия поступательной или вращательной поддержки различны относительно двух осей.
Уравнение 2.1 применимо к столбцам с закрепленными концами. Для более общих задач часто используется эффективный коэффициент длины (K), что приводит к следующему выражению:
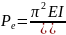(2.2)
Коэффициент эффективной длины преобразует колонну в конструктивной системе в эквивалентную Колонна Эйлера. Физическое представление эффективного коэффициента длины изображено на Рисунок 2.2. Колонны в раме портала закреплены у основания и удерживаются балкой вверху. Эффективный коэффициент длины колонны в конструктивной системе зависит от относительной жесткости между колоннами и удерживающей балкой в верхней части рамы. Коэффициент эффективной длины преобразует столбцы во фрейме в эквивалентная длина столбца Эйлера с заостренным концом на рисунке.
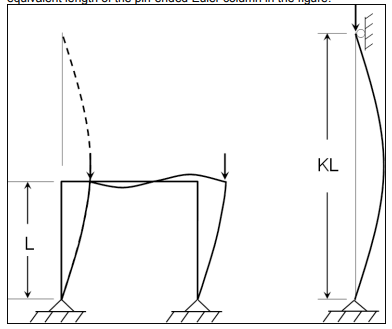
Рисунок 2.2 - Эффективный коэффициент длины
Эффективные коэффициенты длины при изгибе часто делятся на две категории в зависимости от состояния крепления колонны. Столбцы на рис. 2.2 являются частью несъемная рама, которая может раскачиваться из стороны в сторону. Диапазон эффективных коэффициентов длины для несъемных рам составляет 1,0 ≤ Ksway < ∞. Для элементов со скобами, концы которых не могут смещаться относительно друг друга, диапазон эффективных коэффициентов длины составляет 0,5 ≤ Knosway ≤ 1,0. Во многих спецификациях или связанных с ними разделах комментариев приводится цифра, аналогичная показанной на рис. 2.3, которая сводит в таблицу K-коэффициенты для идеализированных условий поддержки. Такая цифра полезна для указания диапазона K-коэффициентов для идеализированных колонн; однако большинство конструкций не соответствуют идеализированным условиям опоры. Поэтому при проектировании обычно желательно решение, которое может учитывать изменяющиеся условия опоры. Доступно более общее решение с выравниванием диаграмма, которая обычно приводится в большинстве спецификаций на проектирование.
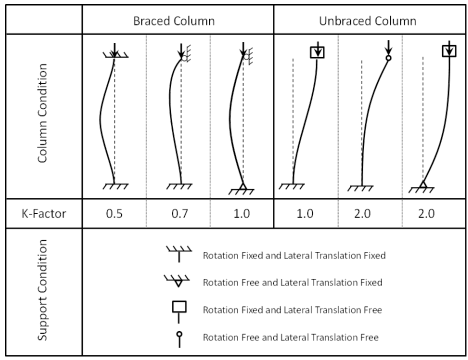
Рисунок 2.3 - K коэффициентов для идеализированных условий поддержки
Как отмечалось ранее, технические характеристики конструкции обычно предусматривают как эластичные, так и неэластичные решения для предотвращения потери устойчивости. Поскольку решения, как правило, зависят от предела текучести материала, решения по изгибу иногда предоставляются в терминах напряжения, а не силы. Деление обеих частей уравнения 2.2 на площадь поперечного сечения приводит к напряжению и дает следующую формулировку:
(2.3)
Где:
Pn = номинальная прочность на изгиб)
PE = нагрузка Эйлера на изгиб
Po = предел текучести сечения
Fy = номинальный предел текучести материала колонны
Ag = общая площадь колонки
Например, согласно AASHTO также включает добротность при расчете Po, которая является фактором, учитывающим тонкие элементы поперечного сечения, на которые может повлиять локальная деформация. Изгибная деформация - это режим изгиба, который может управлять конструкцией любого двусимметричные или односимметричные сечения. Термин "двусимметричный" относится кучастку с двумя осями симметрии, в то время как односимметричный участок обладает единственной осью симметрии. Некоторые типичные двусимметричные и односимметричные сечения изображены на рис. 2.4.
Изгиб при кручении
Другим потенциальным режимом, который следует учитывать для колонн с осевой нагрузкой, является изгиб при кручении, при котором нестабильность связана с чистым перекручиванием сечения. Точка, вокруг которой изгибается секция, зависит от свойств поперечного сечения и крепления детали, которые используются. Предполагаемым центром закручивания для большинства колонн является центр среза секции; однако, как будет рассмотрено далее в этом разделе, в зависимости от деталей боковых креплений некоторые колонны могут закручиваться вокруг ограниченной оси. Прежде чем обсуждать поведение при изгибе, целесообразно провести краткий обзор свойств секции при кручении. Сопротивление кручению в тонкостенных элементах обусловлено либо жесткостью на кручение по Сен-Венану, либо жесткостью на деформацию при кручении. Жесткость Сен-Венана часто называется равномерным кручением, поскольку жесткость не изменяется по длине и также не чувствительна к условиям опоры секции. Кручение по методу Сен-Венана приводит к чистой деформации сдвига в плоскости пластин, составляющих элемент.
Рисунок 2.4 - Типичные двух- и односимметричные сечения
Сопротивление деформации при кручении, с другой стороны, часто называют неравномерным кручением, поскольку жесткость связана с деформацией при изгибе в плоскости отдельных пластин, составляющих секцию. Деформирующая жесткость секции связана к стойкости элемента к деформациям при короблении.
Две двутавровые балки, подвергающиеся воздействию крутящего момента на концах, показаны на рисунке 4-8, чтобы проиллюстрировать деформацию при перекосе, а также жесткость при перекосе. Приложенный крутящий момент указывается с использованием правила правой руки (направьте большой палец правой руки в направлении двойной стрелки, а пальцы согните в направлении приложенного крутящего момента). На рис. 2.5 показано, что деформация короблением заключается в скручивании фланцев относительно друг друга вокруг вертикальной оси через полотно. Деформирующая деформация искажает поперечное сечение таким образом, что оно больше не является плоским сечением, поскольку два фланца искривились относительно друг друга. Скручивание вокруг продольной оси элемента на рис. 2.5 а предотвращается с одного конца; однако деформирующие деформации не ограничиваются. Поскольку секция может деформироваться по всей длине, фланцы остаются прямыми при скручивании относительно друг друга, и элемент обладает только жесткостью на кручение по Сен-Венану.
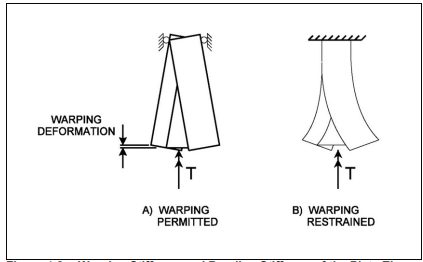
Рисунок 2.5 - Жесткость на деформацию и изгиб пластинчатых элементов
Широкий участок фланца на рис. 2.5 б подвержен как скручиванию, так и деформированию при перекручивании предотвращен с одного конца. При ограничении деформации только в одном месте по длине элемент не может скручиваться без сгибания фланцев. Поскольку фланцы должны изгибаться при скручивании элемента, следовательно, секция обладает жесткостью при деформации. Деформирующее кручение создает продольные напряжения во фланцах элемента.
Многие элементы не имеют физических удерживающих устройств, предотвращающих деформацию, как показано на рисунке 4-8B; однако элемент по-прежнему обладает деформирующей жесткостью, если предотвращено скручивание как минимум в двух точках вдоль продольной оси. Концевые условия ограничения скручивания препятствуют предотвращают вращение секции вокруг продольной оси, но в остальном специально не ограничивают деформацию секции при перекосе. Поскольку жесткость при изгибе очень чувствительна к длине без опоры, жесткость при деформировании сильно зависит от величины длины без опоры. Большая длина изгиба пластинчатых элементов при скручивании элемента приводит к снижению сопротивления деформации при кручении по сравнению с меньшей длиной изгиба.
2.2. Динамический метод
Динамический метод, также известный как метод малых колебаний, заключается в изучении колебаний системы при отклонении ее от нормального состояния. Даже если на систему не действуют внешние силы, в данном методе их все равно необходимо рассматривать как динамические силы. Динамическая система может вести себя по-разному. В случае устойчивой системы, испытывающей небольшие отклонения, она будет производить гармонические колебания с определенной частотой и ограниченной амплитудой. Напротив, индифферентная система останется в том же положении без каких-либо колебаний, а неустойчивая система продолжит свое движение как апериодическая система. Частота апериодического движения является отрицательной величиной по динамике.
Итак, в устойчивой системе частота собственных колебаний ω>0, в безразличной системе ω=0, в неустойчивой системе ω2<0.
Динамический метод применяется с целью определения максимально допустимой нагрузки, ограниченной пластическими деформациями элементов рам или их соединений [1,2], и критическую нагрузку, ограниченную устойчивостью рам [3,4]. Мотивация к определению точного значения критической силы обусловлена ее использованием следующим образом :
- критическая нагрузка - это максимально допустимая нагрузка для данной конфигурации каркаса и может использоваться в качестве критерия совершенства или эффективности конструкции;
- используется в расчетах, предписанных стандартами для проектирования элементов конструкций при совместном воздействии сжатия и изгиба [5];
- используется для проверки теоретического анализа устойчивости при различных конечных состояниях колонн каркасов [6].
В динамическом методе неразрушающего контроля рам на критическую нагрузку [7,8,9] используется зависимость нестабильности от жесткости конструкции. Многие теоретические и экспериментальные исследования подтверждают уменьшение частоты свободных колебаний с увеличением усилий сжатия [10]. Критическая нагрузка, определенная на основе результатов измерения частоты для различных нагрузок путем экстраполяции до нулевой частоты в соответствии к линейной зависимости квадрата частоты от нагрузки сжатия. При испытании рам в режиме качания вертикальная нагрузка выполняется с использованием дополнительных грузов [9,11], непосредственно с помощью рычажной системы [12] или с помощью специального механизма (имитатор гравитационной нагрузки) [13].
В настоящей работе предложен новый неразрушающий метод определения критической нагрузки на изгиб шпангоутов в режиме бокового раскачивания. Способ позволяет проводить измерения во время испытаний при нагрузках, превышающих критические нагрузки на раму, без потери ее устойчивости. Технологический преимуществом этого метода является возможность создавать нагрузки, соответствующие критическим нагрузкам реальных полноразмерных кадров.
Повышение точности достигается за счет проведения экспериментов в диапазоне вертикальных нагрузок, включая критическую нагрузку, а также за счет использования системы нагружения без трения.
Поскольку боковые колебания рамы вызывают вертикальные перемещения балки, поддержание стабильного натяжения достигается с помощью гидравлического или пневматического нагружающего устройства или путем включения дополнительного пружинящего элемента в случае механического нагружающего устройства (D).
Эксперимент заключается в определении естественного частота колебаний системы при различных значениях силы натяжения в тяговом элементе и, соответственно, сил сжатия в колоннах рамы. Принимая боковое перемещение каркасной балки за степень свободы, обобщенная масса M' системы может быть представлено в следующем виде:
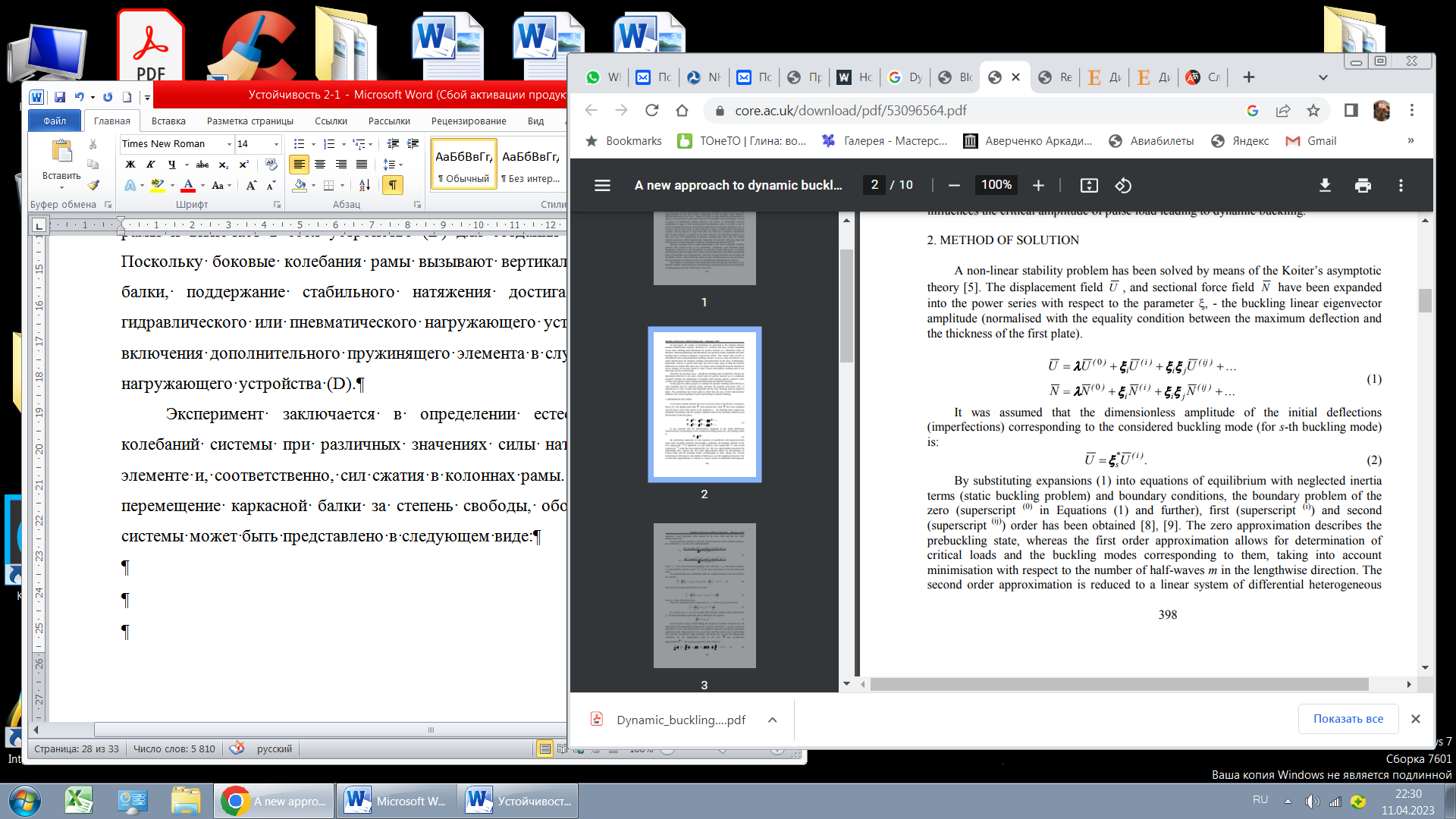
Предполагалось, что безразмерная амплитуда начальных прогибов (дефектов), соответствующая рассматриваемому режиму потери устойчивости (для s-го режима потери устойчивости) является:
Путем подстановки разложений (1) в уравнения равновесия с пренебрежением членами инерции (задача о статическом изгибе) и граничными условиями краевая задача нулевого (верхний индекс (0) в уравнениях (1) и далее), первого (верхний индекс (i)) и второго (верхний индекс (ij)) порядка имеет были получены [8], [9]. Нулевое приближение описывает состояние предварительной деформации, тогда как приближение первого порядка позволяет определить критические нагрузки и соответствующие им режимы деформации с учетом минимизации количества полуволн m в продольном направлении. Приближение второго порядка сводится к линейной системе дифференциально-неоднородных уравнений, правые части которых зависят только от силового поля и перемещений первого порядка.
Найдя решения краевой задачи первого и второго порядка, были определены коэффициенты aijs, bijks [8]:
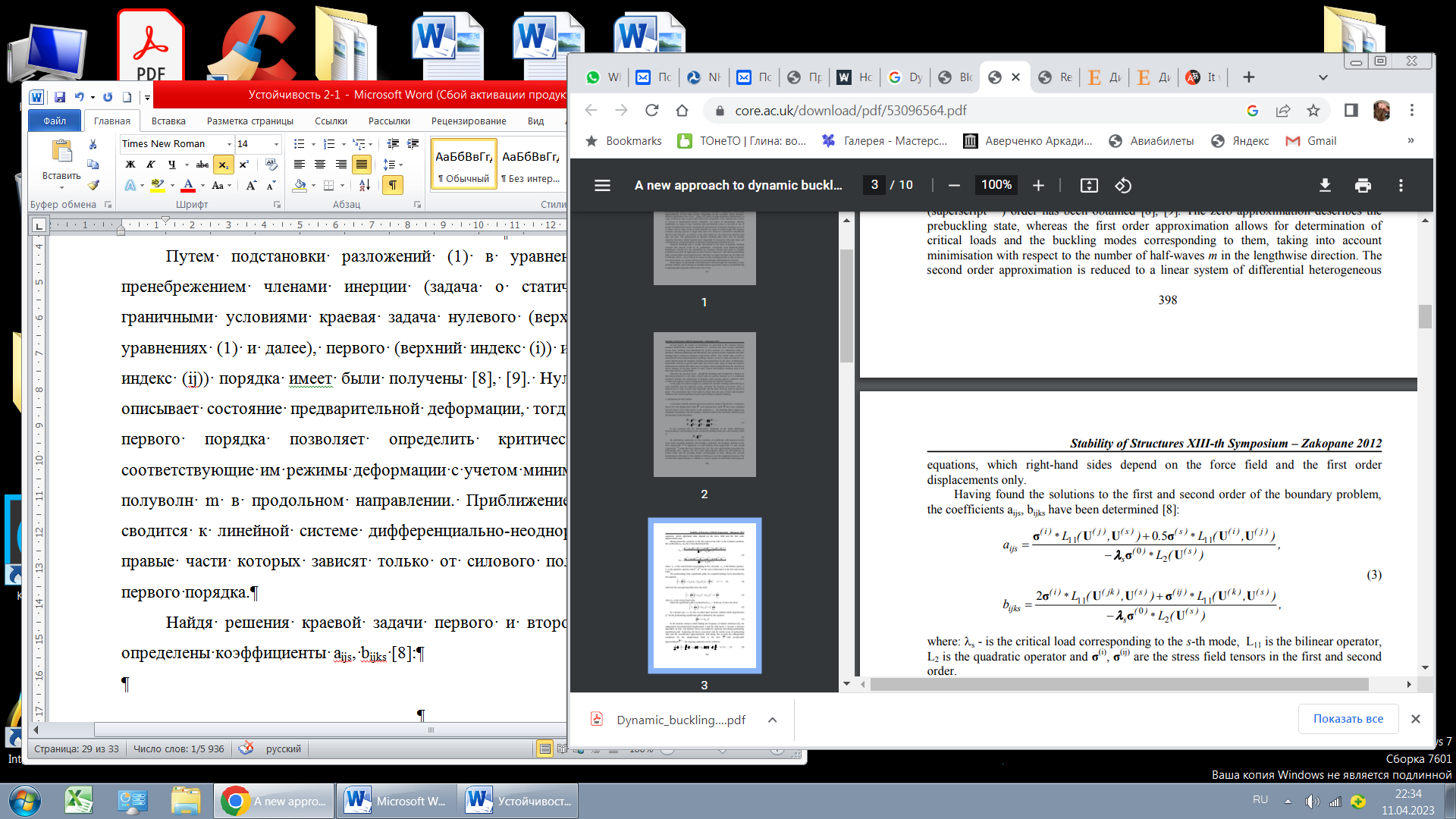
где: λs - критическая нагрузка, соответствующая s-му режиму, L11 - билинейный оператор, L2 - квадратичный оператор, а σ(i), σ(ij) - тензоры поля напряжений первого и второго порядка.
Траектории статического равновесия после изгиба при сопряженном изгибе могут быть описаны уравнением:
которые для несвязанной задачи имеют вид:
где λcr - значение критической нагрузки.
Когда траектория равновесия симметрична (a111 = 0), уравнение. (5) иметь вид:
В частном случае, т.е. для так называемой идеальной структуры без начальных несовершенств (ζ*=0) траектория равновесия после выброса определяется уравнением:
При динамическом анализе (при нахождении частоты собственных колебаний [9]) независимое безразмерное смещение ζ и коэффициент нагрузки λ становятся функцией зависящий от времени, и динамические члены были добавлены к уравнениям, описывающим траекторию равновесия после выброса. Пренебрегая силами, связанными с условиями инерции состояния предварительного сжатия, и приближениями второго порядка, и принимая во внимание условия ортогональности для поля смещения в первом U(i ) и приближение второго порядка U(ij ), уравнения Лагранжа можно записать в виде:
где ὠs - собственная частота с режимом, соответствующим режиму деформации; aijs и biijks - коэффициенты, описывающие поведение конструкции после деформации (независимо от времени); однако параметры нагрузки λ и смещения ζ являются функциями времени до.
Для несвязанного изгиба, т.е. одномодового изгиба (где индекс s = N = 1), уравнения движения могут быть записаны в виде:
Предполагается, что в начальный момент времени t = 0 безразмерное перемещение ζ, а также скорость перемещения равны нулю, т.е.:
Результаты расчетов, представленные в этой главе, позволяют обсудить эффект от применения следующих критериев:
простейший критерий, предложенный Вольмиром [13] - динамическая критическая нагрузка соответствует амплитуде импульсной силы (постоянной длительности), при которой максимальный прогиб пластины равен некоторому постоянному значению k (k= половина или одна толщина пластины).
Критерий устойчивости Budiansky&Hutchinson [3], который гласит: потеря динамической устойчивости происходит, когда максимальный прогиб пластины быстро растет при небольшом изменении амплитуды нагрузки.
Рассматривается квадратная композитная плита с простой опорой, отношение длины к толщине которой равно 100. Пластина подвергается однонаправленному сжатию в виде прямоугольной импульсной нагрузки P конечной длительности. Незагруженные края пластины остаются прямыми и параллельными во время загрузки.
Для численного расчета была принята ортотропная модель. Необходимые значения модулей Юнга и коэффициентов Яда были рассчитаны с использованием уравнений, основанных на теории смесей [4], которые являются следующими:
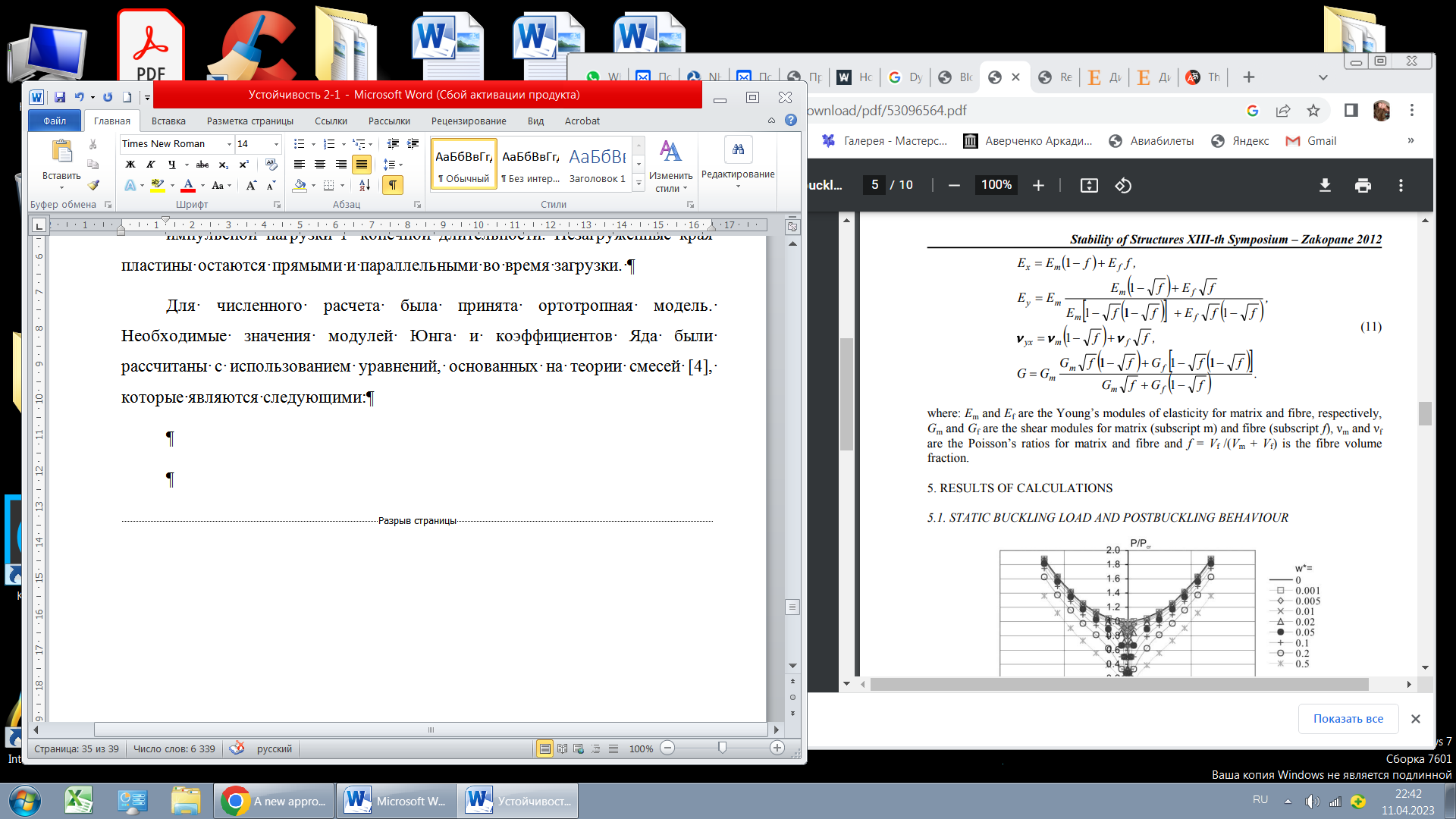
где: Em и Ef - модули упругости Юнга для матрицы и волокна соответственно, Gm и Gf - модули сдвига для матрицы (индекс m) и волокна (индекс f), vm и vf - коэффициенты Пуассона для матрицы и волокна, а f = Vf /(Vm + Vf) – объемная доля волокна.
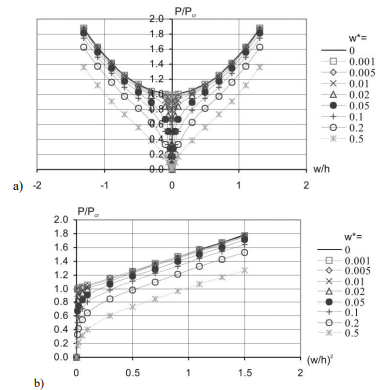
Рисунок 2.7 - Безразмерная нагрузка P/Pcr в зависимости от безразмерного отклонения (a) или квадрата безразмерного отклонения (b)
Для идеальной пластинчатой конструкции критическая нагрузка может быть определена на основе анализа собственных значений, но для конструкций с несовершенством нагрузка на изгиб может быть определена на основе поведения до и после изгиба. Авторы решили использовать два хорошо известных метода определения критической нагрузки, которые обычно применяются к результатам экспериментальных исследований.
Метод точки перегиба (P-w), который очень похож на метод “верхней части колена” и альтернативу (P-w2) был использован метод [9]. Траектории равновесия после изгиба для пластин с начальными дефектами, соответствующими режиму изгиба, и различными амплитудами w*=w0 /h (где: w0 - амплитуда дефекта, h - толщина пластины) представлены на рис. 2.7. С использованием упомянутых выше методов была найдена нагрузка на изгиб Pcr*/Pcr для пластины с геометрическими дефектами, которая представлена в таблице 2 (где Pcr* - изгиб при сжатии усилие для несовершенной пластины и Pcr - бифуркационная нагрузка).
Таблица 2.1. Pcr*/Pcr для различной амплитуды начального несовершенства
Метод определения: начальная амплитуда несовершен w* |
P-w Pcr*/Pcr |
P-w2 Pcr*/Pcr |
0,001 0.005 0.01 0.02 0.05 0.1 0.2 0.5 |
0.999 0.998 0.995 0.990 0.968 0.925 0.834 0.589 |
0.999 0.994 0.986 0.968 0.925 0.863 0.751 0.494 |
Из таблицы 2.1 следует, что более низкие значения Pcr* были получены с использованием P-w2, метод и различия между результатами обоих методов возрастают с увеличением значения амплитуды несовершенства.
В дальнейших исследованиях были приняты во внимание значения Pcr*, полученные на основе метода точек перегиба (P-w метод).
В большинстве публикаций, посвященных проблеме динамического изгиба, амплитуда начального несовершенства принималась равной w* = 0,01, при котором снижение нагрузки на изгиб очень мало, примерно на 1%.
Коэффициент динамической нагрузки DLF определяется как отношение амплитуды импульсной нагрузки к критической статической нагрузке на изгиб для идеальных конструкций. Представленные ниже расчеты были сделано с целью проверить, как способ оценки DLF влияет на критическую амплитуду импульсной нагрузки, приводящей к динамическому изгибу. Авторы предлагают ввести динамический коэффициент нагрузки DLF* =Р/Рср* - амплитуда импульсной нагрузки, деленная на статическую нагрузку на изгиб для несовершенных конструкций.
Расчеты проводились для двух значений длительности импульса T0=T и T0=0,5T (где T - период естественной изгибной вибрации основания пластины, для предполагаемых свойств материала и геометрии T=0,59 мс).
В таблицах 2.2 и 2.3 приведены коэффициенты критической динамической нагрузки DLFcr (определяемые обычным способом) и DLF*cr (определяется по DLF* представлены соотношения (вт/ч), где амплитуда импульсной нагрузки делится на деформирующую нагрузку для несовершенных конструкций). Критическое значение коэффициента динамической нагрузки DLF*cr рассчитывали как амплитуду импульсной нагрузки, деленную на статическую нагрузку на изгиб для конструкции с начальным несовершенством с использованием метода точек перегиба (см. таблицу 2.2, столбец P-w).
Таблица 2.2. DLFcr и DLFcr* для разной амплитуды начального несовершенства, T0=T
Предполагаемый критерий: начальная амплитуда несовершенства w* |
Критерий Вольмира (w/t)cr = 1 DLFcr |
Критерий Будианского-Хатчинсона DLFcr |
Критерий Вольмира (вт/т)cr = 1 DLF* |
Критерий Будианского- Хатчинсона DLF*cr
|
0,01 0.02 0.05 0.1 0.2 0.5 |
1.49 1.31 1.17 1.07 1.13 0.63 |
1.4 – 1.6 1.2 – 1.3 0.8 – 0.9 0.8 – 0.9 0.7 – 0.8 0.4 – 0.5 |
1.49 1.32 1.21 1.15 1.10 1.08 |
1.4 – 1.6 1.2 – 1.3 0.9 – 1.1 0.9 – 1.0 0.84 – 0.96 0.7 – 0.85 |
Таблица 2.3. DLFcr и DLFcr* при различной амплитуде начального несовершенства T0=0,5T
Предполагаемый критерий: начальная амплитуда несовершенства w* |
Критерий Вольмира (w/t)cr = 1 DLFcr |
Критерий Будианского-Хатчинсона DLFcr |
Критерий Вольмира (вт/т)cr = 1 DLF* |
Критерий Будианского- Хатчинсона DLF*cr
|
0,01 0.02 0.05 0.1 0.2 0.5 |
3.07 2.47 1.89 1.40 1.01 0.62 |
4.4 – 4.6 3.4 – 3.6 2.0 – 2.8 1.6 – 1.8 1.0 – 1.2 0.4 – 0.6 |
3.08 2.49 1.86 1.51 1.21 1.01 |
4.4 – 4.6 3.4 – 3.6 2.5 – 2.9 1.7 – 1.9 1.2 – 1.4 0.7 – 1.0 |
Значения DLF(вт/ч) и DLF*(вт/ч) для трех значений несовершенства амплитуды и длительности двух импульсов (T0=T и T0=0,5T) представлены на рис. 2.8. На этих рисунках показаны статические кривые P/Pcr (для плоских пластин) и P/Pcr* после вскрытия (для несовершенной пластины) также нарисованы.
Можно заметить, что при относительно небольшой амплитуде несовершенства w*=0,01 (рис. 2.8) кривые DLF(вт/ч) и DLF*(вт/ч) перекрываются при заданной длительности импульса T0. Кроме того, статические кривые после подтягивания перекрываются (исключая начальный диапазон отклонений). В этом случае характер динамических откликов сильно зависит от предполагаемой длительности импульса - для при более коротком импульсе прогибы невелики, а динамическая нагрузка на изгиб по меньшей мере в три раза больше (см. таблицы 2.2 и 2.3).
Когда амплитуда дефектов вырастет до значения w*=0,1 (Рис. 2.9) различия между кривыми DLF и DLF* отчетливо видны как для длительности импульсов, так и для статических кривых после обработки P/Pcr (для плоской пластины) и P/Pcr* также различаются. Результат динамических откликов для длительностей импульсов T0=T и T0=0,5T аналогичен, но динамический нагрузка на изгиб при более коротком импульсе в два раза больше, чем при T0=T.
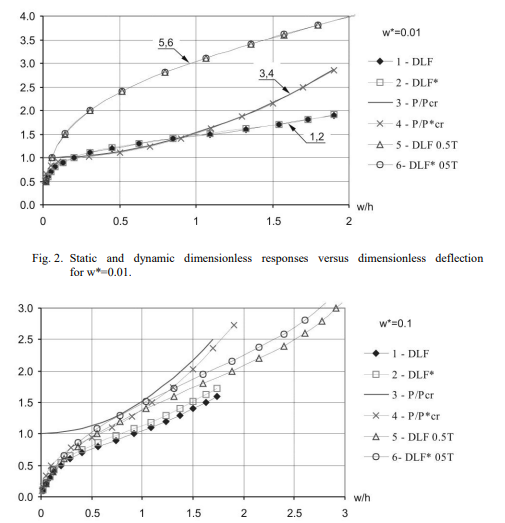
Рисунок 2.8 - Статические и динамические безразмерные характеристики в зависимости от безразмерного отклонения при w*=0,01.
Рисунок 2.9 - Статические и динамические безразмерные характеристики в зависимости от безразмерного отклонения при w*=0,1.
При относительно большом значении w* (амплитуда несовершенства равна половине толщины пластины) - рис. 2.9, результаты показывают, что динамические характеристики пластины не зависят от длительности импульсной нагрузки (соотношения DLF(вт/ч) для T0=T и для T0=0,5T охватывают up, а также DLF*(вт/ч) для обоих предполагаемых перекрывающихся импульсов) и, кроме того, курсы DLF* (w/h) почти идентичны статической кривой после смешивания P/Pcr*
Следует подчеркнуть, что различия между курсами DLF (оцениваемые как соотношение амплитуда импульсной нагрузки к статической бифуркационной нагрузке) и DLF* (оценивается как отношение амплитуды импульсной нагрузки к статической нагрузке на изгиб несовершенной пластины) хорошо видны на рис. 2.9. Статические и динамические безразмерные характеристики в зависимости от безразмерного отклонения при w*=0,5.