3. Графический метод решения игр 2хn и mх2.

Рассмотрим подробно случай 2хn- игр. Пусть игрок А имеет в своем распоряжении две чистых стратегии, а игрок В – n чистых стратегий. Матрица выигрышей игрока А имеет вид:

.

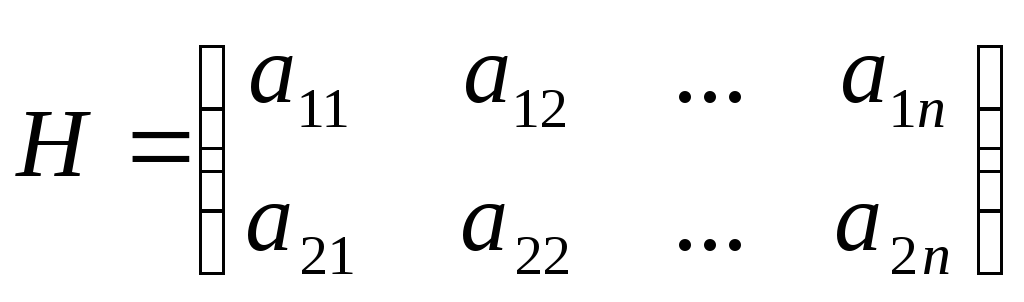Смешанная стратегия игрока А задается вектором S_А=(р₁, р₂), где р₁+р₂=1, р₁0, р₂0. Положим р₁=р, тогда р₂=1р, где р[0, 1]. Поэтому S_А=(р, 1р), т. е. смешанная стратегия игрока А однозначно определяется екоторым числом р[0, 1].

Если игрок В применит свою чистую стратегию В_j (j=1,…,n), то средний выигрыш игрока А в одной партии при использовании стратегии S_A=(p,1p) определяется выражением H(S_A,B_j)=a_1jp+a_2j(1p)=z_j(p) при всех j=1,…,n..

Функции z_j(p) – линейные функции на отрезке р[0,1]. Изобразим их графики на рисунке.

Каждой чистой стратегии В_j игрока В соответствует своя прямая Н=z_j(p). Игрок В стремится к уменьшению своего проигрыша. Следовательно, при фиксированной стратегии S_A=(p,1p) его противника игрок В выбирает ту стратегию В_j, для которой график функции Н=z_j(p) при данном р расположен ниже других.

Таким образом, наименьшим выигрышам игрока А при неблагоприятных для него действиях игрока В соответствует нижняя огибающая всех прямых Н=z_j(p) на рисунке.

С другой стороны, целью игрока А является достижение наибольшего гарантированного выигрыша при любых действиях партнера. Значит, он будет выбирать ту стратегию S_A*=(p*,1p*), которая определяется точкой р*, соответствующей максимуму нижней огибающей. Именно эта стратегия и является оптимальной для игрока А, а само значение максимума огибающей определяет цену игры.

Теперь найдем оптимальную смешанную стратегию игрока В. В зависимости от формы нижней огибающей, может представиться два случая. Рассмотрим каждый из них.

Случай 1. Нижняя огибающая имеет ровно одну максимальную точку (р*, Н*). При этом заметим, что если в исходной матрице отсутствуют доминируемые стратегии, то точка максимума р* является внутренней точкой отрезка [0, 1].

Итак, пусть р*(0, 1). Тогда в пиковой точке нижней огибающей пересекается не менее двух прямых, из которых одна имеет положительный наклон, а другая – отрицательный.

Выделим любую пару таких прямых, например, z=z_k(p) и z=z_l(p), которым соответствуют чистые стратегии В_k и В_l. Нетрудно показать, что для минимизации собственного проигрыша игроку В достаточно использовать только эти стратегии, а от применения других чистых стратегий воздержаться. Тем самым получим вспомогательную игру с платежной матрицей:

(матрица получается изН вычеркиванием всех столбцов, кроме k-го и l-го). Оптимальная стратегия S_B=(q₁, q₂) игрока В и цена игры в получившейся игре 2х2 могут быть найдены с помощью формул (2.7). Тогда оптимальной стратегией игрока В в первоначальной задаче является стратегияS_B*, в которой k-й и l-й компоненты равны соответственно q₁ и q₂, а остальные компоненты равны нулю. Цена вспомогательной игры совпадает с ценойv_S исходной игры. Аналогично могут быть рассмотрены и другие пары прямых, проходящих через пиковую точку и имеющих разнознаковые наклоны.

Замечание. В рассмотренном случае игрок В с точки зрения принципа минимакса может обладать несколькими оптимальными стратегиями. Однако, исследуя ситуацию и с других позиций, среди множества оптимальных стратегий игрока В можно выделить наиболее приемлемую. В данном случае, по-видимому, следует предпочесть ту стратегию игрока В, которая соответствует паре прямых с наибольшими отрицательным и положительным наклонами, т. е. прямыми, имеющими с нижней огибающей общие отрезки.

Случай 2. Нижняя огибающая содержит горизонтальный участок, соответствующий отрезку [p₁*,p₂*] на оси абсцисс.

Тогда любая стратегия видаS_A*=(p, 1p), где р[p₁*,p₂*], является оптимальной для игрока А. Игрок В обладает единственной чистой стратегией, которой соответствует прямая, содержащая данный горизонтальный участок.

Пример 2.6. Решим игру с платежной матрицей:

Сначала упростим матрицу с помощью отбрасывания доминируемых стратегий. Стратегия В₆ доминирует над стратегиями В₄, В₅ и В₇. Следовательно, вычеркиваем 4-й, 5-й и 7-й столбцы. Стратегия В₂ доминирует над стратегией В₃. Поэтому 3-й столбец матрицы также можно отбросить.

Оставшаяся матрица

доминируемых стратегий не имеет. Решим игру, заданную матрицей , используя графический метод.

Смешанная стратегия А имеет вид S_A=(p, 1p). Составим функции средних выигрышей игрока А при условии, что игрок В выбирает свои чистые стратегии ,,игре с матрицей:

Н₁=0p+13(1p)=1313p, Н₂=5p+4(1p)=4+p, Н₃=10p+1(1p)=1+9p.

Построим графики этих функций на отрезке р[0, 1].

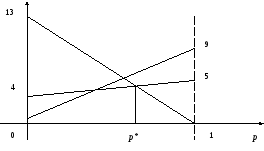
Выделяем нижнюю огибающую этих графиков. Находим самую высокую точку этой огибающей. Эта точка – результат пересечения прямых Н=1313р и Н=4+р. Найдем ее координаты аналитически. Для этого решим уравнение 1313р=4+р. Получим 14р=9, откуда р*=9/140.642, 1р*=5/140.358. Следовательно, оптимальная смешанная стратегия игрока А имеет вид S_A*=(9/14,5/14).

Подставляя значение р*=9/14 в любую из функций Н=1313р или Н=4+р, находим цену игры v_S = 13139/14 = 65/14  4.642.

Нахождение оптимальной стратегии игрока В соответствует случаю 1. Рассмотрим игру 2х2 с матрицей , столбцы которой соответствуют прямым, образующим пик нижней огибающей. Найдем компоненты оптимальной стратегии, воспользовавшись формулами (2.7):

q₁=(45)/(4+0135)=1/140.074, q₂=11/14=13/140.926.

Цена игры =(04+135)/(4+0135)=65/144.642 совпадает с ранее найденной ценой v_S. Учитывая вычеркнутые стратегии игрока В, окончательно запишем оптимальные стратегии игроков для исходной игры S_A*=(9/14,5/14), S_B*=(1/14,13/14,0,0,0,0,0); цена игры v_S=65/14.

Решение игры mх2 производится аналогично. Перечислим лишь основные этапы решения. Пусть исходная игра задается матрицей

.

• Будем искать смешанную стратегию игрока В в виде S_В=(q, 1q)

• Для каждой стратегии А_i игрока А находим средние выигрыши

• H(A_i,S_B)=a_i1q+a_i2(1q) (i=1,2,…,m).

• Строим графики этих выигрышей на координатной плоскости.

• Выделяем верхнюю огибающую построенных графиков, соответствующую наименее благоприятным для игрока В ситуациям.

• Отмечаем точку минимума этой огибающей q*, которая определяет оптимальную стратегию игрока В; при этом сам минимум задает цену игры v.

• В матрице Н оставляем две строки, соответствующие прямым, которые принимали участия в образовании минимума нижней огибающей.

• Для полученной игры 2х2 находим оптимальную стратегию игрока А, применяя формулы (2.7).

• Записываем оптимальную стратегию игрока А, учитывая вычеркнутые строки.