§5. Множество 1. Дополнение.

Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. (Например, киты в классе млекопитающих, множество прямоугольных треугольников в классе треугольников, в геометрии — только множество точек данного пространства, в арифметике — множество чисел).

В настоящем параграфе буквами А, В, С… будем обозначать множества, содержащиеся в некотором фиксированном множестве, которое будем называть пространством или универсумом и обозначать символом 1.

Так как для каждогоА, то

(1)

Множество 1–А называется дополнением множества А и обозначается символом или –А.

.

Очевидно, что (2)

Так как (), то используя формулу (10) §4, получаем закон двойного дополнения:

(3)

Полагая в законах де Моргана (§4, (8)) А=1 и заменяя В и С соответственно на А и В, получаем

(4)

То есть дополнение произведения двух множеств равно сумме их дополнений, а дополнение суммы двух множеств равно произведению их дополнений.

Следует отметить, что формулы, которые мы получаем, введя понятие дополнения, аналогичны законам алгебры высказываний, приведенным в §1. Действительно, достаточно в высказываниях (1) — (4) настоящего параграфа заменить знак равенства (=) знаком эквивалентности () и интерпретировать буквы как переменные высказывания, а символыкак дизъюнкцию, конъюнкцию, ложное высказывание и истинное высказывание (), и мы получим законы алгебры высказываний. И обратно, при соответствующей замене символов в законах алгебры высказываний получаются теоремы алгебры множеств. Учитывая этот факт, отметим, что вычисления для множеств, являющихся подмножествами данного фиксированного множества 1, легчи всего проводить, если при этих вычислениях применяются только операции.

Вычитание (\), можно определить при помощи операции дополнения (–) и одной из операций или. В самом деле,

Отношение включения можно свести к отношению равенства:

(5)

В самом деле, умножая обе части выражения на –В, получаем , откуда следует, что, поскольку.

Обратно, пусть . Тогда:

.

Так как , то из (5) следует, а поскольку изX=0 и Y=0 следует, что , получаем:

(6)

Из (5) легко вывести, что

(7)

Совокупность всех множеств, содержащихся в 1, образует кольцо, если в качестве сложения рассматривать операцию «», а в качестве умножения — операцию «». Это кольцо отличается от кольца множеств, рассмотренного в §5, тем, что оно имеет единицу — множество 1.

В самом деле, равенства (1) показывают, что множество 1 обладает характерным для единицы кольца свойством VIII §5.

Отсюда следует, что вычисления в алгебре множеств можно формально уподобить вычислениям в алгебре чисел.

§6. Конституенты.

В этом параграфе нас будут интересовать множества, получающиеся из производных n множеств при помощи операций сложения (), умножения () и вычитания (\).

Мы покажем, что таких множеств конечное число и что все они могут быть представлены в некотором специальном виде, называемом нормальным.

Пусть ...- произвольные подмножества пространства 1, которое на протяжении всего этого параграфа будет оставаться фиксированным.

Обозначим

для i =1,2,3…n. Очевидно, что

Каждое множество вида

⇋, ()

назовем конституентой (К).

Так как каждый из индексов может принимать только два значения, 0 и 1, то общее число конституент не превосходит.

Например, пусть n=2 и

,

где — зависимые множества.

Итак,

.

Тогда существуют только три конституенты:

, ,.

Рассмотрим свойства конституент.

1. Различные конституенты не пересекаются.

Действительно, если конституенты и, где

,

не совпадают, то , по крайней мере, для одного. Но тогдаи тем более.

2. Сумма всех конституент равна 1.

Для доказательства этого утверждения сначала заметим, что

, а затем раскроем скобки, используя закон дистрибутивного умножения () относительно сложения () (§4, (3)):

конституент,

3. Множество равно сумме конституент, содержащих сомножитель.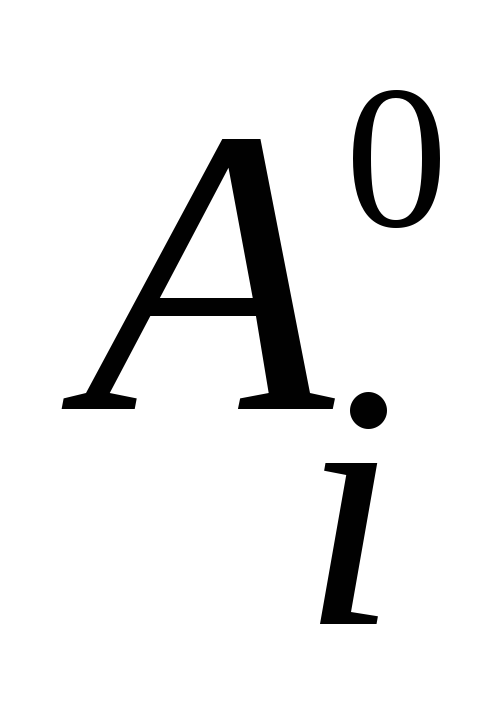

Действительно,

(*), ( h =)

где - все конституенты. Тогда в силу п.1 §6 равенство (*) можем умножить на:

Если () содержит сомножитель, то, так как

Если же содержит, то. Отсюда и следует, чтоявляется суммой тех конституент, которые содержат сомножитель.

Теорема 1. Каждое непустое множество, образованное из множеств при помощи операций сложения (), умножения (), и вычитания (\), является суммой некоторого числа конституент.

Д о к а з а т е л ь с т в о. Теорема верна для множеств . Поэтому достаточно показать, что если множества X и Y являются суммами некоторого числа конституент, то и множества ,,X\Y (если они непустые) можно представить в виде суммы конституент.

Пусть X и Y представимы в виде суммы конституент

Тогда

1. и, значит, является суммой конституент.

Из закона дистрибутивности умножения относительно сложения получим:

2. 

Если , то; в противном случае.

Отсюда и следует, что произведение либо пусто, либо представлено в виде суммы некоторого числа конституент

Если среди конституент встречаются все конституенты, то

3. .

В противном случае пусть — конституенты из ряда (множества), которые не встречаются среди.

Тогда

поскольку ().

Теорема доказана.

Теорема 2. Из n множеств при помощи операций ,и \ можно образовать не более, чеммножеств.

Действительно, каждое такое множество (за исключением пустого), образованное из множеств при помощи операций,и \ , в силу теоремы 1 является суммой конституент, число которых не более. Тогда число различных сумм будет . Важную роль играет частный случай, когда все конституенты отличны от нуля. В этом случае множества называютсянезависимыми.

Теорема 3. Если множества независимы, то число различных конституент равно .

Д о к а з а т е л ь с т в о.

Если ,

(1)

и не все равенства

. . . . . .

верны, то.

Действительно, если, например, ,, то, умножая обе части последнего равенства в (1) на, получаем. Следовательно, если множестванезависимы, то (1) верно только в том случае, когда, что и доказывает теорему.

Пример. Пусть множество составлено из всех таких последовательностей, что каждоеравно либо 0, либо 1, но. Множестванезависимы. Действительно,состоит из всех последовательностей (), для которых, поэтому

.

Применим теперь конституенты для решения следующей проблемы элиминации (лат. eliminatio – исключение, удаление). Введем обозначения:

{А содержит по крайней мере n элементов}

{А содержит точно n элементов}

Пусть - последовательности чисел 0 и 1;

- последовательности неотрицательных целых чисел.

Нас интересует необходимое и достаточное условие существование такого множества X, что утверждения

(I)

справедливы.

Рассуждения:

1. Пусть сначала n = 1. Если вместо запишемi, j, p, q, A, то получим решение:

(II)

Действительно, если существует множество X, удовлетворяющее условиям (I), и i=j=1, то A является суммой двух непересекающихся множеств, имеющих соответственно p и q элементов, а значит, A состоит точно из (p+q) элементов.

Если же , тоА – сумма двух непересекающихся множеств, каждое из которых имеет по крайней мере p (а второе — q) элементов. Тогда А имеет (p+q) элементов. Обратно, если выполнено условие (II), то достаточно в качестве X взять произвольное подмножество множества А, содержащее p элементов.

2. Теперь пусть , и множествапопарно не пересекаются (то есть, (). Сначала потребуем меньшего, а именно, чтобы для каждогоS (S = 1,2,…,n) существовало такое , что

(III)

Как мы уже знаем (см. (II)), для этого необходимо и достаточно, чтобы

для S = 1,2,…,n (IV)

Очевидно, что это необходимое условие того, что существует множество X, удовлетворяющее (I), потому что если такое X существует, то мы можем взять .

Покажем, что это условие является и достаточным. Возьмем в качестве X множество

Тогда (по закону де Моргана)

Так как множества (i =1,2,…,n) не пересекаются, то

, ,

то есть, принимая во внимание (III), убеждаемся, что X удовлетворяет условиям (I).

Предположим теперь, что для каждой пары r, s (1≤r, s≤n) либо, либо.

Обозначим условия (I):

Покажем, что если , то

,

либо ,

либо .

Действительно, если , то

1. , когда

и

2. , когда

Если и, то

1. , когда

и

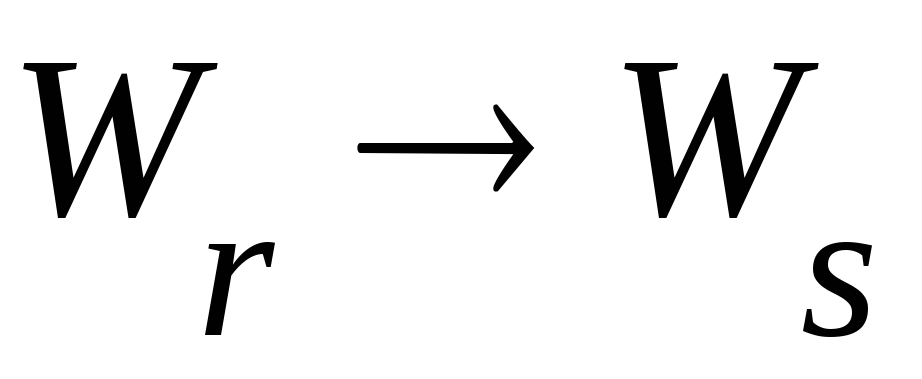2. , когда .

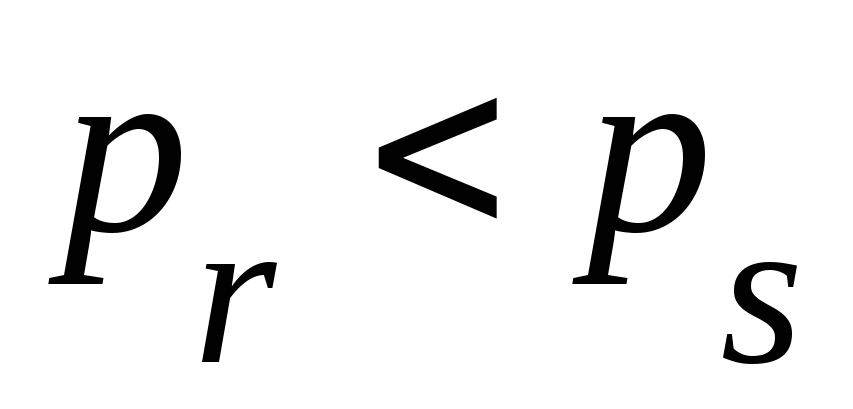Если же , то

1. , когда

и

2. в противном случае ().

Аналогично доказывается, что либо ,

либо ,

либо .

Итак, или конъюнкция условий (I) ложна, или в ней можно опустить некоторые сомножители так, чтобы в полученной эквивалентной конъюнкции никакие два из множеств не повторялись. Таким образом, рассмотренный случай сводится к предыдущему.

Сведем теперь общий случай к случаю, когда множества либо не пересекаются, либо совпадают. В связи с этим заметим, что если, то

Отсюда по индукции получаем, что если множества попарно не пересекаются, то условие видаможно представить в виде дизъюнкции конъюнкций:

.

Представим теперь каждое из множеств в виде суммы конституент. Согласно сделанному выше замечанию, каждое из условий (I) можно представить в виде дизъюнкции некоторых конъюнкций вида

или

.

Используя дистрибутивность конъюнкции относительно дизъюнкции, представим конъюнкцию условий (I) в виде дизъюнкции условий, каждое из которых в свою очередь является конъюнкцией некоторого числа сомножителей вида

или .

При этом отдельные конституенты, входящие в каждую такую конъюнкцию, или совпадают, или не пересекаются, что и сводит этот случай к предыдущему.

Пример. Найти необходимое и достаточное условие существования множества X, для которого

, ,

, .

Эти условия эквивалентны конъюнкции условий

, ,,

, ,,

откуда искомое необходимое и достаточное условие есть

.

Другими словами, конституенты идолжны быть непустыми, а конституентадолжна содержать по крайней мере два элемента.