§4. Свойства симметрической разности.

Симметрическая разность была определена в §2 формулой

(1)

Эта операция обладает свойствами:

1. коммутативности: (2);

2. ассоциативности: (3)

Для доказательства равенства (3) преобразуем его левую и правую части, затем с помощью (8), (9), (10), (11) §4 получим:

Таким образом, множество состоит из элементов, принадлежащихили всем трем множествам А, В, С, или только одному из них.

Чтобы привести к такому же виду правую часть равенства (3), достаточно заметить, что в силу (2):

.

Тогда, заменяя в правой части выражения для буквыА, В, С соответственно на С, А, В получим:

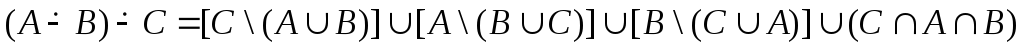, что совпадает с (х).

Из свойства (2), (3) следует, что, принимая операцию «» к конечному числу множеств, можно опускать скобки, указывающие порядок действий.

в) Свойство дистрибутивности:

(4)

Согласно (6) —

(7) —

_{из §4 можем записать:}

У операции «» аналогия с операцией «».

Пустое множество является нулевым элементом (модулем) для операции «», то есть:

(5)

В самом деле, .

Доказанные выше теоремы не позволяют заметить различие между операциями «» и «». Такое различие становится заметным в последующих теоремах. Прежде всего:

(6).

.

Сравнить: .

Операция сложения не имеет обратной.

Выше мы видели, что операция вычитания множеств не является обратной к сложению. Но операция «–» имеет обратную: для произвольных А и С существует одно и только одно такое множество В, что , а именно.

Иначе говоря,

(7)

(8)

В самом деле, из (3), (5), (6) следует, что , что и доказывает (7).

Если же , тои, следовательно,в силу (7).

Таким образом, из (7), (8) следует, что операция «–» имеет обратную и этой обратной операцией является она сама.

В алгебре и теории чисел изучаются совокупности объектов, обычно называемых числами с определенными на них двумя операциями «+» и «» (сложение и умножение), обладающими следующими свойствами:

I. коммутативность;

II. ассоциативность;

3. Существует число 0, такое, что ;

4. Для произвольных x и y существует единственное число (разность) такое, что;

5. ;

6. ;

7. .

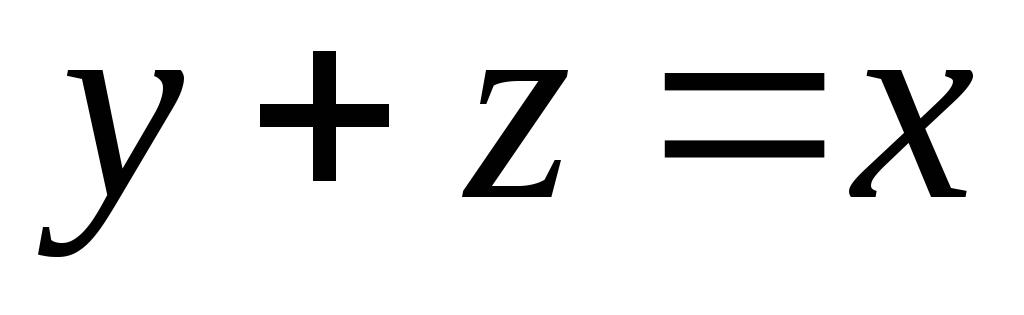Такие совокупности называются кольцами (точнее, абелевыми или коммутативными кольцами).

3. Если существует число 1, такое, что для каждогоx, то говорят, что кольцо имеет единицу или унитарное кольцо.

Алгебраические вычисления в кольцах выполняются точно так же, как в обычной арифметике. При доказательствах правил счета в арифметике, относящихся к сложению, вычитанию и умножению, мы используем только тот факт, что числа образуют коммутативное кольцо с единицей.

Формулы (2) — (8) настоящего параграфа показывают, что множества образуют кольцо (без единицы), если роль «суммы» играет операция «», а роль «произведения» — операция «».

Так как «» не имеет обратной операции, (, но), тоне образуют кольцо (так как условиеIV не выполняется). Но удовлетворяют условиямI — VII.

Если в качестве основных операций применять операции «» и «», то все вычисления в алгебре множеств производятся точно так же, как в обычной арифметике, но при этом можно опускать все показатели степеней, а все коэффициенты приводить по модулю 2 (то есть).

Этот факт имеет тем большее значение, что операции «» и «\» можно выразить через операции «» и «», благодаря чему всю развитую в предыдущих параграфах алгебру множеств можно истолковать в рамках арифметики введенного вышекольца множеств. В самом деле, легко проверить равенства:

(9)

.

Например:

(10)

.

Из (9), (10) следует, что если множества А и В не пересекаются, то

(11)

Применение симметрической разности проиллюстрируем на следующем примере.

Пусть X — множество, J — непустое семейство его подмножеств (то есть множество, элементами которого являются подмножества множества X), удовлетворяющее условиям

(12)

Семейство J, для которого выполнимы эти условия, называется идеалом (J).

Например

.

Пусть

значит J — идеал.

О двух подмножествах А и В множества X говорят, что они равны по модулю J, если . (Например.из предыдущего примера).

Это записывается в виде:

,

или просто , если идеалJ зафиксирован.

Поскольку , то в силу (6)

,

то есть отношение «»рефлексивно (reflexio), обращение назад — одно из свойств отношений, когда каждый элемент множества находится в данном отношении к самому себе (например a=b и ).

Из (2) следует, что , то есть отношение «»симметрично.

Наконец из тождества следует, что, поскольку симметрическая разность двух множеств содержится в их сумме. Тогда в силу (12)

,

то есть отношение «» —транзитивно.

Если заменить в некоторых из предыдущих определений знак «=» знаком «», получим новые понятия. Например, два множества А и В называются непересекающимися по модулю J, если ; множествоА является подмножеством множества В по модулю J, если и тому подобные.