
- •Глава I. Основные понятия…………………………………………. 13
- •Глава I. Основные понятия.
- •§ 1.Множества и операции на множествах.
- •§2. Включение. Пустое множество.
- •Свойства включения.
- •§3. Законы сложения, умножения и вычитания.
- •§4. Свойства симметрической разности.
- •§5. Множество 1. Дополнение.
- •§6. Конституенты.
- •§7. Применение алгебры множеств к отношениям.
- •§8. Булевы алгебры.
- •Int[(a⊙b)](следует из (*))
- •Int[(a⊙b)](b⊙c) (следует из (**))
- •§ 9. Решетки.
- •Глава II. Аксиомы теории множеств. Отношения. Функции.
- •§ 1. Высказывательные функции. Кванторы.
- •§ 2. Аксиомы теории множеств.
- •§ 3. Простейшие следствия из аксиом.
- •§ 4. Декартовы произведения. Отношения.
- •§ 5. Отношение эквивалентности.
- •§ 6. Функции.
- •Функция 2-х и более аргументов.
- •§ 7. Образы и прообразы.
- •§ 8. Функции, согласованные с данным отношением эквивалентности. Булевы факторкольца.
- •§ 9. Отношение порядка.
- •§ 10. Реляционные системы, их изоморфизмы и типы.
§2. Включение. Пустое множество.
О п р е д е л е
н и е 5.
Множество A
называется подмножеством
множества В,
если каждый элемент подмножества А
принадлежит множеству В.
В этом случае мы пишем
![]() или
или![]() и говорим, что множествоА
содержится
в В.
Отношение
и говорим, что множествоА
содержится
в В.
Отношение
![]() называетсяотношением
включения.
называетсяотношением
включения.
Свойства включения.
Из определения
![]() следует:
следует:
![]() (1)
(1)
![]()
Очевидно, что из
![]() следует
следует![]() ,
но не обратно. Если
,
но не обратно. Если![]() и
и![]() ,
тоА
– собственное
подмножество множества
В.
,
тоА
– собственное
подмножество множества
В.
![]()
![]()
Далее
![]() ,
потому что по определению
,
потому что по определению
![]() ,
откуда следует, что
,
откуда следует, что
![]() иА=В
в силу аксиомы J.
иА=В
в силу аксиомы J.
Отношение включения транзитивно:
![]() (2)
(2)
Сумма двух множеств содержит каждое слагаемое:
![]() (3)
(3)
Произведение двух множеств содержится в каждом сомножителе:
![]() (4)
(4)
В самом деле, из
закона
![]() ,
следует, что для каждогоx
,
следует, что для каждогоx
![]()
и, согласно (1) из
§2 ,
![]() ,
а, следовательно, по (1)
,
а, следовательно, по (1)![]() .
.
Второе утверждение в (3) доказывается аналогично.
Для доказательства
(4) нужно использовать закон
![]() .
.

Из (2) §2 следует включение

Отношение включения
можно определить при помощи отношения
равенства и одной из операций
![]() .
.
![]() (5)
(5)
В самом деле, если
![]() ,
то
,
то![]() для каждогоx
и тогда в силу закона
для каждогоx
и тогда в силу закона
![]() имеем:
имеем:
![]() ,
откуда
,
откуда
![]() ,
,
что доказывает,
что
![]() .
.
С другой стороны,
![]() ,
значит
,
значит![]() .
.
Обратно, если
![]() ,
то, согласно (3),
,
то, согласно (3),![]() .
Вторая часть
.
Вторая часть![]() формулы (5) доказывается аналогично.
формулы (5) доказывается аналогично.
Из аксиомы разности (аксиома B §2) следует, что, если существует хотя бы одно множество А, то существует множество А – А, не содержащего ни одного элемента. Такое множество единственно.
В самом деле, если
бы было два таких множества
![]() ,
то для каждогоx
эквивалентность
,
то для каждогоx
эквивалентность
![]()
была бы истинна,
так как оба ее члена ложны. Тогда
![]() в силу аксиомыJ.
в силу аксиомыJ.
Единственное
множество, не содержащее ни одного
элемента, называется пустым множеством
(![]() ).
).
Для каждого x
![]() или
или
![]()
Поскольку импликация с ложной посылкой истинна, для каждого x верна импликация.
![]()
Таким образом, пустое множество является подмножеством любого множества.
Из формулы (1) §2 следует, что
![]()
так как
![]() .
Отсюда заключаем, что
.
Отсюда заключаем, что![]() ,
а из закона
,
а из закона![]()
![]() .
.
Равенство
![]() означает, что множестваА
и В
не имеют общих элементов, то есть не
пересекаются.
означает, что множестваА
и В
не имеют общих элементов, то есть не
пересекаются.
Равенство
![]() означает, что
означает, что![]() .
.
Роль пустого множества в теории множеств аналогична роли числа нуль в алгебре. Без множества 0 операции умножения и вычитания множеств не всегда были бы выполнимы, что в последствии привело бы к значительным трудностям при вычислениях.
§3. Законы сложения, умножения и вычитания.
Операции сложения, умножения и вычитания множеств имеют много общих свойств с операциями сложения, умножения и вычитания чисел.
В этом параграфе приведем важнейшие из них, а также докажем несколько теорем, указывающих на различие между алгеброй множеств и арифметикой.
Законы коммутативности:
 (1)
(1)
Эти законы непосредственно следуют из законов коммутативности для дизъюнкции и конъюнкции.
Законы ассоциативности:
 (2)
(2)
Доказательство основано на законах ассоциативности для дизъюнкции и конъюнкции.
Отсюда следует, что при сложении или умножении конечного числа множеств можно опускать скобки, указывающие порядок действий.
Например: ![]() .
.
Законы дистрибутивности:
 (3)
(3)
Доказательство основано на законах дистрибутивности для дизъюнкции и конъюнкции.
Например: ![]()
Законы идемпотентности:
 (4)
(4) .
.
Доказательства
получаются непосредственно из законов
идемпотентности
![]() ,
,
![]() .
.
Докажем несколько законов для операции вычитания.
 (5)
(5)
сравнить:
![]()
В самом деле, из формул (1) и (2) §2 следует:
 .
.
Откуда по закону дистрибутивности дизъюнкции относительно конъюнкции имеем:
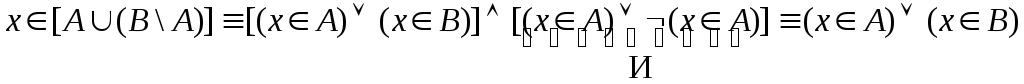 .
.
Поскольку ![]() ,сомножитель И
можно в произведении опустить. Таким
образом получим:
,сомножитель И
можно в произведении опустить. Таким
образом получим:
 ,
,
что и доказывает формулу (5).
Из этой формулы
следует, что вычитание множеств не
является операцией, обратной сложению,
как в обычной алгебре чисел. Если,
например, А
— множество четных чисел, а В
— множество чисел, делящихся на 3, то
множество
 отличается отВ,
потому что оно содержит все четные
числа.
отличается отВ,
потому что оно содержит все четные
числа.
Но если
![]() ,
то (согласно (5) и (5) §3)
,
то (согласно (5) и (5) §3) ,
как в арифметике.
,
как в арифметике.
Далее,
![]() (6).
(6).
![]() ⇋
⇋![]()
В самом деле:

Закон дистрибутивности умножения относительно вычитания имеет вид:
 (7).
(7).
Он получается из эквивалентности
 .
.
Из равенства (7) следует, что
 .
.
Законы де Моргана в алгебре множеств имеют вид:
 (8)
(8)

Доказательство основано на законах де Моргана алгебры высказываний.
П риведем
без доказательств следующие равенства:
риведем
без доказательств следующие равенства:
B
A
C

B
A
C
B
A
C

![]() (12)
(12)

![]() (13)
(13)

 (14)
(14)
Импликации (12) — (14) иллюстрируют аналогию между отношением включения и отношением «не больше» в арифметике.
Из (14) легко следует:
 (15),
(15),
которая имеет свой аналог в арифметике:
![]() .
.
