
книги / Прикладной статистический анализ в горном деле (Одномерная математическая статистика и регрессионный анализ)
..pdf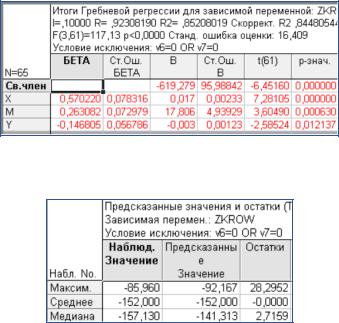
В табл. 6.3–6.6 сравним расчёты обычной и гребневой регрессии для нашего примера с наличием взаимозависимых аргументов.
Таблица 6.3 Итоги гребневой регрессии с включением
Таблица 6.4 Статистики остатков при гребневой регрессии с включением
Анализируя результаты расчётов, можно заметить более высокие результаты значимости коэффициента детерминации и критерия Фишера, полученные по методу «всех регрессий» по сравнению с результатами, полученными по методу «гребневой регрессии с включением». В то же время величина стандартной ошибки оценки и границы разброса остатков больше у метода «гребневой регрессии с включением».
211
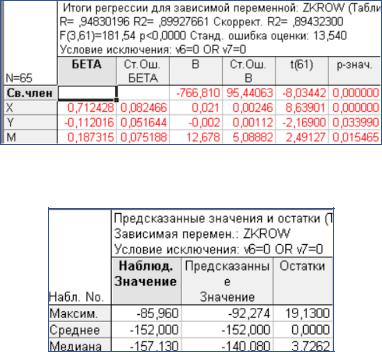
Таблица 6.5 Результаты расчётов по методу всех регрессий:
итоги регрессии
Таблица 6.6
Статистики остатков
Остатки должны быть нормально распределены с нулевым средним. И в первом, и во втором случаях вычисления подтверждают этот принцип. Но медиана от среднего имеет меньшее отклонение в гребневой регрессии, что свидетельствует о большем смещении при использовании метода всех регрессий.
212
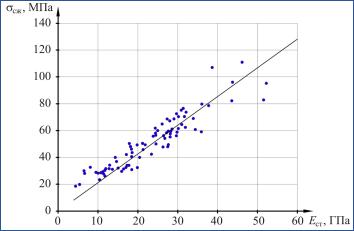
Рис. 6.7. Зависимость статического модуля упругости карбонатных пород в пластовых условиях от скорости продольной волны для месторождений Средней Азии, D = V 2
Множественная регрессия широко используется в науке, её инструменты способствуют более сложному описанию зависимостей. Например, на рис. 6.7 уравнение множественной регрессии показывает зависимость статического модуля упругости карбонатных пород в пластовых условиях от скорости продольной волны для месторождений Средней Азии.
213
7.НЕЛИНЕЙНАЯ РЕГРЕССИЯ
7.1.Виды моделей
Впредыдущих главах при выводе уравнений регрессии мы использовали линейное уравнение, в которое входят в виде суммы произведения i-го коэффициента регрессии на j-й аргумент (раздел 5.2). В реальности в уравнении, помимо суммирования, может использоваться несколько алгебраических операций или их комбинаций. При использовании совокупности разных алгебраических операций можно получить уравнения (регрессионные модели) в разных вариациях:
Уже знакомые нам аддитивные модели, представленные
ввиде алгебраической суммы произведений переменных на вычисленные коэффициенты регрессии при переменных. Они
имеют вид Y = a0 + a1·X1 + a2·X2 + a3·X3 + … + an·Xn.
К таким моделям относится, например, расчёт объема производства готового удобрения в его взаимосвязи с объемом производства хлорида калия в отдельных рудоуправлениях.
Мультипликативные модели, которые представляют собой произведение независимых переменных в степени. Значе-
ниями степеней становятся коэффициенты регрессии. Уравнения имеют следующий вид: Y = а0·Xа1·Xа2·Xа3·…·Xаn.
Примером мультипликативной модели в первых степенях является двухфакторная модель объема валовой продукции (ВП) на обогатительной фабрике рудника: ВП = ЧР·ГВ, где ЧР – численность работников, ГВ – среднегодовая выработка одного работника.
Кратные модели, которые представляют собой частное от деления двух аргументов. Они имеют вид Y = а0·X1а1 / X2а2. Такую модель даёт расчёт рентабельности совокупных активов рудоуправления R, который рассчитывается делением суммы прибыли П на среднегодовую их стоимость С : R = П / С.
214
Смешанные (комбинированные) модели представляют
собой различные сочетания комбинаций предыдущих моделей:
Y = а0· (X1·X2)а2 / X3а3; Y = а0·X1а1×X2а2 / X3а3 и др.
Когда одинаковым приращениям независимой переменной соответствуют неодинаковые и изменяющиеся по некоторому нелинейному закону приращения другого признака, регрессия оказывается нелинейной. Внешним признаком нелинейной регрессии служит то, что средняя линия, построенная на графике рассеивания, формируется в виде кривой различной конфигурации. До этого раздела мы рассматривали линейные регрессионные зависимости и их оценки. Для таких моделей имеются механизмы оценок параметров, разработаны доказательства качества уравнений, развиты методы тестирования и механизмы проверки адекватности. Функции для таких моделей имеют простой вид, их можно достаточно просто реализовать на практике в виде вычислительных алгоритмов. Такие преимущества линейной регрессии делают ее применение более предпочтительным. Когда есть возможность использовать линейную модель с большим количеством переменных вместо нелинейной, пусть даже и с меньшим числом аргументов, лучше предпочесть линейную модель. В реальных случаях использование линейных уравнений для изучения природных и горно-гео- логических зависимостей дает вполне удовлетворительные результаты. Они вполне могут использоваться для создания адекватных зависимостей, выполнения анализа и построения прогноза. Вместе с тем, в силу многообразия и сложности природных условий и процессов, при формировании месторождений не стоит ограничиваться рассмотрением лишь регрессионных моделей линейного вида. К выводу о непригодности модели при проведении анализа линейной регрессии исследователя может привести анализ данных графиков остатков. Нелинейная форма графиков будет свидетельствовать о неадекватности выведенного уравнения и о возможной структуре необходимых нелинейных преобразований.
215
7.2.Виды графиков функций
Вматематике функция – одно из основных понятий, она отражает зависимость одной переменной от другой (или нескольких других). В зависимости от направленности изучаемого явления все семейства функций, используемых в том или ином виде для описания наблюдаемых процессов в природе, можно разделить на несколько крупных категорий:
1. Монотонные. Они могут быть возрастающие и убывающие.
2. С одним или несколькими экстремумами.
3. С изломом.
4. Четные и нечетные.
Монотонные могут быть линейными, степенными (за исключением параболы), показательными, экспоненциальными, логарифмическими и логистическими [51].
Функция является чётной,если для любого значения х из областиопределенияфункциивыполняетсяравенствоf (x)= f (– x).
Функция является нечётной, если для любого значения х из области определения функции выполняется равенство f (– x) =
=– f (x).
7.3.Начальные вопросы спецификации регрессионных моделей
7.3.1. Выбор аргументов и формы уравнения регрессии
Под спецификацией регрессионных моделей понимают выбор аргументов и нахождение вида связи между зависимой переменной и аргументами. Понятно, что для парной регрессии эта задача сводится к выбору аргумента и вида связи. Таким образом, спецификация модели требует решения двух задач. Первая задача – это выбор структуры уравнения регрессии, т.е. ма-
216

тематической формы модели. Вторая – это определение состава независимых аргументов. Качество аппроксимации уравнений регрессии в значительной степени зависит от правильно выбранной спецификации уравнения.
Выбор спецификации должен выполняться на основании глубокого и осмысленного анализа исследуемой задачи, с учётом результатов исследования зависимостей переменных, входящих в восстанавливаемую модель. По мнению авторов работы [1], исследователь ещё до вывода уравнения регрессии должен ответить на ряд вопросов, связанных с характером искомой связи:
–будет выводимая им функция монотонной или она включает экстремумы;
–ожидается ли стремление функции к асимптотам11 и какова их содержательная интерпретация;
–какова природа воздействия независимых переменных на функцию – аддитивная, мультипликативная или иная;
–какова содержательная природа предполагаемой зависимости.
7.3.2. Классы нелинейной регрессии
Построим график рассеивания для содержания двух компонентов (переменных) в горных породах одного из рудников ВКМКС – хлорида калия KCl – и нерастворимого остатка. Рис. 7.1 свидетельствует, что зависимость носит нелинейный характер. Аппроксимация линейным уравнением регрессии (см. рис. 7.1, б) даёт неплохой коэффициент детерминации, но уравнение неадекватно, на это укажет нелинейность графика остатков. Полиномиальное уравнение (см. рис. 7.1, а) нелинейно, имеет высокую степень тесноты связи и адекватно описывает имеющуюся связь.
11 Асимпто́та, или аси́мптота, – прямая, обладающая таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
217
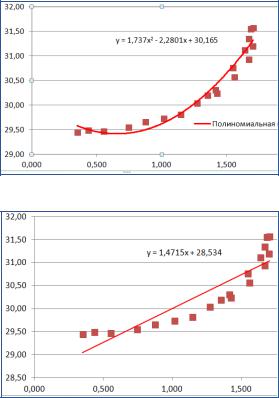
а
б
Рис. 7.1. Уравнения регрессии: а – полином второй степени (R2 = 0,956),
б – линейное (R2 = 0,814)
Если посмотреть на форму уравнений, то на рис. 7.1, б функция линейна, она включает свободный член плюс произведение коэффициента регрессии на аргумент. Уравнение регрессии на рис. 7.1, а включает три слагаемых:
– до преобразований y = a + b1x + b2x2; |
(7.1) |
– после преобразований y = a + b1u1 + b2u2, |
(7.2) |
где a – свободный член, b1, b2 – коэффициенты регрессии,
218
u1 = x; u2 = x2.
В этом уравнении квадратичный аргумент x2 мы заменили на новую переменную u2.
По структуре они оба линейны, и в уравнениях (7.1) и (7.2) произведения b1·x и b2·x2 входят в уравнения аддитивно, как слагаемые. Оно осталось линейным, несмотря на вторую степень у одного из слагаемых. Такие уравнения ещё именуют нелинейными относительно независимых переменных, но они остаются линейными по оцениваемым параметрам, а значит, аддитивными. В этом случае используется обычная замена одних переменных другими. Нелинейные переменные заменяют новыми «линейными» переменными, этот приём и сводит нелинейную регрессию к линейной форме. Мы только преобразовали данные, но с такими данными для построения уравнения регрессии и его оценки можно использовать ранее изложенный метод наименьших квадратов (МНК) [51].
Построим степенную функцию вида
y = axbе. |
(7.3) |
Она нелинейна относительно оцениваемых параметров, так как параметры a и b входят в уравнение не аддитивно, а мультипликативно. К этому же классу можно отнести показательные и экспоненциальные функции. Вместе с тем такая функция становится внутренне линейной, если с помощью соответствующих преобразований её можно свести к линейной форме. Методы преобразований в этом классе регрессий расширены, помимо уже известной замены переменных, можно воспользоваться логарифмированием или иными видами преобразований.
Прологарифмируем выражение (7.3) по основанию e. После логарифмирования получаем линейное по параметрам уравнение, свободный член и коэффициент регрессии которого (а и b) могут быть найдены по МНК:
lnyi = lna + b·lnxi + lnei |
(7.4.) |
(более подробно рассмотрим это в п. 7.5.2.1).
219
Таким образом, различают три класса нелинейных регрес-
сий [1; 51]:
–нелинейные относительно независимых переменных. Такие уравнения остаются линейными по оцениваемым параметрам [1];
–нелинейные по оцениваемым параметрам (их ещё именуют как внутренне линейные);
–нелинейные модели, внутренне нелинейные.
Если нелинейная модель по оцениваемым параметрам линейна, она может быть сведена к линейному виду.
Если нелинейная модель внутренне линейна, после некоторых преобразований её можно привести к линейному виду (например, логарифмированием и заменой переменных).
Если же нелинейная модель внутренне нелинейна, она не может быть сведена к линейной функции.
Для оценки неизвестных параметров в нелинейных моделях как парной, так и множественной регрессии используют замену переменных, логарифмирование всех или некоторых компонентов уравнения или используют эти и другие преобразования в различных комбинациях. Если не удаётся подобрать подходящие преобразования исходных данных, выполняют оценку параметров на основе метода максимального правдоподобия и применения итеративных процедур оптимизации.
7.4. Нелинейная парная регрессия
7.4.1. Степенная функция
Одной из простых и распространенных функций среди степенных является квадратичная с графиком, называемым параболой (рис. 7.2). Крутизна ветвей параболы будет тем выше, чем выше степень(приведеныпримерыдлястепени,равной2и4).
220
