книги / Прикладной статистический анализ в горном деле (Одномерная математическая статистика и регрессионный анализ)

Статистика близка к t-распределению с числом степеней свободы:

В этом случае гипотеза «средние в двух группах равны» принимается, если соблюдается условие

t(n1 n2 2)эмп t( / 2), k .

в) Если дисперсии двух генеральных совокупностей известны, тогда

Известно, что в случае, когда нулевая гипотеза верна, статистика

x y

tэмп Sd

имеет распределение Стьюдента с k-степенями свободы, но для больших выборок (n1 и n2 ) можно воспользоваться нормальной

аппроксимацией.

С помощью вероятностного калькулятора Statistica найдем критическую точку распределения Стьюдента для уровня значимости α / 2 и k = (n1 + n2 – 2) степенями свободы. Обозначим найденную точку через t (α / 2). В этом случае гипотеза «средние в двух группах равны» принимается, если

где t( / 2) – критическая точка распределения Стьюдента.

101

Таким образом, если tэмп < tкрит (для случаев а и б), нулевая гипотеза не может быть отвергнута и различие выборочных

средних считается «статистически незначимым» (при этом обязательно указывается, при каком уровне значимости это имеет место быть).

Если tэмп > tкрит, это означает, что величина d оказалась за пределами своих собственных случайных колебаний. Такое раз-

личие называют «статистически значимым», т.е. нулевая гипотеза должна быть отвергнута. Достоверность в статистическом смысле обозначает, что полученное различие предсказуемо: при повторении эксперимента или наблюдения в тех же условиях оно будет воспроизводиться с вероятностью β или более.

3.4.5. Оценка разности между средними для зависимых (парных) выборок

Вслучае связанных выборок с равным числом измерений

вкаждой из них можно использовать более простую формулу t-критерия Стьюдента.

Всвязанных выборках каждому числовому значению одной выборки обязательно соответствует парное причинно и следственно связанное значение другой выборки. Это имеет место, когда какие-либо характеристики изучаемого явления регистрируются в одном и том же геопространстве, при разных вариантах воздействия. Простейший пример, когда в каждой борозде при опробовании по стенке горной выработки отбирается ряд двойных проб – рядовая и контрольная. Пробы первого типа отправляются в лабораторию 1, а контрольные – в лабораторию 2. Требуется определить качество производства химических анализов разных лабораторий. Формализуем задачу следующим образом.

Пусть имеется совокупность n пар наблюдений (x1, y1), ..., (xn, yn), n – номер бороздовой пробы. Понятно, что каждая пара проб взята из одной точки геопространства, распределение содержания

102

в пространстве равномерное, без выбросов. Поэтому если две лаборатории, выполняя химический анализ по одной методике, дадут одинаковый результат по каждой пробе yi = xi, i = 1, n, то качество их работы одинаково высокое. Учитывая наличие погрешностей в процессе анализа, результаты анализов могут расходиться. Составим разности di = yi − xi, i = 1, n и проверим

гипотезу о равенстве нулю среднего разностей d , H0: d = 0 про-

тив альтернативы H1: d ≠ 0. В примере предполагается равномерное(безналичияэффектасамородков7)распределениекачества.

Дляпроверкигипотезыприменяетсяследующаястатистика:

tэмп Sd d/ n ,

где d – разность между двумя значениями в одной паре,

d – выборочное среднее для парных разностей,

Sd – стандартное отклонение разностей для выборки, n – количество пар.

Стандартное отклонение разностей для выборки вычисляется по одной из формул:

где Sd – стандартная ошибка, или мера отклонения наблюдаемой разницы выборочных средних от теоретически возможной, «генеральной». Формально величина t показывает, во сколько раз

7 Эффект самородка (nugget effect ) используется в тех случаях, когда экспериментальные данные измерены в точках не точно, а с некоторой погрешностью. Например, из одной пробы отобраны две навески и отправлены для анализа в две разные лаборатории. Получили два различных значения содержания. Разность между ними составляет эффект самородка. Причиной разности может быть и крайне неравномерное распределение полезного ископаемого, например пробы по рассыпному золоту.

103

разница выборочных средних превышает свою собственную случайную вариацию.

Пример. По одной из горных выработок отрабатываемой панели отобраны 10 двойных проб (табл. 3.6). Рядовые пробы направлены в первую лабораторию, а контрольные во вторую. Требуется определить, значимо ли различие в результатах анализов нерастворимого остатка у двух лабораторий на уровне значимости 0,05. Разности содержаний нерастворимого остатка NO результатов анализов первой и второй лаборатории вычислим из выражения:

di = NO1i – NO2i.

Сформулируем основную и альтернативную гипотезы: H0: d = 0 против альтернативы H1: d ≠ 0, для проверки гипотезы используем t-статистику.

Выборочное среднее для парных разностей: d =

104

Вычисляем эмпирическое значение статистики t:

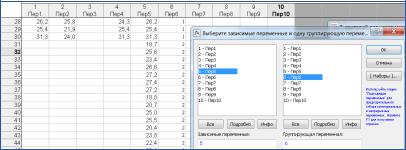
В программе Statistica по вероятностному калькулятору рассчитываем критическое значение для α / 2 = 0,025 и число степеней свободы n – 1 = 9 (рис. 3.9). Критическая область является двусторонней.

Рис. 3.9. Окно программы Statistica для вычисления критического параметра t-критерия Стьюдента

Поскольку |tэмп| < tкрит, основная гипотеза не отвергается, различие в результатах анализов нерастворимого остатка у двух лабораторий на уровне α = 0,05 незначимо.

Считается, что t-критерий может использоваться и для выборки очень небольшого размера, даже в пределах 10 наблюдений. Желательно выполнять проверку условия о нормальном распределении выборок. Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограмм) или применяя критерий нормальности. Вместе с тем эффективно проверить гипотезу о нормальности можно только для достаточно большого объема данных.

105

Более осторожно нужно подходить к различию дисперсий сравниваемых групп. Равенство дисперсий в двух группах можно проверить с помощью F-критерия (который включен в вероятностный калькулятор программы Statistica). Также можно воспользоваться более устойчивым критерием Левена [65].

3.4.6.Пример выполнения оценки разности средних

идисперсий для независимых выборок в программе Statistica

Для примера произведём оценку разности средних и дисперсий для независимых выборок с использованием программы

Statistica.

Пример. На северной и южной полупанелях сильвинтового пласта АБ отобраны пробы по полезному компоненту КCl. Результаты анализа по 30 пробам каждой полупанели отображены в таблице рис. 3.10 (пер. 1 – северная часть панели, пер. 2 – южная). Требуется установить, однородны ли данные по северной и южной частям панели.

Рис. 3.10. Выбор переменных

Воспользуемся встроенным модулем «Основные статистики и таблицы» (Basic Statistica / Tables)» из вкладки меню «Анализ».

106

.

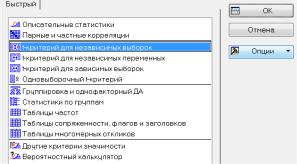
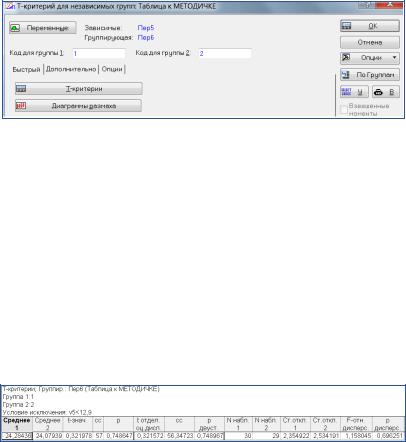
Рис. 3.11. Выбор команды для проверки независимости данных

В открытом списке задач имеются две строки с одинаковыми возможностями (рис. 3.11). Если использовать пункт «t- критерий для независимых переменных» (t-test for independent variables), потребуется, чтобы данные были размещены в двух столбцах. Теоретически t-критерий может применяться только в том случае, если переменные нормально распределены. Но во второй переменной анализируемой панели имеется выброс, который требуется исключить на время анализа (проба № 53, прил. А). В случае физического удаления выброса из таблицы из анализа будет исключена вся строка включая значение первой переменной, в которой отсутствует выброс. Поэтому целесообразно исключить выброс из анализа, не удаляя его из таблицы. Для этого используем опцию программы Statistica – Select cases.

Воспользуемся возможностями команды, зашитой в строке «t-критерий для зависимых переменных» (t-test for dependent variables). Для этого организуем две новые переменные и увеличим количество наблюдений до 59 (30 + 29 = 59). В первую новую переменную скопируем все данные из первого столбца и во второй переменной введём для них ключ, равный единице. Скопируем все данные второго столбца и вставим их в первый новый столбец в продолжение имеющихся данных. Во втором новом столбце поставим у вновь скопированных данных ключ, равный двум (см. рис. 3.10).

107

Таким образом, в новых переменных появились все данные из первой и второй переменных, но их можно отличить значениями ключа.

В первой половине открытого окна выбираем первый новый столбец 5, а во второй половине окна группирующую переменную 6, которая является ключом (см. рис. 3.10).

Прописываем ограничение по минимальному значению – кнопка Select cases (рис. 3.12).

Рис. 3.12. Окно задания условия ограничения

Далее переходим на вкладку «Опции» (Options), отмечаем галочкой строку t-критерий с разделенными оценками диспер-

сий (t-test with separate variance estimates) и указываем значение р-уровня (рис. 3.13).

Рис. 3.13. Условия выбора опций

Также опции позволяют отображать длинные имена переменных, задавать уровень значимости и использовать два дополнительных критерия для сравнения дисперсий – Левена

(Levene’s test) и Брауна – Форсайта (Brawn & Forsythe test).

108

Равенство дисперсий в двух переменных можно проверить с помощью F-критерия, он включен в таблицу вывода результатов. В качестве опций возможен расчет t-критерия как с объединением дисперсий (по умолчанию), так и с раздельным их рас-

четом (t-test with separate variance estimates). Первый из этих случаев возможен, когда дисперсии обеих выборок однородны, а второй – когда неоднородны.

Вернёмся на вкладку «Быстрый» (рис. 3.14) и произведем расчеты, нажав на клавишу «T-критерий» (Summary: t-test).

Рис. 3.14. Окно выбора кодов с активной вкладкой «Быстрый»

Врезультате расчетов появится табл. 3.7, в которой указано два варианта расчета числа степеней свободы и уровней значимости для проверки гипотезы о равенстве средних – для случая однородных (t-значение, степени свободы, p) и неоднородных дисперсий (t-значение, степени свободы, p двусторонний).

Втабл. 3.7 pдисперс – вероятность ошибки для F-теста Фишера. Поскольку в нашем случае р > 0,05, можно заключить, что

дисперсии сравниваемых выборок не различаются (т.е. условие однородности дисперсий выполняется).

Таблица 3.7

Результаты вычисления данных к гипотезе о равенстве средних

109

Под однородностью понимается их статистическая неразличимость. В первом случае, когда выборки имеют равные средние и равные дисперсии, число степеней свободы равно сумме объемов двух выборок минус два, в нашем примере (30 + 29) – 2 = 57. Если гипотеза о равенстве средних отвергается с заданным в опциях уровнем значимости, то цифры в выведенной таблице будут показаны красным цветом. Возможен второй случай, когда гипотеза о равенстве средних не отвергается, а дисперсии сравниваемых выборок статистически отличаются. В программе Statistica, в такой ситуации число степеней свободы будет скорректировано, оно будет тем меньше, чем больше отличаются дисперсии. В таблице скорректированное число степеней свободы 56,35. Коррекция проводится аналитически, поэтому и появляется дробное число. Уровень значимости для t-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве средних двух выборок, когда в действительности эта гипотеза имеет место быть.

Из таблицы видно, что и средние значения, и дисперсии по полупанелям отличаются незначительно. Проверим расчёты по первому варианту. Вычисленное значение (эмпирическое) мень-

ше критического tэмп(57; 0,74) = 0,32 < ǀ t(57; 0,05)ǀ = 1,67 (рис. 3.15),

можно сделать предположение о принятии нулевой гипотезы, о равенстве средних двух выборок.

Достигаемый уровень р-значимости критерия Стьюдента 0,75. В этом анализе он равен вероятности ошибки принять гипотезу о неравенстве средних, когда в действительности средние равны. Для варианта с раздельным расчетом дисперсий незначительно уменьшилось число степеней свободы (с 57 до 56,34), а остальные статистики изменились незначительно.

Проверка равенства дисперсий проводится по отношению дисперсий выборок. Оно составляет Fэмп = 1,16. Критическая величина критерия Фишера определяется в статистическом калькуляторе. Как указывалось, в системе Statistica реализован односторонний критерий Фишера, т.е. в числителе

110