
книги / Пьезокомпозиты и датчики в 3 ч. Ч. 1 Статистическая механика пьезокомпозитов
.pdf
рис. 1.1, б, в соответственно; для гранулированного композита – из решения задачи о нагружении составной сферы (см. рис. 1.1, з).
Например, для поперечных диэлектрических проницаемостей *(1)11,*(2)11 однонаправленного двухфазного волокнистого композита [104]
|
|
|
|
|
v2 |
|
|
= |
|
v1 |
|
− |
1 |
, |
||||||
|
|
|
|
* |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
− |
(1)11 |
|
2 |
(1)11 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(1)11 |
|
|
|
|
|
|
|
11 |
(2.3) |
|||||||||||
|
|
|
|
|
v1 |
|
|
|
|
|
v2 |
|
1 |
|||||||
|
|
|
|
|
|
|
|
= |
|
+ |
|
, |
||||||||
|
|
|
* |
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
− |
(2)11 |
|
|
(2)11 |
|
|
|||||||||||
(2)11 |
|
|
|
|
|
|
11 |
|
|
|||||||||||
где |
|
11 = (1)11 − (2)11 , v2 |
=1− v1 ; |
для продольной диэлектрической |
||||||||||||||||
|
||||||||||||||||||||
проницаемости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
*(1)33 |
= *(2)33 = |
33 . |
(2.4) |
||||||||||||
Для полидисперсной волокнистой структуры (см. рис. 1.1, д) с трансверсально-изотропными диэлектрическими проницаемостями обеих фаз решение для эффективной диэлектрической проницаемости в плоскости изотропии r1r2
* |
= * |
= |
1 |
(−b |
|
) |
(2.5) |
|
D |
||||||||
|
||||||||
22 |
11 |
|
2a |
|
||||
|
|
|
|
|||||
может быть получено из расчетной схемы: одиночное волокно с прослойкой матрицы толщиной в эффективной среде [34],
нагруженной поперечным, например вдоль оси r1, электрическим полем – как решение квадратного уравнения
a 11*2 + b 11* + c = 0,
в решении (2.5) которого
D = b2 − 4ac, a = b0 , b = a0 − b0 (2)11 − 4v1 11 , c = −a0 (2)11 ,
a0 = (1)11 + (2)11 + v0 11, b0 =1+ v0 + (1− v0 ) (1)11 / (2)11,
71

разность 11 = (1)11 − (2)11, диэлектрические проницаемости фаз
(1)11 , (2)11. Для случая, показанного на рис. 1.1, г, с отсутствием прослойки ( = 0) необходимо в решении (2.5) для эффективной
диэлектрической проницаемости * коэффициенты задать в виде |
|||||||||||
|
|
|
|
|
|
|
11 |
|
|
|
|
a =1, |
b = |
|
11(1− 2v1) , |
c = (1)11 (2)11. |
|
||||||
|
|
||||||||||
Для всех структур (см. рис. 1.1, б–д) эффективная продольная |
|||||||||||
диэлектрическая проницаемость |
|
|
|
|
|
||||||
* |
|
= |
33 |
= v |
(1)33 |
+ v |
(2)33 |
(2.6) |
|||
33 |
|
|
|
1 |
|
2 |
|
||||
совпадает с решением Фойгта и не зависит от толщины прослойки, оператор осреднения по объему композита 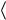 ...
... .
.
Формула Максвелла – Гарнета [9; 95] для эффективной диэлектрической проницаемости *33 двухфазного композита с эллипсоидальными включениями, главные полуоси которых a = b c ,
* |
|
|
v1 |
|
|
|
|
|
= |
1+ |
|
|
|
|
(2.7) |
||
|
|
|
|
|||||
|
|
|
||||||
33 |
|
(2)33 |
|
|
|
|
|
|
|
|
|
v2 A3 + (2)33 |
/ 33 |
|
|||
полуось c ориентирована вдоль оси r3 ; фактор деполяризации эллипсоида [9]
|
|
0 A3 ( ) 1 |
|
|
|
|||||||
для случая c / a 1: |
|
|
|
|
|
|
|
|
|
|
|
|
A = |
1− e2 |
1 |
ln |
1+ e |
− e |
|
, |
|||||
|
3 |
|
|
|
|
|
|
|||||
|
|
|
||||||||||
3 |
e |
|
|
|
|
|
||||||
|
|
2 |
|
|
1− e |
|
|
|
||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
e = |
1−1/ 2 ; |
|
|
|
|||||||
для случая 1:
72

A |
= |
1+ t2 |
[t − arctgt], |
|||
t3 |
||||||
3 |
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|||
|
t = 1/ 2 −1. |
|||||
В частных случаях: для «игольчатых» включений 1 |
||||||
|
|
A ln / 2 |
||||
|
|
3 |
|
|
|
|
и при → имеем A3 → 0 ; для шара =1 |
||||||
|
|
A3 =1/ 3; |
||||
для «сплюснутых» включений |
1 |
|
||||
A3 1− / 2
и при → 0 имеем A3 →1. Отметим, что для однонаправленного
волокнистого композита из формулы Максвелла – Гарнета (2.7) следует решение Фойгта (2.1).
В общем случае задача прогнозирования эффективных физи- ко-механических свойств композита сводится к постановке и решению соответствующих краевых задач для представительной микронеоднородной области V композита.
2.1. Определяющие соотношения на микро- и макроуровнях композита. Постановка связанной
краевой задачи электромагнитоупругости на микроуровне композита
Ненулевые компоненты рассматриваемых трансверсальноизотропных тензоров: упругих C, пьезоэлектрических e и пьезо-
магнитных h свойств, диэлектрических λ и магнитных μ проницаемостей, электромагнитных связанностей κ, температурных ко-
73
эффициентов β, пироэлектрических π и пиромагнитных постоянных представим в матричной форме записи
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c11 |
|
|
|
|
|
c12 |
c13 |
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c12 |
|
|
|
|
|
|
c11 |
c13 |
0 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cij |
|
= |
|
c13 |
|
|
|
|
|
|
c13 |
c33 |
0 |
|
|
0 |
0 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
c |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
|
c44 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
|
|
0 |
|
c66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 0 0 e15 |
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
0 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
eij |
= |
|
|
|
|
0 |
0 |
|
|
0 |
e15 |
0 |
|
0 |
|
|
|
, |
|
ij |
= |
0 |
|
|
1 |
0 |
|
|
|
, (2.8) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e31 |
|
|
e31 |
e33 |
0 0 0 |
|
|
|
|
|
|
|
|
|
0 0 3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
0 h14 |
h15 |
0 |
|
|
|
|
|
|
1 |
0 0 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
hij |
|
|
|
= |
|
0 |
0 |
|
|
|
0 h15 |
−h14 |
|
|
|
|
, |
|
ij |
|
= |
0 1 |
0 |
|
|
|
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
h31 |
|
|
h31 |
h33 |
0 |
0 0 |
|
|
|
|
|
|
0 0 3 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
12 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = |
|
11 |
−12 |
0 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
ij |
|
|
|
|
|
− |
|
|
|
0 |
|
|
|
|
|
|
|
, |
|
ij |
|
|
|
|
|
ij |
|
|
|
|
|
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
0 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
33 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
0 |
|
0 |
|
|
|
, |
{ |
} = |
0 |
|
, |
|
{ } = |
0 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ij |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||
или через разложения
Cijmn = c12 ij mn + c66 ( im jn + in jm ) +
+(c11 + c33 − 2c13 − 4c44 ) i3 j3 m3 n3 +
+(c13 − c12 )( i3 j3 mn + ij m3 n3 ) +
+(c44 − c66 )( i3 m3 jn + j3 n3 im + i3 n3 jm + j3 m3 in ) ,
74
ekmn = e31 k 3 mn +
+(e33 − e31 − 2e15 ) k 3 m3 n3 + e15 ( kn m3 + km n3 ),
kn = 1 kn + ( 3 − 1 ) k 3 n3 ,kn = 1 kn + ( 3 − 1 ) k 3 n3 ,
k = 3 k 3 ,
где c66 = (c11 − c12 ) / 2, символы Кронекера
|
1, |
i = j, |
(2.9) |
ij |
= |
i j, |
|
|
0, |
|
тензорные и матричные индексы связаны между собой соотношения-
ми: 11→1, 22 → 2 , 33 → 3, 23 и 32 → 4 , 13 и 31→5 , 12 и 21→ 6.
Независимые компоненты тензоров упругих C , диэлектрических λ и пьезоэлектрических e свойств некоторых пьезоэлектрических материалов, в частности, трансверсально-изотропных керамик PZT, ЦТС, полимера PVDF, даны в [5; 29; 76; 102] с учетом равенств
Cijmn = Cmnij = Cjimn = Cijnm , eimn = einm , ij = ji ,
C2222 = C1111, C2233 = C1133 , C2323 = C1313 , C1212 = (C1111 −C1122 ) / 2 , e322 = e311 , e223 = e113 , 22 = 11 .
Пироэлектрический эффект имеет трансверсально-изотроп- ный пьезоэлектрик титанат бария с независимыми компонентами тензоров пьезоэлектроупругих свойств [9]:
C |
=16,80 1010 Па, |
C = 7,82 1010 , |
C |
= 7,10 1010 |
Па, |
|||||||||
1111 |
|
|
|
|
|
|
1122 |
|
|
|
|
1133 |
|
|
|
C |
|
|
=18,90 1010 Па, |
C |
|
= 5,46 1010 Па, |
|
||||||
|
3333 |
|
|
|
|
|
1313 |
|
|
|
|
|||
e |
=11,6 |
Кл/м2, |
e |
|
= −4,40 Кл/м2, |
e =18,6 Кл/м2, |
(2.10) |
|||||||
113 |
|
|
|
311 |
|
|
|
|
|
333 |
|
|
||
|
|
|
=112 10−10 Ф/м, |
|
33 |
=126 10−10 |
Ф/м, |
|
||||||
|
11 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= 2,18 106 |
Па/○К, |
|
|
=1,95 106 |
Па/○К, |
|
||||||
|
11 |
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
=19 10−5 |
Кл/○Км2. |
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
75

Пьезомагнитный эффект проявляется у трансверсальноизотропного феррита [102], изотропные упругие свойства которого заданы через независимые компоненты тензора упругих свойств
C |
= 22 1010 Па, C |
= 5,5 1010 Па, |
(2.11) |
1111 |
1212 |
|
|
трансверсально-изотропные магнитные свойства с осью симметрии r3 заданы через пьезомодули
h311 = h322 = −400 Тл, |
h333 = 800 Тл, h113 = h223 = 200 Тл, |
|
||||||
|
|
|
h123 = −h213 =100 |
Тл |
|
(2.12) |
||
и магнитные проницаемости |
|
|
|
|
||||
|
= |
22 |
= 3,14 10−5 |
Тл.м/А, |
33 |
= 2,51 10−5 |
Тл.м/А. |
(2.13) |
11 |
|
|
|
|
|
|
||
Возможны разложения рассматриваемых трансверсально изотропных тензоров
Cijmn = c12 ij mn + c66 ( im jn + in jm ) ,
ekmn = e31 k 3 mn +
+(e33 − e31 − 2e15 ) k 3 m3 n3 + e15 ( kn m3 + km n3 ) ,
hkmn = h31 k 3 mn +
+(h33 − h31 − 2h15 ) k 3 m3 n3 + h15 ( kn m3 + km n3 ) + (2.14) +h14[ k1( m2 n3 + m3 n2 ) − k 2 ( m3 n1 + m1 n3 )],
kn = 1 kn + ( 3 − 1 ) k 3 n3 , kn = 1 kn + ( 3 − 1 ) k 3 n3 ,kn = 1 kn + ( 3 − 1 ) k 3 n3 ,
k = 3 k 3 , k = 3 k 3
с учетом связи c12 = c11 − 2c66 .
Представительная область V композита состоит из однородных трансверсально-изотропных пьезоэлектромагнитных фаз, плоскости изотропии которых лежат в координатной плоскости
r1r2 , ось поляризации r3 . Для области V задан тензор однородной макродеформации ε* , векторы однородных макронапряженностей электрического E* и магнитного H* полей и однородное прира-
76

щение температуры , вызванное внешним нагревом. Выполня-
ются условия идеального контакта на межфазных поверхностях: непрерывность векторов перемещений, напряжений, индукций электрического и магнитного полей.
На структурном или «микро-» уровне представительной области V композита определяющие соотношения
ij = C( f )ijmn mn |
− e( f )nij En |
− h( f )nij Hn |
− ( f )ij , |
|
|
Di |
= e( f )imn mn |
+ ( f )in En |
+ ( f )in Hn |
+ ( f )i , |
(2.15) |
Bi |
= h( f )imn mn |
+ ( f )in Hn |
+ ( f )in En |
+ ( f )i |
|
связывают напряжения σ, |
индукции электрического D и магнит- |
||||
ного B полей с деформациями ε , напряженностями электрического E и магнитного H полей через считающиеся известными для каждой фазы f тензоры упругих свойств C f , пьезоэлектрических
e f и пьезомагнитных h f свойств, диэлектрических λ f |
и магнит- |
|
ных μ f проницаемостей, электромагнитных связанностей χ f |
, κ f , |
|
температурных коэффициентов β f , пироэлектрических |
π f |
и пи- |
ромагнитных f постоянных фаз. |
|
|
В микронеоднородной представительной области |
V компо- |
|
зита поля пьезоэлектромагнитных свойств имеют вид |
|
|
C(r)λ(r)μ(r)e(r)( )h r =χ(r)κ(r)β(r)π(r)(r)
|
C f |
|
|||
|
|
λ |
|
|
|
|
|
|
f |
|
|
|
|
μ f |
|
|
|
|
|
|
|
|
|
|
e f |
|
|
||
F |
|
|
|
|
|
|
h f |
|
(r) , |
||
|
χ |
|
i f |
||
f =1 |
|
|
f |
|
|
|
κ |
f |
|
|
|
|
|
|
|
|
|
|
β f |
|
|||
|
|
|
|
||
|
|
π |
f |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
if |
1, |
r Vf |
(2.16) |
(r) = |
r Vf |
||
|
0, |
|
77

Тензоры эффективных свойств композита: C* , λ* , μ* , e* ,
h* , χ* , κ* , β* , π* , * |
входят в определяющие соотношения на |
||||||
макроуровне композита |
|
|
|
|
|
|
|
*ij |
= Cijmn* |
*mn |
− enij* |
En* − hnij* Hn* − *ij , |
|
||
Di* = eimn* *mn |
+ *in En* + *in Hn* + *i , |
(2.17) |
|||||
B* = h* |
* |
+ * |
H * + * |
E* |
+ * |
|
|
i |
imn |
mn |
in |
n in |
n |
i |
|
и связывают осредненные или макроскопические значения напря-
жений |
σ* = σ , |
деформаций |
ε* = ε , |
индукций |
D* = D , |
||||||
B* = B |
и напряженностей E* = E , |
H* = H |
и в общем случае |
||||||||
рассчитываются по формулам |
|
|
|
|
|
|
|
||||
|
Cijmn* |
= Cijdb Adbmn − epij Fpmn(1) − hpij Fpmn(2) |
, |
|
|||||||
|
*kn |
= kp H pn(1) |
+ kp H pn(2) |
+ ekpq Bpqn |
, |
|
|||||
|
*kn |
= kp M pn(1) |
+ kp M pn(2) |
+ hkpq Dpqn |
, |
|
|||||
|
enij* |
= epij H pn(1) |
+ hpij H pn(2) |
− Cijpq Bpqn |
, |
|
|||||
|
hnij* = epij M pn(1) |
+ hpij M pn(2) |
−Cijpq Dpqn |
, |
|
||||||
|
*kn = |
kp M pn(1) + kp M pn(2) + ekpq Dpqn |
, |
(2.18) |
|||||||
|
*kn |
= kp H pn(1) |
+ kp H pn(2) |
+ hkpq Bpqn |
, |
|
|||||
|
*ij = |
ij |
+ −CijdbTdb + epijTp(1) |
+ hpijTp(2) , |
|
||||||
|
*i |
= |
i |
+ ipTp(1) |
+ ipTp(2) |
+ eipqTpq |
, |
|
|||
|
*i |
= |
i |
+ ipTp(1) |
+ ipTp(2) |
+ hipqTpq |
, |
|
|||
где A(r) , B(r) ,…, T(2) (r) – коэффициенты разложений
78

ij (r) = Aijmn (r) *mn + Bijn (r)En* + Dijn (r)Hn* +Tij (r) ,
Ei (r) = Fimn(1) (r) *mn + Hin(1) (r)En* + Min(1) (r)Hn* +Ti |
(1) (r) , |
(2.19) |
|
Hi (r) = Fimn(2) (r) *mn + Hin(2) (r)En* + Min(2) (r)Hn* +Ti |
(2) (r) |
|
|
полей деформаций ε(r) , электрической E(r) и магнитной H(r)
напряженностей в представительной области композита V . Определяющие соотношения для пьезоактивных сред,
например на макроуровне композита (2.17), можно записать в виде
*ij = Sijmn* *mn + dnij* En* + bnij* Hn* + *ij ,
Di* = dimn* *mn |
+ in( )*En* + in( )*Hn* + i( )* , |
(2.20) |
Bi* = bimn* *mn |
+ in( )*Hn* + in( )*En* + i( )* , |
|
где тензоры эффективных упругих податливостей S* C*−1 и пьезоэлектромагнитных свойств
|
|
|
dnij* |
Sijpq* |
enpq* |
, |
bnij* |
Sijpq* |
hnpq* |
, |
*ij |
Sijpq* *pq , |
|
|
|
|
|||||||
( )* |
|
* |
|
* |
* |
, |
( )* |
|
|
* |
* |
* |
, |
( )* |
|
* |
* |
* |
|
, |
(2.21) |
||
in |
= in |
+ eipq dnpq |
in |
in + eipqbnpq |
i |
|
i + eipq |
pq |
|||||||||||||||
( )* |
|
* |
|
* |
* |
|
( )* |
|
* |
|
* |
* |
, |
( )* |
* |
|
* |
|
|
* |
|||
in |
|
= in |
+ hipqbnpq , |
in |
|
in |
+ hipq dnpq |
i |
|
i |
+ hipq |
pq |
|||||||||||
при σ* = 0 .
Постановка связанной краевой задачи электромагнитоупругости на микроуровне композита. Постановка связанной краевой задачи электромагнитоупругости для структурно неоднородного тела V с границей Γ состоит из уравнений равновесия
ij, j (r) = 0 , |
(2.22) |
непрерывности |
|
Di,i (r) = 0 , Bi,i (r) = 0 , |
(2.23) |
физических соотношений (2.15), соотношений Коши малых упругих деформаций
79

|
|
|
ij (r) =[ui, j (r) + u j,i (r)] / 2 , |
|
(2.24) |
||||||
связи напряженностей |
|
|
|
|
|
|
|
|
|||
|
|
|
Ei (r) = −,i (r) , |
Hi (r) = −,i (r) |
|
(2.25) |
|||||
с потенциалами электрического (r) и магнитного |
(r) |
полей и |
|||||||||
граничных условий, например, вида |
|
|
|
|
|
||||||
|
u |
|
= u* (r) , |
|
|
= * |
(r) , |
|
= * (r), |
|
(2.26) |
|
i |
i |
|
|
|
|
|
|
|||
где σ(r) , ε(r) |
и u(r) – поля напряжений, деформаций и переме- |
||||||||||
щений, D(r) , |
E(r) , (r) |
и B(r) , |
H(r) , |
(r) – поля индукций, |
|||||||
напряженностей и потенциалов электрического и магнитного полей, u* (r) , * (r) , * (r) и – заданные значения полей переме-
щений, электрического и магнитного потенциалов на границе и температура внешнего нагрева представительной области V . Выполняются условия идеального контакта на межфазных поверхностях: непрерывность векторов перемещений, напряжений, индукций электрического и магнитного полей в представительной области композита V .
Таким образом, вычисление тензоров C* , …, * (2.17),
(2.20), (2.21) эффективных свойств пьезокомпозита в общем случае сводится к решению связанной стохастической краевой задачи электромагнитоупругости с быстро осциллирующими коэффициентами (2.15) в представительной области V с границей Γ
[Cijmn (r)um,n (r)], j +[enij (r) ,n (r)], j +[hnij (r) ,n (r)], j −[ ij (r)], j |
= 0, |
|||||||||||||
[ejmn (r)um,n (r)], j |
−[ jn (r) ,n (r)], j |
+[ j (r)], j = 0 , |
(2.27) |
|||||||||||
[hjmn (r)um,n (r)], j |
−[ jn (r) ,n (r)], j +[ j (r)], j = 0 ; |
|
||||||||||||
u |
|
= * r |
j |
, |
|
|
= −E*r |
j |
, |
|
|
= −H *r |
j |
|
i |
ij |
|
|
j |
|
|
j |
|
||||||
для полей перемещений u(r) , электрического (r) |
и магнитного |
|||||||||||||
(r) потенциалов. Эти поля в силу линейности задачи (2.27) будут
80
