
книги / Пьезокомпозиты и датчики в 3 ч. Ч. 1 Статистическая механика пьезокомпозитов
.pdf
ячейками: коррелированными полидисперсными (см. рис. 1.18, б) (случайное взаимное расположение центров сечений волокон которых совпадает с расположением центров сечений волокон в начальной полидисперсной структуре III, (см. рис. 1.18, а) или монодисперсными (с квазипериодическим расположением в узлах гексагональной решетки, см. рис. 1.18, г) составными ячейками заполнено некоррелированными по размерам и взаимному расположению такими же, но, например, бесконечно малыми составными ячейками. Величины, относящиеся к коррелированным полидисперсным структурам (см. рис. 1.18, б, г), обозначим верхним индексом « I' ».
Радиусы «привязанных» составных ячеек в коррелированных полидисперсных структурах (см. рис. 1.18, б, г) попарно совпада-
ют, а радиусы расположенных в них волокон rI' |
rIII . Коэффици- |
||||
ент корреляции коррелированных |
полидисперсных структур III |
||||
(см. рис. 1.18, а) и I’ (см. рис. 1.18, б) |
|
|
|
|
|
p = |
p0 − v1 |
, |
|
|
(1.105) |
1− v |
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
|
так как для рассматриваемых структур v |
= p v с учетом rI' |
rIII . |
|||
|
|
11 |
0 1 |
|
|
а |
б |
в г
Рис. 1.18. Фрагменты реализаций коррелированных полидисперсных структур III (а) и I’ (б), квазипериодических монодисперсной (в)
и коррелированной полидисперсной I’ (г) структур
61

Квазипериодическая полидисперсная структура (рис. 1.18, г) образована внесением корреляций или «привязок» к заданной монодисперсной квазипериодической структуре. Считаем, что в поперечной плоскости изотропии над каждым круговым сечением волокна радиуса r монодисперсной квазипериодической структу-
ры мысленно расположено концентрическое круговое сечение волокна радиуса r I' некоторой составной ячейки с внешним радиу-
сом RI' полидисперсной структуры; центр каждой гексагональной
ячейки с волокном квазипериодической монодисперсной структуры совпадает с центром соответствующей составной ячейки полидисперсной структуры. Так как в заданной квазипериодической монодисперсной структуре радиусы всех волокон одинаковые и равны r , поэтому в «привязанных» к ним волокнах полидисперс-
ной структуры радиусы тоже считаем одинаковыми и равными r I' и в общем – r rI' . В полидисперсной структуре пространство
между привязанными квазипериодическими монодисперсными составными ячейками заполнено такими же по строению, но полидисперсными, например, бесконечно малыми однотипными ячейками с волокном.
Коэффициенты корреляции периодической, квазипериодической и полидисперсных структур. Определим коэффициен-
ты корреляции различных пар: квазипериодических монодисперсной (см. рис. 1.18, а) и полидисперсной (см. рис. 1.18, б), монодисперсных квазипериодической и периодической, периодических монодисперсной и полидисперсной случайных структур.
Рассмотрим расчет коэффициента корреляции p1 квазипери-
одических монодисперсной и полидисперсной структур. Коэффициент корреляции
iI'/i/
p1 = 1I' 1 (1.106)
1 1
62

случайных статистически однородных индикаторных функций 1-й фазы (волокон) двухфазных квазипериодических монодисперсной
i (r) и полидисперсной |
iI' (r) структур |
|
|
|
|||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
i (r) = |
1, |
r V |
iI' (r) = |
1, |
r VI' |
(1.107) |
|||||
0, |
|
1 |
0, |
1 |
|||||||
1 |
|
r V |
1 |
|
r VI' |
|
|||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
рассчитывается |
|
|
|
|
|
|
|
|
|
|
|
p1 |
= |
|
v11 − v12 |
, |
v11 |
= i1I'i1 |
|
(1.108) |
|||
v (1− v ) |
|
||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
через одноточечный начальный смешанный момент v11 , где пуль-
сации i1I'/ (r) = i1I' (r) − i1I' , i1/ (r) = i1 (r) − i1 |
, осредненные значения |
||||||||
iI' |
|
= v , |
среднеквадратические |
отклонения |
I' = = |
|
, |
||
= i |
D |
||||||||
1 |
1 |
1 |
|
|
|
1 |
1 |
11 |
|
дисперсия D |
(1.15), области 1-й V , |
VI' |
и 2-й V |
, VI' фаз обеих |
|||||
|
|
11 |
1 |
1 |
2 |
|
2 |
|
|
структур в представительной области |
V = V1 V2 . |
Для тривиаль- |
|||||||
ного случая, когда полидисперсная некоррелированная структура произвольным образом «накладывается» на монодисперсную ква-
зипериодическую структуру имеем v11 = v12 , p1 = 0 .
Из формулы для объемной доли волокон в монодисперсной квазипериодической структуре
v = p (r |
/ r |
)2 v |
(1.109) |
|
1 |
|
max |
1max |
|
следует, что радиус вписанной в гексагональную ячейку окружности
rmax = r |
p v1max / v1 |
. |
(1.110) |
Объемная доля волокон в монодисперсной квазипериодической структуре (1.109) равна объемной доле волокон в полидис-
персной структуре и в каждой ее составной ячейке v1 = (rI' / RI' )2 , где внутренний r I' и внешний RI' радиусы однотипной составной ячейки полидисперсной структуры. Минимальная гарантированная
63
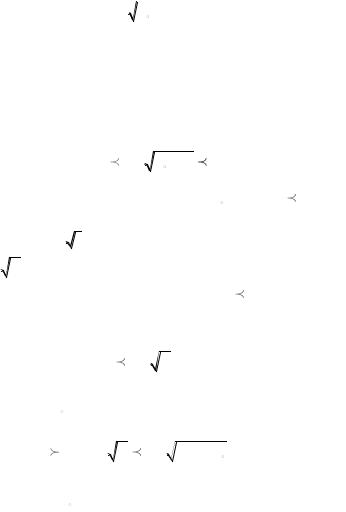
прослойка между волокнами в монодисперсной квазипериодической структуре
= 2r ( |
p v1max / v1 |
−1). |
(1.111) |
Из условия статистической независимости реализаций структуры в различных, в частности, соседних гексагональных ячейках квазипериодической структуры следует требование невыхода точек составной ячейки за границу своей привязанной гексагональной ячейки, т.е. внешний радиус соответствующей привязанной ячейки
RI' rmax :
0 x |
p v1max |
|
1 |
(1.112) |
с учетом формулы (1.110) и неравенств: |
p 1, v1max |
1, где мак- |
||
симально возможная объемная доля волокон при гексагональной
укладке |
|
|
v1max = |
3 |
/ 6 0,906, |
радиус составной |
ячейки |
||
RI' = rI' |
/ |
|
|
, отношение радиусов связанных волокон |
x = rI' / r . |
||||
v |
|||||||||
|
|
1 |
|
|
|
|
|
|
|
Из формулы (1.112) следует, что всегда rI' r при требовании
RI' rmax .
В частных случаях (1.112):
1) если RI' r |
или 0 |
x |
|
, имеем |
|
|
|||||
v |
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
v |
= p |
|
rI'2 |
+ |
(r2 − RI'2 ) v |
|
= v2 |
, |
p = 0 ; |
||
11 |
|
|
S |
|
S |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
2) если RI' |
|
или |
|
|
|
|
|
|
|
|
, |
имеем |
|
|||
r |
|
v |
|
x v |
|
/ p |
|
|||||||||
|
|
|
|
1 |
|
|
|
1max |
|
|
|
|
|
|
||
|
|
rI'2 |
+ 0 |
|
= v x2 , |
|
|
x2 |
− v |
, |
(1.113) |
|||||
v |
= p |
|
|
|
p = |
|
|
1 |
||||||||
|
|
1− v |
||||||||||||||
11 |
|
S |
|
|
|
1 |
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
где площадь гексагональной ячейки S. Решение (1.113) для одното- |
||||||||||||||||
чечного момента v11 |
и коэффициента корреляции |
p1 |
можно пред- |
|||||||||||||
ставить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

v |
= p v v |
, p = |
v1 |
, |
(1.114) |
||
1− v |
|||||||
11 |
1 |
1max |
1 |
|
|
||
|
|
|
|
1 |
|
|
|
где параметр = ' (1+ ' / 4) |
рассчитывается через заданное значе- |
||||||
ние фиксированной относительной толщины ' = / r минималь-
ной гарантированной прослойки между волокнами в монодисперсной квазипериодической структуре; в частном случае, когда = 0,
имеем p1 = 0 (1.114). При постоянстве прослойки при варьировании объемной доли волокон v1 (0;v1max ) вероятность наличия монодисперсных волокон квазипериодической структуры в узлах
гексагональной решетки изменяется p0 = v1 / v1max , |
максимальное |
||||
значение объемной доли волокон |
|
||||
|
|
|
|
|
|
v1max = |
3 |
. |
(1.115) |
||
6(1+ ' / 2)2 |
|||||
Из формулы (1.113) видно, что максимальное значение коэффициент корреляции p1 принимает при наибольшем допусти-
мом значении параметра
x = |
p v1max |
. |
(1.116) |
Например, при v1 0,65 |
и p = v1max 0,906 из |
формулы |
|
(1.116) следует, что относительный радиус привязанного волокна полидисперсной структуры x 0,906 и коэффициент корреляции
квазипериодических монодисперсной и полидисперсной связанных структур
p1 0,49. (1.117)
Отметим, что минимальная гарантированная прослойка между волокнами для квазипериодической монодисперсной структуры (1.111) в рассматриваемом случае 0,248r .
Для сравнения рассчитаем коэффициент корреляции p2 связанных монодисперсных квазипериодической ( p (0;1)) и привя-
65

занной периодической ( p =1) структур; центры и границы ячеек
обеих структур совпадают. Радиусы круговых сечений волокон для квазипериодической структуры
r = rmax |
v1 / ( p v1max ) |
(1.118) |
и для идеальной периодической структуры
|
|
(1.119) |
r p = r p |
||
с учетом формул (1.109), (1.110) и равенства объемных долей волокон v1p = v1 в обеих структурах
|
|
v = (r p )2 / |
S = p r2 / S. |
|
|
(1.120) |
|||
|
|
1 |
|
|
|
|
|
|
|
|
Далее, так как в выражении (1.119) всегда |
r p |
r , |
поэтому |
|||||
v |
= p (r p )2 |
/ S, и в результате |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
v |
= p v , |
p = |
p − v1 |
, |
|
|
(1.121) |
|
|
|
|
|
|||||
|
|
11 |
1 |
2 |
1− v1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
и для рассматриваемого случая, когда v1 0,65 и |
p = 1max |
0,906, |
|||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
p2 0,73. |
|
|
|
|
(1.122) |
|
Аналогично формулам (1.118) – (1.122) рассчитаем коэффициент корреляции p3 связанных периодических монодисперсной и
полидисперсной структур. Радиусы круговых сечений связанных волокон для периодических полидисперсной
|
rI'' |
= r |
|
|
|
(1.123) |
|
|
v |
||||
|
|
max |
1 |
|
|
|
и монодисперсной |
|
|
|
|
|
|
|
|
|
(1.124) |
|||
r p = r |
|
v / v |
||||
|
max |
1 |
1max |
|
||
структур с учетом выражений (1.109), (1.110) и равенства объемных долей волокон v1p = v1 в обеих структурах
66
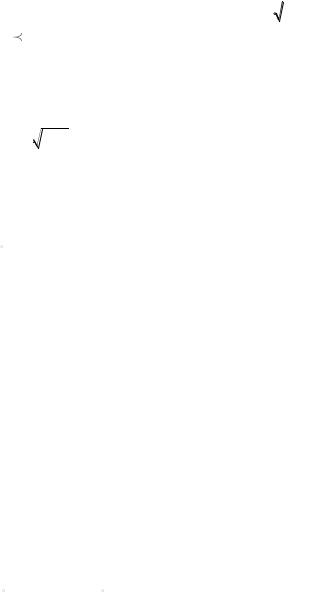
|
|
v |
|
= (r p / r |
)2 v |
|
= (rI'' |
/ r |
)2. |
|
|
|
(1.125) |
||||||
|
|
1 |
|
max |
1max |
|
|
|
max |
|
|
|
|
|
|||||
Далее, так как из (1.123), (1.124) следует rI'' = r p |
|
|
|
и не- |
|||||||||||||||
v |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1max |
|
|
равенство |
rI'' |
r p |
, |
поэтому |
v |
= (rI'' )2 |
/ S = x2 (r p )2 |
/ S, и в ре- |
|||||||||||
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
зультате |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= x2v |
, |
|
|
x2 |
− v |
, |
|
|
|
(1.126) |
|||
|
|
|
|
v |
p = |
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
11 |
1 |
|
3 |
|
1− v1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где x rI'' / r p = |
|
, |
и для |
рассматриваемого |
случая, |
|
когда |
||||||||||||
v |
|
||||||||||||||||||
|
|
|
|
1max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v1 0,65 и v1max 0,906, имеем коэффициент корреляции |
|
|
|||||||||||||||||
|
|
|
|
|
|
p3 0,73. |
|
|
|
|
|
|
|
(1.127) |
|||||
Таким |
образом, |
для |
рассматриваемого |
случая, |
|
когда |
|||||||||||||
v1 0,65, |
p = v1max |
0,906, коэффициенты корреляции связанных |
|||||||||||||||||
структур имеют значения: 0,49 для квазипериодических монодисперсной и полидисперсной (1.117), 0,73 для монодисперсных квазипериодической и периодической (1.122) и также для периодических монодисперсной и полидисперсной (1.127). Отметим, что численное значение коэффициента корреляции p 0,5 (1.102) хо-
рошо согласуется со значением 0,49, найденным из условия наилучшей полидисперсной аппроксимации корреляционной функции реальной структуры (1.117), и со значением для «приведенного коэффициента корреляции» p• = p2 p3 0,53 [55].
Двухточечная корреляционная функция квазипериодической полидисперсной структуры. Рассмотрим вычисление
нормированной двухточечной корреляционной функции k11I' (ρ) (1.67) индикаторной функции 1-й фазы i1I' (r) (1.107) для двухфаз-
ной квазипериодической полидисперсной структуры (рис. 1.18, б) в представительной области V, где вектор ρ (1.52), дисперсия D11
(1.15), начальное значение k11I' (0) =1. Считаем, что в формуле (1.67) точки: r V , r1 V , где V – область рассматриваемой составной цилиндрической ячейки с радиусом кругового поперечного сечения
67
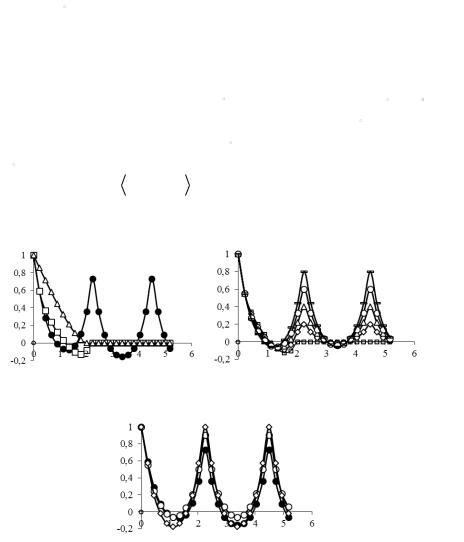
волокна r в представительной области V полидисперсной структуры. Нормированная корреляционная функция k11I' (ρ) (1.67) рас-
считывается (1.73) через условную вероятность PI' (r,r ) – вероят-
11 1
ность появления в точке r1 V 1-й фазы полидисперсной структуры при условии, что точка r V 1 находится 1-й фазе V 1 V рассматриваемой составной цилиндрической ячейки V . Так как вероятность попадания точки r V в 1-ю фазу составной ячейки V равна объемной доле v1 1-й фазы в этой ячейке, поэтому двух-
точечный момент iI' (r)iI' (r ) |
= v PI' |
(r,r ) выражается через услов- |
||||
|
1 |
1 |
1 |
1 |
11 |
1 |
ную вероятность PI' |
(r,r ) |
(1.73). |
|
|
||
11 |
|
1 |
|
|
|
|
k11 |
|
|
|
|
|
k I' |
|
|
|
|
|
|
11 |
/Rp |
/Rp |
а |
б |
k11 |
|
/Rp
в
Рис. 1.19. Нормированные корреляционные функции традиционных полидисперсных (а), квазипериодических полидисперсных (б), квазипериодических и периодической (в) структур
68

Для монодисперсных периодической и квазипериодических структур точки: r V p , r1 V , где V p – область ячейки перио-
дичности или квазипериодичности этих структур. На рис. 1.19 представлены результаты расчета нормированных корреляционных
функций k11(ρ) различных структур при объемной доле волокон v1 = 0,65, расстояние ρ = ρ (1.52), (1.68) между точками r и r1 . На рис. 1.19, а, изображены графики функций k11(ρ) для традицион-
ных полидисперсных структур: (□) для структуры на рис. 1.18, а,
(Δ) для структуры на рис. 1.18, б, с отсутствием корреляций размеров и типов ячеек в каждой из этих структур; в сравнении с кривыми (□), (Δ) на рис. 1.19, а, приведен график нормированной корреляционной функции (●) для заданной квазипериодической монодисперсной структуры (рис. 1.18, в) при значении величины
минимальной относительной толщины прослойки ' 0,25 между волокнами (1.111), ' 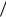 Rp . На рис. 1.19, б – графики k11I' (ρ) для
Rp . На рис. 1.19, б – графики k11I' (ρ) для
квазипериодических полидисперсных структур при различных значениях вероятности расположения монодисперсных волокон в уз-
лах гексагональной решетки: p0 = 0 (□); 0,2 (◊); 0,4 (Δ); 0,6 (○); 0,8 ( ); в предельном случае, когда p0 = 0, такая квазипериодическая
); в предельном случае, когда p0 = 0, такая квазипериодическая
структура вырождается в традиционную некоррелированную полидисперсную структуру (см. рис. 1.18, а; (□) рис. 1.19, а). На рис. 1.19,
в – графики k11(ρ) для коррелированных квазипериодических мо-
нодисперсной |
(●) |
(рис. 1.18, |
в), |
полидисперсной |
(○) |
( k11I' (ρ) ) (рис. 1.18, г) структур и, дополнительно, монодисперсной периодической структуры с гексагональной укладкой волокон (◊). Отметим наличие периодичности у «хвостов» функций k11(ρ) для
квазипериодических (см. рис. 1.18, в, г) и периодической структур, обусловленной периодичностью в расположении узлов гексагональной решетки.
69
Глава 2. ПОСТАНОВКА И МЕТОДЫ РЕШЕНИЯ СТОХАСТИЧЕСКОЙ СВЯЗАННОЙ КРАЕВОЙ ЗАДАЧИ МАГНИТОЭЛЕКТРОУПРУГОСТИ
Прогнозирование эффективных физико-механических свойств структурно-неоднородных, в том числе пьезоактивных [9; 19; 34; 76; 102], сред является одной из центральных задач механики композитов. В частности, на основе решения задачи протекания для микронеоднородной области могут быть определены эффективные, например диэлектрические, проницаемости композита [2; 9; 25; 102; 104]. Без учета пьезоактивности фаз известны различные решения [9; 104] для эффективных диэлектрических проницаемостей композита, наиболее известные из которых – это решения Фойгта – Рейсса, Хашина – Штрикмана и Максвелла – Гарнета.
Решения Фойгта
λ*F = λ |
(2.1) |
и Рейсса
λ*R−1 = 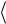 λ−1
λ−1
образуют вариационную «вилку», внутри которой лежат действительные λ* значения диэлектрических проницаемостей композита
λ*R λ* λ*F . |
(2.2) |
Решения, или вилка Хашина – Штрикмана λ*(1) , λ*(2) [9, 104] лежат внутри границ решения Фойгта – Рейсса (2.2)
λ*R λ*(1) λ* λ*(2) λ*F .
Для однонаправленного двухфазного волокнистого композита тензоры λ*(1) , λ*(2) могут быть получены [104] из решения задачи
о нагружении продольным или поперечным электрическим полем составного цилиндра полидисперсных моделей, представленных на
70
