Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Пьезокомпозиты и датчики в 3 ч. Ч. 1 Статистическая механика пьезокомпозитов

.pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

4.82 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 243 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

по областям V (1.6) и f-й фазе Vf композита.

Для двухфазных (F = 2) структур композитов взаимное рас-

положение включений (1-й фазы), например в квазипериодической и периодической структурах, задаем через соответствующие индикаторные функции

i	1,	r V		1,	r V p	,		(1.11)
i	(r) =	1	,...i p (r) =		1	,		(1.11)
1	0,	r V	1	0,	r V p
		2			2
для точек r V представительной области V = V						V = V p		V p ,
					1	2	1	2

где V1,V1p и V2 ,V2p – области 1-й и 2-й фаз обеих структур, верхний

индекс «р» обозначает принадлежность к идеальной периодической структуре. Отметим, что индикаторные функции 2-й фазы одноточечные начальные

	in		= v					(1.12)
	1			1
и центральные
/n	= v1(1− v1)			− v1)	n−1	− (−v1)	n−1	(1.13)
i1	= v1(1− v1)	(1		− v1)		− (−v1)		(1.13)

моменты n-го порядка (n = 1, 2, …) для индикаторной функции i1(r) (1.7) 1-й фазы двухфазной случайной, например квазипериодической структуры, рассчитываются через величину относительного

объемного содержания 1-й фазы v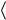1 = i1 в объеме композита, где пульсация

i/ (r) = i (r) − v .			(1.14)
1	1	1

Одноточечные моменты в формулах (1.12), (1.13) не учитывают взаимного расположения фаз и совпадают для различных случайных структур при одинаковой объемной доле фаз. В частности, центральные моменты 2-го порядка или дисперсии для квазипериодической и периодической структур

D	= i/2	= v (1− v ),		D p	i p/2	= v p (1− v p ) ,		(1.15)
11	1	1	1	11	1	1	1

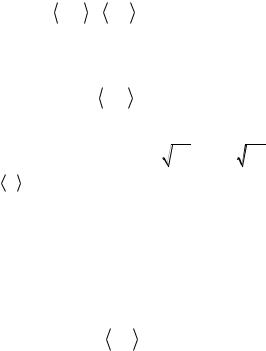
будут равны D11 = D11p при равенстве v1 = v1p , где для периодичекой структуры объемная доля v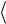1p = i1p , пульсация i1p/ (r) = i1p (r) − v1p .

Взаимное расположение включений, например в квазипериодической структуре, в неполной мере характеризует одноточечный смешанный корреляционный момент

i/i p/	= i i p		− v2	,	(1.16)
1 1	1	1	1

коэффициент корреляции или «коэффициент периодичности» [32] p (0;1) квазипериодической и периодической структур

					i/i p /
		p =			1 1		,					(1.17)
		p =					,					(1.17)
						p
					1	1
где среднеквадратичные отклонения =										, p		, опера-
где среднеквадратичные отклонения =									D	, p	= D p	, опера-
							1		11	1	11
тор осреднения ...	(1.6). Для квазипериодических структур вы-
полняется равенство	v	= v p ,	и		формула				расчета		коэффициента
	1	1
корреляции (1.17) имеет вид
				v − v2				,				(1.18)
		p			11	1
		p	v		(1− v )
			v		(1− v )
				1		1
где корреляционный момент
		v		= i i p .								(1.19)
		11			1	1

Геометрический смысл величины v11 – это относительное

объемное содержание области пересечения включений при мысленном наложении квазипериодической структуры на идеальную периодическую структуру.

Отметим, что для квазипериодической структуры со случайными независимыми для каждой ячейки отклонениями a центров, например круговых или сферических включений 1-й фазы из узлов идеальной периодической решетки, выполняется равенство

i (r) = i p (r −a)		(1.20)
1	1
между индикаторными функциями i (r) и		i p (r) для каждой ячейки
	1	1

квазипериодической структуры.

Свойства пульсаций и корреляционных моментов двух-

фазных структур. Рассмотрим формулировку и доказательство свойств смешанных центральных одноточечных моментов случай-

ных индикаторных функций i (r)				и i p	(r) однородных включений;
			1	1
пульсации обозначим
i/ (r) = i (r) − v ,				i/ p (r) = i p (r) − v .			(1.21)
1	1		1	1	1	1
Лемма 1.1. Выполняется разложение
		i/k = i/k		+	i/		(1.22)
		1	1		(k ) 1
для пульсаций индикаторной функции i/ , где						k =1, 2,..., разность
					1
		(k )	(1− v )k − (−v )k				(1.23)
		(k )		1	1

вычисляется через величину v1 относительного объемного содержания включений в композите.

Доказательство. Пульсации индикаторной функции i1/ в k-й степени возможно представить через разложение

i/k = i (1− v )k + (1−i )(−v )k
1	1	1	1		1
или в виде
	i/k	= (−v )k +		i		(1.24)
	1	1	(k ) 1
с учетом обозначения (k ) (1.23). Осредним оператором						... урав-
нение (1.24)
	i/k	= (−v )k +		(k )	v .	(1.25)
	1	1		(k )	1

Вычтем уравнение (1.25) из (1.24) и в результате получим формулу

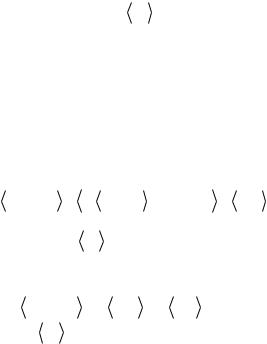
i/k − i/k		=	i/ ,	(1.26)
1	1		(k ) 1

подтверждающую формулу (1.22). Доказательство закончено. Лемма 1.2. Отношение смешанного центрального момента

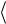i1/ (i1/ p )n−1 к центральному моменту 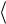i1/ n есть величина, не зави-

сящая от порядка n = 2, 3, … (1.17) – (1.19).

Доказательство. С учетом формул (1.22), (1.23) центральные моменты 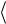i1/ (i1/ p )n−1 , 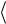i1/ n представим в виде

i/ (i/ p )n−1	= i/ [	(i/ p )n−1	+		i/ p		]	= i/i/ p	(n−1)	, (1.27)
1 1	1	1		(n−1) 1				1 1	(n−1)
	i/n	= v (1− v )			(n−1)	.				(1.28)
	1	1	1		(n−1)

Таким образом, отношение центральных моментов

i/ (i/ p )n−1			i/i/ p		i i p	− v2
1 1	=		1 1	=	1 1	1	p	(1.29)
i/n	=	v	(1− v )	=	v (1− v )		p	(1.29)
i/n		v	(1− v )		v (1− v )
1	1		1		1	1

равно коэффициенту корреляции (периодичности) p (1.18) с уче-

том формулы (1.19). Доказательство закончено.

Коэффициент периодичности p [0;1] при фиксированном значении относительного объемного содержания включений v1 есть функция от характеристики упорядоченности v11 (1.19). В предельных случаях имеем p =1 и v11 = v1 , когда квазипериодическая структура тождественна периодической, и p = 0 и v11 = v12 ,

например, когда квазипериодическая структура вырождается в структуру типа «статистическая смесь», у которой полностью отсутствует корреляция физико-механических свойств в различных точках среды. Задача вычисления коэффициента периодичности p

сведена к расчету характеристики упорядоченности v11 (1.19) в

формуле (1.18). Рассмотрим вычисление коэффициентов периодичности p для различных квазипериодических структур.

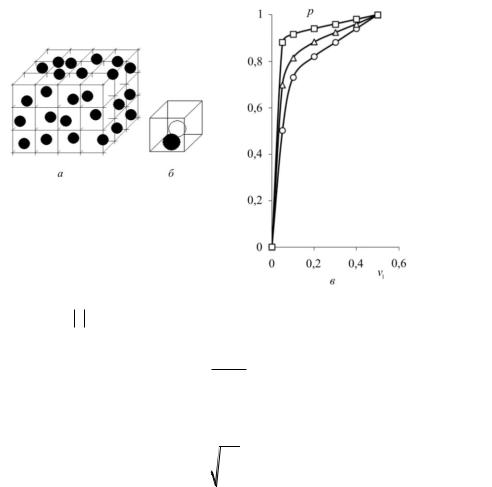
Сферокомпозит. Пусть квазипериодическая структура сферокомпозита (рис. 1.3) образована независимыми для каждой ячейки случайными отклонениями a центров сферических включений

детерминированного радиуса r от узлов правильной решетки с

ячейкой периодичности в виде куба. Свойство квазипериодичности структуры и независимость случайных отклонений a для различных ячеек позволяет перейти к рассмотрению одиночной ячейки квазипериодичности на рис. 1.3, б. Все ориентации случайного вектора смещений a равновероятны, и его модуль a распределен по

равномерному закону на отрезке [0; ], где = k max , k [0;1] – степень разупорядоченности сферических включений, параметр ячейки max = T / 2 − r – предельный радиус сферы, выход за кото-

рую центра включения считаем невозможным, так как это приводит к выходу включения за границу ячейки, где период или ребро

T = r 34 / (3v1 ) кубической ячейки.

Таким образом, расчет величины характеристики упорядоченности v11 (1.19) сводится к задаче осреднения

		mv
v11	=	mv	,	mv	= V11(x) f (x)dx	(1.30)
v11	=	3	,	mv	= V11(x) f (x)dx	(1.30)
		T			−
для заданной функции плотности вероятностей f (x)						равномерного
распределения
	f (x) =			1/ t,	x [0;t]	(1.31)
	f (x) =				x [0;t]	(1.31)
				0,	x [0;t]

удвоенного объема шарового сегмента

		3
V11		2 r	(1− x)2 (2 + x),	0 x 1,	(1.32)
V11	(x) =	3			(1.32)
			0,	x 1,
			0,	x 1,

где
x	a	(1.33)
x	2r	(1.33)
	2r

Рис. 1.3. Сферокомпозит (а)

сячейкой квазипериодичности (б)

икоэффициент периодичности p (в)

для степени разупорядоченности k =1 (○), 2/3 (Δ), 1/3 (□)

модуль a = a вектора отклонений a , нормированный параметр

t	k max	(1.34)
	2r

для рассматриваемой квазипериодической структуры равен


	k		4
t =		3		− 2	.	(1.35)
t =	4	3	3v	− 2	.	(1.35)
	4		3v
			1

В результате для расчета величины характеристики упорядоченности v11 сферокомпозита с квазипериодической структурой может быть получена формула

			3v1	,	0 v		c ,
			3v1	,	0 v		c ,
			8t			1	1
v11			8t				(1.36)
v11	=	v1					(1.36)
		v1	[3 + (1− t)4	− 4(1− t)3 ],	c	v	v ,
			[3 + (1− t)4	− 4(1− t)3 ],	c	v	v ,
		8t			1	1	max
		8t

где предельно допустимое значение относительного объемного содержания сферических включений в композите

					vmax = / 6,					(1.37)
					k3
структурный параметр c1			=				.
структурный параметр c1			=	6(2 + k)3			.
Таким образом, коэффициент периодичности p сферокомпо-
зита с квазипериодической структурой имеет вид
			3		− v
			8t		− v
			8t	1		,			0 v1	c1 ,
				1

			1	− v1
			1	− v1						(1.38)
p =	1	[3 + (1− t)4 − 4(1− t)3 ] − v								(1.38)
	1

	8t					1		,		vmax .
	8t								c1 v1
			1	− v1					c1 v1
			1	− v1

На рис. 1.3, в, представлены результаты расчета коэффициента периодичности p сферокомпозита для разных значений степени

разупорядоченности k и в зависимости от величины относительного объемного содержания v1 сферических включений.

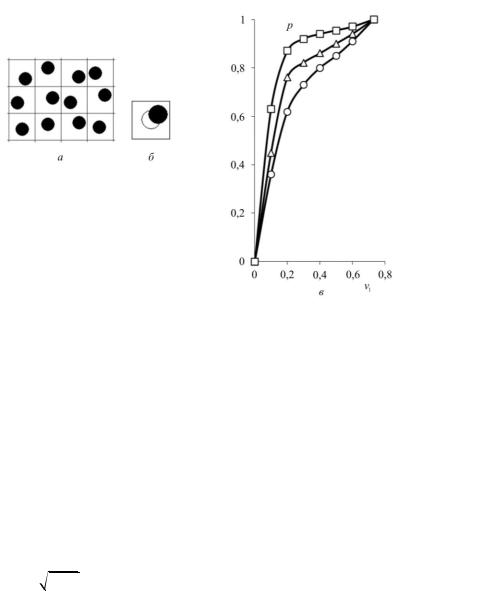
Рис. 1.4. Волокнистый композит (а)

сячейкой квазипериодичности (б)

икоэффициент периодичности p (в) для степени

разупорядоченности k =1 (○), 2/3 (Δ), 1/3 (□)

Однонаправленный волокнистый композит. Для расчета коэффициента периодичности p однонаправленного волокнистого

композита (рис. 1.4, а), квазипериодическая структура которого образована независимыми для каждой ячейки случайными отклонениями a от узлов правильной квадратной решетки в плоскости

r1r2 , ориентированных вдоль оси r3 волокон с детерминированным радиусом r поперечных круговых сечений, достаточно рассмот-

реть плоскую модель ячейки квазипериодичности «круг в квадрате». В этой модели случайные ориентационный угол и модуль a

вектора отклонений a распределены по равномерным законам на отрезках [0; 2 ] и [0; ] соответственно, где = k max , степень разупорядоченности волокон k [0;1], величина максимально допустимого смещения max = T / 2 − r , период или сторона T = r / v1 квадратной ячейки.

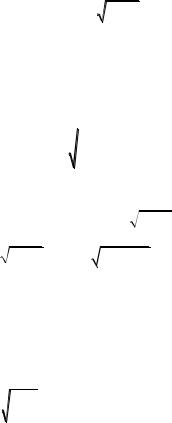
Таким образом, определение величины характеристики упорядоченности v11 сводится к задаче осреднения

		ms
v11	=	ms	,	ms = S11(x) f (x)dx	(1.39)
v11	=	2	,	ms = S11(x) f (x)dx	(1.39)
		T		−
				−
для заданной функции плотности вероятностей f (x)					равномерного

распределения (1.31) удвоенной площади кругового сегмента

S (x) =		2	(arccos(x) − x 1− x	2	),
S (x) =	2r		(arccos(x) − x 1− x		),
11			0,

	0 x 1,	(1.40)
	x 1,	(1.40)
	x 1,

где параметр x связан с величиной модуля a вектора отклонений зависимостью (1.33), нормированный параметр t для рассматриваемой квазипериодической структуры равен



	k			(1.41)
t =			− 2 .
t =	4		− 2 .
	4	v
		1

Вспомогательные выражения для неопределенных интегралов:

arccos(x)dx = x arccos(x) − 1− x2 ,

x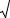1− x2 dx = − 13 (1− x2 )3 .

Врезультате для расчета коэффициента периодичности p может быть получена формула

− v

3 t

0 v1

c1 ,

− v1

(1.42)

p =

3/2

(1− t

)

−1

arccos(t) + t −

−1 +

− v1

, c1

vmax ,

− v1

или, используя переменную = arccos(t) , получим

−

0 v c ,

3 cos (1− v1 )

1− v1

2 − 3sin

+ sin

(1.43)

p =

3cos

−

c1 v1

vmax ,

(1− v1 )

1− v1

где предельно допустимое значение относительного объемного содержания волокон в композите

vmax = / 4,

(1.44)

структурный параметр c1 = k 2 2 . 4(2 + k)

На рис. 1.4, в, и дополнительно на рис. 1.5, в, представлены результаты расчета коэффициента периодичности p однонаправленного волокнистого композита для разных значений степени разупорядоченности k и в зависимости от величины относительно-

го объемного содержания v1 волокон. Квазипериодическая струк-

тура на рис. 1.5, б, образована статистически однородным случайным размещением центров поперечных сечений однонаправленных волокон в узлах идеальной гексагональной решетки с учетом заданных значений относительного объемного содержания волокон

v1 и минимальной гарантированной прослойки матрицы между ними в 5 % от радиуса волокна r .

Таким образом, при фиксированном значении v1 увеличение степени разупорядоченности k приводит к уменьшению как v11 , так и p. Когда v1 → vmax , тогда разупорядоченность, например, сфе-

рических включений (см. формулу (1.37)) или волокон (см. формулу (1.44)), из-за уплотнения укладки становится невозможной, и коэффициент периодичности p →1.

<<< < Предыдущая 1 23 / 243 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в папке книги

#
12.11.20231.57 Mб2Психология делового общения..pdf
#
12.11.20233.67 Mб1Психология личности..pdf
#
12.11.202311.12 Mб31Психология перевода как сложного вида иноязычной речевой деятельности..pdf
#
20.11.2023512.8 Кб0Публичный отчёт Научной библиотеки Пермского национального исследовательского политехнического университета.-1.pdf
#
12.11.20231.37 Mб1Пути сохранения личностного потенциала пожилого человека..pdf
#
12.11.20234.82 Mб6Пьезокомпозиты и датчики в 3 ч. Ч. 1 Статистическая механика пьезокомпозитов.pdf
#
12.11.20234.17 Mб0Работа с базой данных ProQuest Dissertations & Theses Global..pdf
#
12.11.20233.82 Mб1Работа с ресурсами портала гуманитарного факультета рекомендации по созданию электронного курса..pdf
#
12.11.20231.84 Mб4Работа с электронным тахеометром GTS-105N..pdf
#
12.11.20231.4 Mб3Работа с электронными таблицами EXCEL..pdf
#
12.11.20236.76 Mб1Работы по термодинамике и кинетике химических процессов..pdf