
книги / Пьезокомпозиты и датчики в 3 ч. Ч. 1 Статистическая механика пьезокомпозитов
.pdf
a(3,3) |
= − |
+ s |
h |
+ (1− 2v ) |
|
|
|
|
− (2)s |
+ (1− 2v ) |
; |
|||||||||||||||||||||||||||||||||||||||||||
h |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ik |
ik |
idb kdb |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
kdb |
|
|
|
|
|
|
id |
|
|
|
|
dk |
|
1 |
dk |
|||||||||||||||||||
правые части для 1-й системы уравнений (2.117) |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b(1) |
=U s |
|
|
|
|
|
|
|
|
|
|
|
+U (1)s e |
|
|
|
+U (2)s |
|
|
|
|
|
|
, |
|
|||||||||||||||||||||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
h |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
ijmn |
|
(ij)ks ksmn |
|
|
|
|
|
|
|
|
(ij)k kmn |
|
|
|
|
|
|
|
(ij)k kmn |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
+ ik(1)s ekmn |
+ (2)ik |
s |
|
kmn , |
|
|
(2.122) |
||||||||||||||||||||||||||||||||||||||||
|
|
bimn(2) = ikss C |
ksmn |
h |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ksmn + ik(1)s ekmn |
|
+ ik(2)s |
|
|
|
|
kmn , |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
bimn(3) = ikss C |
|
h |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
для 2-й и 3-й систем уравнений (2.118), (2.119): |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
c(1) |
= −U s |
|
|
|
e |
|
|
+U |
(1)s |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
kn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
ijn |
|
|
|
|
|
|
|
(ij )ks nks |
|
|
(ij)k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
cin(2) = −ikss |
|
|
|
|
|
|
+ ik(1)s |
|
kn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.123) |
|||||||||||||||||||||||||
|
|
|
enks |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
cin(3) |
|
= −ikss enks |
+ ik(1)s |
|
kn , |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
d (1) |
= −U s |
|
|
|
|
|
|
|
|
|
|
(2)s |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
h |
|
|
+U |
kn |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
ijn |
|
|
|
|
|
|
|
|
(ij)ks nks |
|
|
(ij)k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
din(2) |
|
|
|
|
|
|
|
|
+ ik(2)s kn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.124) |
|||||||||||||||||||||||||||
|
|
|
= −ikss |
h |
nks |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
din(3) |
|
|
|
|
|
|
|
+ ik(2)s kn , |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= −ikss |
h |
nks |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
и для 4-й системы уравнений (2.120) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
f (1) |
= −U s |
|
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
(2)s |
|
|
|
|
, |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
+U |
|
|
|
|
+U |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
ij |
|
|
|
|
(ij)ks ks |
|
|
|
|
|
|
|
|
(ij)k |
|
k |
|
|
|
|
|
|
|
|
(ij)k k |
|
|
|
||||||||||||||||||||||||
|
|
|
(2) |
|
|
|
|
|
+ ik(1)s k |
+ ik(2)s |
|
|
k , |
|
|
(2.125) |
||||||||||||||||||||||||||||||||||||||
|
|
fi |
= −ikss |
ks |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(3) |
= −ikss |
|
|
|
+ ik(1)s k |
|
+ ik(2)s |
|
k . |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
fi |
ks |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
В формулах (2.121) – (2.125) индексы в круглых скобках (ij)
обозначают выделение симметричной составляющей по этой паре индексов.
Сингулярные составляющие вторых производных функ-
ций Грина для пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности. В формулах (2.121) – (2.125) компо-
ненты матрицы Gs (2.115) тензоров сингулярных составляющих
121
вторых производных для функций Грина G (2.106), (2.114) вычисляются по формулам
Uimjns |
|
|
|
|
|
ij ]mn , |
Uimn(1)s |
|
|
|
|
i(1) ]mn , |
|
|
|
|
i(2) ]mn ; |
|
||||
=[U |
=[U |
Uimn(2)s =[U |
|
|||||||||||||||||||
mjns |
=[ |
|
|
j ]mn , |
(1)mns =[ |
|
|
(1) ]mn , |
(2)mn s =[ |
|
|
|
(2) ]mn ; |
(2.126) |
||||||||
|
|
|
||||||||||||||||||||
mjns |
=[ |
|
j ]mn , |
(1)mns |
=[ |
|
(1) ]mn , |
(2)mn s =[ |
|
(2) ]mn , |
|
|||||||||||
|
|
|
|
|||||||||||||||||||
где оператор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
(2.127) |
|||||
|
|
|
[...]mn = − |
... m n sin d d |
||||||||||||||||||
|
|
|
4 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действует на компоненты тензоров
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(1)h(1) |
|
|
h(2)h(2) |
|
−1 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
Uij = |
ij + |
|
|
i |
|
|
|
j |
+ |
|
|
i |
|
|
|
j |
|
|
, |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
U |
i(1) =Uij |
|
|
|
j |
|
|
, |
U |
i(2) =U |
|
|
|
|
j |
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
(1) |
|
|
ij |
|
(2) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(1) |
|
|
|
|
ij , |
|
|
|
|
|
|
|
|
|
|
|
h(2) |
|
|
|
|
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
Uij |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
j |
= |
|
|
|
|
j |
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(1) |
|
|
|
(2) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
i(1) |
−1) |
|
|
, |
|
|
|
|
|
|
|
i(1) |
, |
||||||||||||||||||||||||||||||
|
|
|
|
(1) = (hi(1)U |
|
|
|
|
(1) = hi(2)U |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(1) |
|
|
|
(2) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
i(2) |
|
1 |
|
|
, |
|
|
|
(2) |
|
|
i(2) |
−1) |
|
1 |
, |
|
|||||||||||||||||||||||||||||||
|
|
(2) = hi(1)U |
|
|
|
|
|
= (hi(2)U |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
(1) |
|
|
|
|
|
|
|
|
(2) |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(2.128)
(2.129)
в которых использованы обозначения
|
|
|
|
ij |
= Cimjn• m n , |
|
|
|
|
|
|
||||
|
|
hi(1) |
= emin• m n , |
hi(2) |
= hmin• |
m n , |
|
(2.130) |
|||||||
|
|
(1) |
= •mn m n , |
(2) |
= •mn m n , |
|
|
||||||||
= |
1 |
sin cos |
, |
|
= |
1 |
sin sin , |
|
|
= |
1 |
cos , |
(2.131) |
||
1 |
a1 |
|
2 |
|
a2 |
|
|
|
3 |
|
a3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
122

где и – полярные углы в сферической системе координат, по-
верхность эллипсоидального «зерна неоднородности» [104] задана равенством
|
3 |
|
|
|
|
|
||
|
|
|
(xi / ai )2 =1 |
(2.132) |
||||
|
|
|
i=1 |
|
||||
через |
значения главных полуосей ai в (2.131), |
координаты |
||||||
xi = r(1)i |
− ri вектора x . |
|
||||||
Тензор |
|
в формуле (2.128) является симметричным |
||||||
U |
||||||||
|
|
|
|
|
|
|
|
(2.133) |
|
|
|
Uij =U ji |
|||||
сучетом симметрии ij = ji тензора Λ . Действительно, в (2.128) компоненты
ji = C•jmin m n = C•jnim m n = Cimjn• m n ij
сучетом выражения (2.130) для компонент тензора Λ и известного
свойства симметрии C•jnim = Cimjn• к перестановке первой и второй
пар индексов тензора упругих свойств C• среды сравнения. Таким образом, благодаря свойству симметрии (2.133) для U
по индексам (ij) и симметрии оператора[...]mn (2.127) по индексам
(mn) компоненты Uimjns |
в (2.126) будут обладать симметрией по |
|||||||||||
индексам внутри пар (ij) и (mn) |
|
|
|
|
|
|
||||||
U s |
|
=U s |
=U s |
=U s |
||||||||
imjn |
|
|
injm |
|
|
jmin |
|
|
jnim |
|||
и в (2.129) будут выполняться равенства |
||||||||||||
|
i(1) |
|
|
i , |
|
|
i(2) |
|
|
|
||
U |
= |
|
U |
= i . |
||||||||
Отметим симметрию по индексам (mn) всех компонент мат-
рицы Gs (2.115) благодаря симметрии по этой паре индексов опе-
ратора (2.127).
Эффективные свойства композита. Тензоры эффективных упругих свойств C* , диэлектрической λ* и магнитной μ* прони-
123

цаемостей, пьезомеханических свойств e* и h* , коэффициентов электромагнитной связанности χ* , κ* и температурных напряжений β* , вектора эффективных пироэлектрических π* и пиромагнитных * постоянных композита, входящие в определяющие соотношения на макроуровне (2.17), могут быть вычислены по формулам
|
|
|
C* = C + |
c , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
λ* = λ + , |
|
|
|
|
μ* = μ + , |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
e* = e + |
|
|
e , |
|
|
|
|
h* = h + h , |
|
|
|
|
|
|
(2.134) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
χ* = |
|
|
|
, |
|
|
|
|
κ* = |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
β* = β + , |
|
|
|
|
π* = π + , |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
* = + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
через поправки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2)s ) |
, |
||||||
|
= v (1− v )(C |
|
|
|
|
|
A |
|
|
|
|
|
|
|
− e |
pij |
F |
|
|
|
− h |
pij |
F |
|||||||||||||||||||||||||||||||||||||||||||
ijmn |
|
1 |
1 |
|
|
ijdb dbmn |
|
|
|
|
|
|
|
|
|
|
pmn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pmn |
|
||||||||||||||||||||||||||||||||
|
|
|
= v (1− v )( |
|
|
|
|
|
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
) |
|
, |
|
|
|
|
|
||||||||||||||||||||
|
|
|
kp |
H |
+ e |
|
B |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
kn |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
kpq |
|
|
|
|
|
|
pqn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
= v (1− v )( |
|
|
|
|
|
|
|
|
(2)s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
), |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
kp |
M |
|
|
+ h |
|
|
|
D |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
kn |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
kpq |
|
|
|
|
|
|
|
|
|
pqn |
|
|
|
|
|
|
|
|
|
|
|||||||||||
e |
= v (1− v )(e |
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s ), |
|
||||||||||||||||||||||||
pij |
H |
|
+ h |
pij |
H |
|
(2)s −C |
|
|
|
|
|
B |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
nij |
|
1 |
1 |
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
|
|
ijpq |
|
|
|
pqn |
|
|||||||||||||||||||||
h |
|
= v (1− v )(e |
|
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
), (2.135) |
|||||||||||||||||||||||||||
|
pij |
M |
+ h |
pij |
M |
|
(2)s −C |
|
|
|
|
D |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
nij |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ijpq |
|
|
pqn |
|
||||||||||||||
|
|
|
= v (1− v )( |
|
|
|
|
|
|
|
|
(1)s |
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
) |
, |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
kp |
M |
+ e |
|
D |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
kn |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
kpq |
|
|
|
|
|
|
|
|
pqn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
= v (1− v )( |
|
|
|
|
|
(2)s |
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
) |
, |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
kp |
|
H |
|
+ h |
|
B |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
kn |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pn |
|
|
|
|
|
|
|
|
|
kpq |
|
|
|
|
|
|
|
|
pqn |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)s + |
|
|
|
|
|
|
|
|
(2)s ) , |
|
|||||||||||||||||||||||||||||||||||||||||
= v (1− v )(−C |
|
|
|
|
|
|
s |
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
T |
|
+ e |
|
T |
pij |
T |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ij |
|
1 |
1 |
|
|
|
|
ijdb |
db |
|
|
|
|
|
|
|
|
|
pij |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
||||||||||||||||||||||||||||
i = v1(1− v1)( ipTp(1)s + eipqTpqs ) , i = v1(1− v1)( ipTp(2)s + hipqTpqs )
к соответствующим осредненным по объему значениям C , …,
(2.134).
Композит PVDF/феррит с эллипсоидальными включени-
ями (сингулярное приближение). Проведем расчет эффективных
124
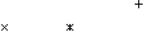
коэффициентов электромагнитной связанности трансверсальноизотропного пьезоэлектромагнитного композита: пьезоэлектрическая матрица PVDF с ориентированными эллипсоидальными ферритовыми (2.11) – (2.13) включениями (2.132) в сингулярном при-
ближении (2.134), (2.135) со |
средой сравнения (2.107)–(2.109): |
C• = C , e• = e , h• = h , |
λ• = λ , μ• = μ в сравнении с |
точным аналитическим решением для слоистого композита.
На рис. 2.4 приведены эффективные, отличные от нуля коэффициенты электромагнитной связанности 11* , *33 и 12* пьезо-
электромагнитного композита с ориентированными пьезомагнитными эллипсоидальными включениями в пьезоэлектрической матрице в зависимости от относительного объемного содержания включений v1 . Использованы следующие обозначения: □ – слои
( q → 0 ); диски: ▬ (q = 0,2), |
(q = 0,5); ○ – шары (q = 1); иглы: |
||
(q = 2), (q = 5), |
(q = 10); ◊ – волокна ( q → ) для различных |
||
геометрических |
форм эллипсоидальных включений; |
параметр |
|
q = a3 / a1(2) при |
a1 = a2 , где |
ai – главные полуоси |
включений |
(2.132). На рис.2.4 приведены результаты точного аналитического решения для слоистых структур (□), совпадающего с решением рассматриваемого сингулярного приближения при переходе к пределу a1(2) → , a3 =1 ( q → 0 ). Решения для слоистого композита и
композитов с однонаправленными волокнами и шаровыми включениями выделены полужирными кривыми. Отметим выполнение
равенств 11* = 11* , 12* = −*21 = −12* = *21 , *33 = *33 и дополнительно
*22 = 11* , *22 = 11* для ненулевых компонент тензоров χ* , κ* эффективной электромагнитной связанности (см. (2.8)).
Подтверждено, что все полученные в разделе 2.4 решения
(2.71), (2.81), (2.83), (2.85) для эффективных констант: k12* , C3333* ,
C1133* , e333* , e311* , h311* , h333* , 11* , *33 , 11* , *33 , 11* , *33 , 11* , *33 одно-
направленного волокнистого композита с полидисперсной структурой (см. рис. 1.1, б, в) в точности совпали с соответствующими
125
решениями (2.134) обобщенного сингулярного приближения, в котором свойства среды сравнения приравнены к свойствам одной из фаз (матрицы) композита.
v1 |
v1 |
|
|
* |
,нс/м |
* |
,нс/м |
11 |
|
33 |
|
|
а |
б |
|
v1
12* ,нс/м
в
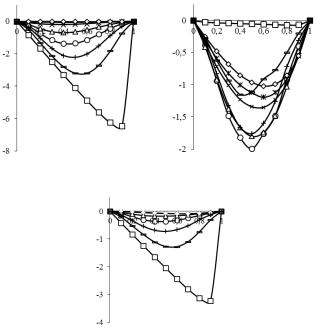
Рис. 2.4. Эффективные коэффициенты электромагнитной связанности 11* (а), *33 (б) и 12* (в) пьезоэлектромагнетика
Обобщенное сингулярное приближение. Волокнистый композит PVDF/феррит. На рис. 2.5 представлены результаты расчета [45] эффективных коэффициентов электромагнитной свя-
занности 11* , *33 и 12* (2.134) трансверсально-изотропного волок-
нистого пьезоэлектромагнетика: пьезоэлектрическая матрица PVDF с однонаправленными вдоль оси r3 ферритовыми волокнами ( a1 = a2 , a3 → (2.132)) с объемной долей v1 . Расчет (см. рис. 2.5)
проведен в обобщенном сингулярном приближении (2.114), (2.134) для четырех различных случаев выбора свойств среды сравнения
126
(2.107)–(2.109): в первом случае (Δ), ее свойства приравнены свойствам 1-й фазы (волокнам)
C• = C |
, e• = e |
, h• = h |
, λ• = λ |
1 |
, μ• = μ , |
(2.136) |
1 |
1 |
1 |
|
1 |
|
во втором случае (□) – свойствам 2-й фазы (матрице)
C• = C |
2 |
, e• = e |
2 |
, h• = h |
2 |
, λ• = λ |
2 |
, μ• = μ |
2 |
(2.137) |
|
|
|
|
|
|
в третьем случае (○) – осредненным по области V композита значениям
C• = C , e• = e , h• = h , λ• = λ , μ• = μ , (2.138)
и в четвертом случае (◊) – искомым эффективным свойствам композита (схема самосогласования)
C• = C* , e• = e* , h• = h* , λ• = λ* , μ• = μ* |
(2.139) |
решения (○), (◊) инвариантны к инверсии свойств фаз.
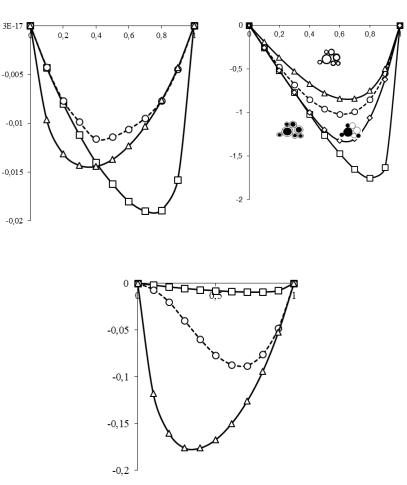
Результаты расчета (□) и (Δ) для эффективных констант 11* ,*33 (см. рис. 2.5, а, б) в обобщенном сингулярном приближении в
точности совпали с аналитическими решениями (2.66), (2.71) для полидисперсных структур на рис. 1.1, б (см. рис. 2.5, а') и рис. 1.1, в (см. рис. 2.5, б'); решение (◊) по схеме самосогласования
(см. рис. 2.2, б, для случая v0 →1 ) для *33 в точности совпало с
аналитическим решением (2.71), (2.104) для полидисперсной структуры на рис. 1.1, г (см. рис. 2.5, в'). Решения (○), (◊) при «малых» степенях наполнения v1 близки к решению (□) для матричной
по 2-й фазе структуре (см. рис. 2.5, а') и при «больших» v1 – к решению (Δ) для матричной по 1-й фазе структуре (см. рис. 2.5, б'). Отметим, что решение *33 (Δ) также в точности совпало с реше-
нием (2.85) асимптотического метода осреднения [11] для идеальной периодической волокнистой структуры.
127
v1 |
v1 |
в
а б
*33 ,нс/м
11* ,нс/м
а |
б |
v1
12* ,нс/м
в
Рис. 2.5. Эффективные коэффициенты электромагнитной связанности 11* (а), *33 (б) и 12* (в) волокнистого пьезоэлектромагнетика с объемной долей феррита v1
128
12
|
|
|
|
* |
E* / E |
E* / E |
12 |
||
|
||||
1 |
(2)1 |
3 |
(2)3 |
* |
|
|
|
|
|
|
|
|
|
13 |
|
v |
1 |
v |
1 |
v |
1 |
v1 |
а |
|
б |
|
в |
|
г |
|
G* |
/ G |
|
G13* / G(2)13 |
|
k |
* |
/ k |
12 |
(2)12 |
|
|
|
|||
|
|
|
|
|
12 |
(2)12 |
|
|
|
v1 |
|
v1 |
|
|
|
|
|
|
|
v1 |
|
|
|
д |
|
е |
|
|
|
|
|
|
|
|
ж |
|
|
* |
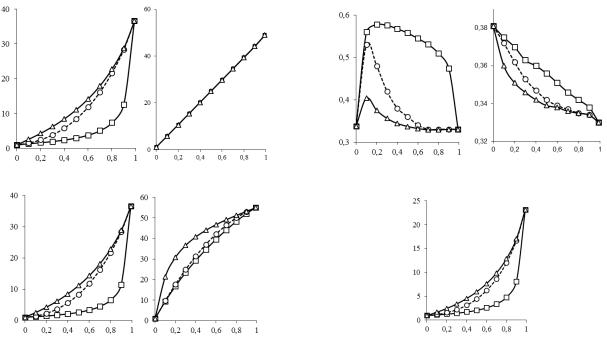
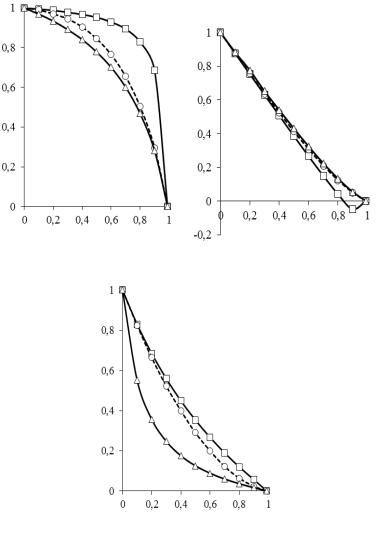
Рис. 2.6. Эффективные модули упругости: модули Юнга |
E |
* |
(а), |
E |
* |
(б), коэффициенты Пуассона |
|||||||
12 |
|
|
||||||||||||
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
||
|
(в), * |
(г), модули сдвига |
G* |
(д), |
G* |
(е), объемный модуль плоской деформации |
k* |
(ж) |
||||||
|
13 |
|
12 |
|
13 |
|
|
|
|
|
|
|
12 |
|
пьезоэлектромагнетика с объемной долей феррита v1
e311* / e(2)311
e333* / e(2)333
v1 |
v1 |
а |
б |
e* |
/ e |
113 |
(2)113 |
v1
в
Рис. 2.7. Эффективные электромеханические константы e311* (а), e333* (б), e113* (в) пьезоэлектромагнетика с объемной долей феррита v1
130
