книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL

– выборочный эксцесс (оценка островершинности (E > 0) или плосковершинности (E < 0) статистического распределения

по отношению к нормальному распределению, для которого он равен 0):

μ

E = 4 4 −3; (2.15) (σx )

– выборочный квантиль xp порядка р – корень уравнения

то есть абсцисса xp точки, лежащей на эмпирической функции распределения Fx (x) и имеющей ординату р; порядок р квантиля xp определяет долю общего числа наблюдений в выборке, результаты которых не превосходят xp .

Выборочную дисперсию аналогично соответствующей дисперсии в теории вероятности также можно представить в виде

Еще раз подчеркнем, что главным отличием числовых характеристик случайных величин от аналогичных им выборочных характеристик, определенных формулами (2.3)–(2.16), состоит в том, что первые являются детерминированными (неслучайными) величинами, а вторые сами являются случайными величинами со своими специфическими законами распределения.

Добавление элементов к выборке или осуществление новой выборки из той же генеральной совокупности приводит к вычислению отличающихся друг от друга числовых характеристик выборок, к изменению эмпирической функции распределения, к изменению вида гистограмм.

Поэтому числовые характеристики эмпирического распределения являются оценками соответствующих числовых характеристик случайной величины.

51

Значение выборочных характеристик состоит в том, что согласно предельным теоремам при n → ∞ они в качестве оценок числовых характеристик изучаемой случайной величины стремятся к истинным значениям этих характеристик, определяемых функцией распределения F(х).

Оценки имеют разброс, поэтому принято различать точечные и интервальные оценки. Если оценка выражается одним числом (приближенным значением параметра), она называется точечной. Оценка, выражаемая двумя числами – концами интервала, накрывающего оцениваемый параметр, называ-

ется интервальной.

Точечных оценок для неизвестной числовой характеристики может быть несколько. Например, в качестве приближенного значения для математического ожидания может быть выбрано и среднее арифметическое, и среднее геометрическое статистического распределения, и медиана.

Получив статистические оценки числовых характеристик распределения изучаемой случайной величины Х (выборочное среднее, выборочную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

Наибольший интерес среди статистических оценок числовых характеристик представляют оценки неизвестных параметров теоретического распределения, которое выбирается в качестве возможной вероятностной модели полученного эмпирического распределения (например, по виду гистограммы относительных частот).

Пусть Θ – статистическая оценка неизвестного параметра Θ теоретического распределения. Извлечем из генеральной со-

ную величину, принимающуювозможныезначения Θ1* ,Θ*2 , ...,Θ*k .

52

Если математическое ожидание Θ не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если M (Θ ) > Θ,

и с недостатком, если M (Θ ) < Θ). Следовательно, необходимым

условием отсутствия систематических ошибок является требование M (Θ ) = Θ.

Статистическая оценка Θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру Θ при любом объеме выборки:

M (Θ ) = Θ.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако несмещенность не является достаточным условием хорошего приближения к истинному значению оцениваемого параметра. Если при этом возможные значения Θ могут значительно отклоняться от среднего значения, то есть дисперсия Θ велика, то значение, найденное по данным одной выборки, может значительно отличаться от оцениваемого параметра. Следовательно, требуется наложить ограничения на дисперсию.

Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется ещеитребование состоятельности.

Состоятельной называется статистическая оценка, которая при п→∞ стремится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п → ∞ ее дисперсия стремится к 0).

Например, относительная частота p = nA / n появления

события А в n независимых испытаниях является несмещенной состоятельной и эффективной оценкой вероятности р = Р{А} этого события (р – вероятность наступления события А в каждом испытании).

53

Легко доказывается, что х представляет собой несмещенную состоятельную и эффективную оценку математического ожиданияM (X ) .

В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Доказано, что

М(Dx* ) = n n−1 D (X ) ,

где D(X) – истинное значение дисперсии генеральной совокупности.

Поэтому часто используют другую, несмещенную, оцен-

ку дисперсии – исправленную дисперсию Dx* испр = s2 (2.7).

Состоятельность – обязательное свойство используемых оценок. Свойство несмещенности является желательным, но многие применяемые оценки этим свойством не обладают.

Результаты математической статистики по точечным оценкам для вероятности события в схеме Бернулли и наиболее распространенного нормального распределения приведены в табл. 2.7.

Окончание табл. 2.7

Указанные в этой таблице свойства оценок для других распределений необходимо заново исследовать.

2.2.1. Вычисление числовых характеристик выборки в MS Excel

Для вычисления точечных оценок основных числовых характеристик выборки Xn ={x1, x2 , x3 , ..., xn }, n ≤ 30, MS Excel

имеет следующие статистические функции (см. прил. 2):

– СРЗНАЧ (число1; число2; ...) – выборочное среднее, см. формулу (2.3);

– МЕДИАНА (число1; число2; . . . ) – медиана, см. (2.4);

– МОДА (число1; число2; . . . ) – мода;

–ДИСП (число1; число2; ...) – исправленная оценка дисперсии, см. (2.7);

–ДИСПР (число1; число2; ...) – смещенная оценка дисперсии, см. (2.5);

–СТАНДОТКЛОН (число1; число2; ... ) – исправленное среднеквадратичное отклонение, см. (2.8);

–СТАНДОТКЛОНП (число1; число2; ... ) – смещенное среднеквадратичное отклонение, см. (2.6);

–СКОС (число1; число2; ...) – коэффициент асиммет-

рии, см. (2.14);

–ЭКСЦЕСС (число1; число2; ...) – эксцесс, см. (2.15).

55

Пример 2.4. Найти оценки числовых характеристик случайной величины по выборке, заданной статистическим рядом

Эти же оценки характеристик можно подсчитать в MS Excel, задав в ячейках А2:А21 значения 20 заданных вариант, в ячейках С2:С6 – текстовые названия характеристик, а D2:D6 – соответствующие статистические функции для их вычисления. Результат такоговычисления приведен в табл. 2.8.

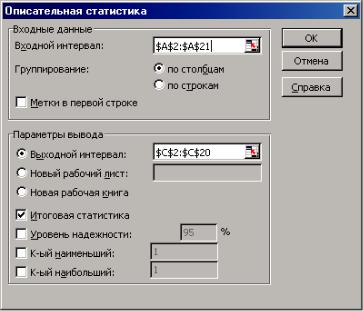
В MS Excel представление выборки с помощью числовых точечных оценок дает также инструмент «Описательная статистика», доступный из окна «Анализ данных». Для рассматриваемого примера входим в меню «Сервис» → «Анализ данных» → «Описательная статистика» (см. рис. 2.9), где в качестве входного интервала указываем нужные ячейки столбца А с вариантами выборки, указываем выходной интервал ячеек для результатов и заказываем «Итоговую статистику», результаты приведены в табл. 2.9.

Рис. 2.9. Задание данных в меню «Описательная статистика»

Пример 2.5. Для 5 выборок, полученных в примере 2.2, оценить числовые характеристики с помощью MS Excel.

Решение. Для таблицы, изображенной на рис. 2.2, задаемданные в меню «Описательная статистика» согласно рис. 2.9, получаемрезультатыввидеотредактированнойтаблицы2.10.

57

Их анализ показывает, что мы действительно нашли только оценки заданных в примере 2.2 параметров нормального закона распределения: а = 2,1, σ = 0,1. Их выборочные зна-

чения среднего (2.0794, 2.0257, 2.1185, 2.1223, 2.1003) и стандартного отклонения (0.1195, 0.1145, 0.1237, 0.1206, 0.0978)

имеют разброс и эти оценки сами являются случайными величинами.

Таблица 2.10

Окончание табл. 2.10

2.3. Точечная оценка неизвестных параметров распределения

Из статистических оценок числовых характеристик распределения случайной величины Х важную роль играет их частная разновидность– точечные оценки неизвестных параметров распределения F(x).

Предположим, что экспериментатору из каких-либо соображений или по виду гистограммы относительных частот известен класс функций распределения (нормальных, показательных, биномиальных и т.д.), к которому может принадлежать функция распределения вероятностей выборочно исследуемой случайной величины, а параметры, определяющие этот закон, неизвестны.

Требуется по результатам выборочного эксперимента оценить эти параметры, то есть найти их приближенные значения. Рассмотрим два наиболее распространенных метода построения приближенных значений параметров в виде точечных оценок (каждый параметр оценивается одним числом – точкой на оси его возможных значений): метод максимального правдоподобия и метод моментов.

2.3.1. Метод наибольшего правдоподобия

Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х1, х2, …, хп, среди которых могут быть одинаковые значения, тогда вероятность по-

59

явления каждого значения равна 1/n. Предположим, что нам известен закон распределения этой величины, определяемый параметром Θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.

Пусть р(хi, Θ) – вероятность того, что в результате испытания величина Х примет значение хi. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента Θ, определяемую по формуле

где p(xi,Θ) – вероятность реализации значения xi (i = 1, 2, …, n) согласно рассматриваемому закону распределения дискретной случайной величины.

Тогда в качестве точечной оценки параметра Θ принимают такое его значение Θ = Θ(х1, х2, …, хп), при котором функция правдоподобия достигает максимума. Оценку Θ называ-

ют оценкой наибольшего правдоподобия.

Поскольку функции L и ln(L) достигают максимума при одном и том же значении Θ, удобнее искать максимум ln(L) –

логарифмической функции правдоподобия. Для этого нужно:

1) найти производную dln (L) ; dΘ

2)приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти корни этого уравнения;

3)выбрать решение, которое соответствует максимуму функции правдоподобия, для чего найти вторую производную

d2 ln (L) : если она отрицательна для рассматриваемого корня, d Θ2

то это – точка максимума.

Пример 2.6. Для выборки, содержащей n целочисленных положительных значений xi, найти оценку параметра а распределения Пуассона методом максимального правдоподобия.

60