книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL

между нею и гистограммой статистического распределения неизбежны некоторые расхождения.

Естественно возникает вопрос: объясняются ли эти расхождения только случайными причинами или они являются существенными и связаны с тем, что плохо подобрана вероятностная модель. Для ответа на этот вопрос производится проверка нулевой гипотезы с помощью так называемых критериев согласия.

Принципы построения таких критериев и методика проверки остаются практически такими же, как и в случае параметрических гипотез. Для того чтобы принять или опровергнуть гипотезу H0, рассматривают некоторую выборочную статистику (критерий), характеризующую степень расхождения теоретического и статистического распределений. По распределению этой статистики, полученному в предположении истинности нулевой гипотезы, и заданному уровню значимости находятся критические значения и сравниваются с наблюдаемым значением критерия.

Наиболее распространенными из непараметрических критериев значимости являются критерий согласия χ2 Пирсона и λ −критерий А.Н. Колмогорова. Мы подробно рассмотрим здесь только критерий согласия Пирсона. Относительно критерия Колмогорова отметим, что он выгодно отличается простотой вычисления наблюдаемого значения от критерия χ2, но для принятия гипотезы необходимо знать критические точки распределения Колмогорова, не представленные в MS Excel. В пакете STATISTICA при подборе закона распределения для выборки можно одновременно использовать подсчет наблюдаемых значений критериев Колмогорова и Пирсона.

111

На практике приходится сталкиваться с тем, что для одной и той же выборки удовлетворительные результаты аппроксимации распределения дают разные законы. В этом случае следует выбирать тот закон, который дает меньшее значение используемого критерия.

Зная теоретический (гипотетический) закон распределения, можно найти теоретические вероятности попадания случайной величин в каждый из разрядов: p1, p2 , ..., pm .

Проверяя согласованность теоретического и статистического распределений, будем исходить из расхождений между теоретическими вероятностями pi и наблюденными частотами

pi . Естественно выбрать в качестве меры расхождения между ними сумму квадратов отклонений pi − pi , взятых с некоторыми значениями веса ci :

m

K = ∑ci ( pi − pi )2.

i=1

Коэффициенты ci (весы разрядов) вводятся потому, что

отклонения нельзя считать равноценными по значимости для всех разрядов: одно и то же по абсолютной величине откло-

112

нение pi − pi может быть малозначительным, если сама вероятность pi велика, и очень заметным, если она мала. Поэтому естественно значения веса взять обратно пропорциональными вероятностям pi разрядов.

К. Пирсон показал, что если положить сi = n / pi , то при

больших значениях n закон распределения величины K практически не зависит от функции распределения наблюдаемой случайной величины и от числа опытов, при увеличении их числа приближается к распределению χ2 с ν = m − r −1 сте-

пенями свободы ( m −число разрядов, r − число параметров гипотетической функцииF(x) , оцениваемых по выборке). Та-

Вдальнейшем мы эту статистику будем обозначать

χ2m−r −1 и для удобства вычислений записывать в виде:

Критерий χ2 использует тот факт, что случайная величина

ni −npi , i = 1, 2, …, m имеет распределение, близкое к стан- npi

дартному нормальномуN (0;1). Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов выполнялось условие npi ≥ 5. Если в некоторых интервалах это условие

невыполняется, тоихследует объединитьссоседними.

Таким образом, процедура применения критерия согласия

χ2 (Пирсона) состоит из следующих этапов:

1.По выборке найти точечные оценки неизвестных параметров предполагаемого закона распределения F(x), если они

неизвестны.

113

2.Составить группированный статистический ряд с достаточной длявыполнения условия npi ≥ 5 частотой ni разрядов.

3.Вычислить теоретические вероятности pi попадания

случайной величины в каждый из разрядов.

4. Вычислить выборочное значение статистики критерия

H0 следует отклонить.

Критерий χ2 сконструирован таким образом, что чем

ближе к нулю наблюдаемое значение критерия, тем вероятнее, что нулевая гипотеза справедлива. Поэтому критическая область критерия правосторонняя.

Пример 3.9. В течение 100 дней фиксировалось число автомобильных аварий в некотором районе города. Получены следующие данные:

Проверить гипотезу о том, что число аварий имеет распределение Пуассона. Уровень значимости принять рав-

ным 0,05.

Решение. Согласно условию гипотетическая функция распределения имеет вид

114

рий в течение 100 дней вычислим по формуле Пуассона, подставив вместо параметра λ его выборочную оценку λ :

Результаты дальнейших вычислений сведем в табл. 3.4, представляющую проверку гипотезы о соответствии числа аварий распределению Пуассона (в пренебрежении условием npi ≥ 5 для xi = 5):

Таблица 3.4

Выше условие npi ≥ 5 для xi = 5 не выполнено, объединим два последние подынтервала, сложив соответствующие значения ni и pi . В результате имеем уточненную табл. 3.4*

χнабл2 = 2,35 < 7,815 = (χ2 )правкр, α,

для отклонения нулевой гипотезы при уточненной процедуре ее проверки нет оснований.

Значит, с вероятностью ошибки 0,05 принимаем, что число автомобильных аварий в этом районе распределено по закону Пуассона с параметром λ = 2,1.

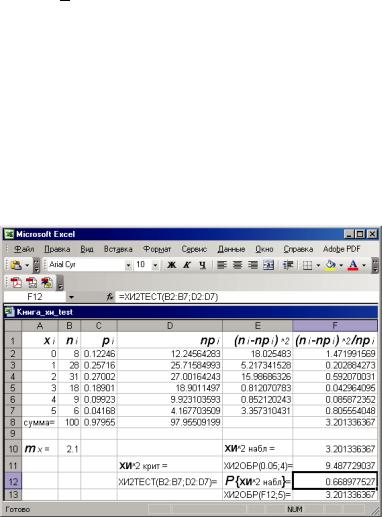
Выполним проверку этой гипотезы с использованием MS Excel (рис. 3.10). В ячейках А1:F1 зададим названия переменных из первого столбца табл. 3.4, в ячейках А2:А7 – значения xi , в ячейках В2:В7 – значения ni , в ячейке В8 нахо-

дим число дней наблюдения = СУММ(В2:В7), затем в ячейке В10 по методу моментов находим оценку параметра рас-

116

пределения Пуассона с помощью математической функции

СУММПРОИЗВ(массив1; массив2; …) (рис. 3.11):

λ = mx = 1n ∑i ni xi = СУММПРОИЗВ(A2:A7; B2:B7)/100 = 2,1.

Для вычисления теоретических вероятностей pi в ячейке

С2 (рис. 3.12) задаем вызов функции =ПУАССОН(A2;$B$10; ЛОЖЬ), а затем копируем эту формулу протаскиванием в ячейки С3:С7 (здесь задан фиксированный адрес ячейки В10, который не меняется при копировании формулы в другие ячейки в отличие от адреса ячейки А2).

Суммирование вероятностей pi в ячейке С8 дает резуль-

тат, отличающийся от единицы, что связано с приближенным соответствием результатов наблюдений теоретической модели распределения Пуассона.

Рис. 3.10. Результаты вычислений для критерия согласия χ2

117

Вячейку D2 задаем формулу =100* С2 и копируем ее

вячейки D3:D7, в ячейку Е2 – формулу =(B2–D2)^2 и копиру-

ем ее в Е3:Е7, в ячейку F2 – формулу =E2/D2 и копируем ее в F3:F7.

Суммированием содержимого ячеек F2:F7 находим несколько отличающееся (из-за ошибок округления при вычислении значений в табл. 3.4) наблюдаемое значение критерия

χнабл2 = 3,20.

Для подсчета значения правосторонней критической точки для уровня значимости α = 0,05 и числа степеней свободы

χнабл2 < (χ2 )правкр, α, основная гипотеза о соответствии заданной выборки закону распределения Пуассона принимается.

Уточненный анализ этой гипотезы при выполнении условия npi ≥ 5 для xi = 5 аналогичен по результатам вышеприведенному анализу при ручном счете.

Рис. 3.11. Меню вызова функции СУММПРОИЗВ(массив1; массив2; …)

118

Рис. 3.12. Меню вызова функции ПУАССОН (х; среднее; интегральная)

Рис. 3.13. Меню вызова функции ХИ2ОБР (вероятность; степени свободы)

В MS Excel для проверки непараметрических статистических гипотез по критерию Пирсона служит также специализированная статистическая функция ХИ2ТЕСТ(фактичес-

кий_интервал; ожидаемый_интервал) – возвращает для представленной в выборке случайной величины Х значение вероятности P{x ≥ χнабл2 } для χ2-распределения согласно критерию Пирсона. Аргументами этой функции являются:

119

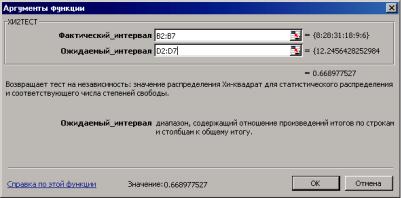
фактический интервал – это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

ожидаемый интервал – это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.

Для рассматриваемого примера фактический интервал соответствует значениям ni , ожидаемый интервал – значениям npi , вызов этой функции в ячейке F12 = XИ2ТЕСТ(B2: :B7;D2:D7)

даетвероятность P{x ≥ χнабл2 = 3,20}= 0,669 (рис. 3.14).

Рис. 3.14. Меню вызова функции ХИ2ТЕСТ (фактический интервал; ожидаемый интервал)

Для проверки этого утверждения в ячейке F13 (см. рис. 3.10) с помощью формулы =ХИ2ОБР(F12;5) имеем ранее вычисленное в ячейке F8 значение χнабл2 = 3,20.

Рассмотрим типичную полную статистическую обработку экспериментальных результатов для одномерной выборки с подбором непрерывного закона распределения по критерию Пирсона.

120