книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL

Построенную величину Х можно трактовать, например, как количество колес, ежедневно поступавших на шиноремонтный участок автопредприятия в течение 50 дней.

Этот пример демонстрирует, что имеющиеся здесь 3 элемента со значениями х > 13 являются естественными для данного распределения и их нельзя отбрасывать в ходе рецензирования выборки, хотя среднее выборочное значение за время наблюдения приближенно равно 4.

Гладкой сплошной линией на рис. 2.1 также показана теоретическая кривая f(x) плотности показательного распределения с параметром λ = 0,2337, аппроксимирующая (сглаживающая) построенную гистограмму.

По аналогии с функцией распределения F(x) случайная величина X для выборки Xn = {x1, x2 , x3 , ..., xn } можно задать

некоторую функцию, определяющую относительную частоту события X < x.

Выборочной (эмпирической) функцией распределения

называют функциюFn (x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,

где пх – число вариант, меньших х; п – объем выборки.

В отличие от эмпирической функции распределенияFn (x), найденной опытным путем согласно (2.2), гипотети-

чески существующую функцию распределения F(x) гипотетической генеральной совокупности называют теоретической функцией распределения. F(x) определяет вероятность события X < x, а Fn (x) – его относительную частоту в выборке объема n. При достаточно больших п из теорем Бернулли и Гливенко следует, что Fn (x) стремится по вероятности к F(x).

41

В MS Excel для графического представления выборок в виде гистограмм используется инструмент «Гистограмма», доступный из окна «Анализ данных». Подробный пример использования этогоинструмента описан в нижеследующем примере.

2.1.1. Построение гистограмм вручную и в MS Excel

Рассмотрим практическое построение гистограмм. Пример 2.3. Представить выборку 55 наблюдений в виде

статистического ряда, используя 7 интервалов:

17 19 23 18 21 15 16 13 20 18 15 20 14 20 16 14 20 19 15 19

16 19 15 22 21 12 10 21 18 14 14 17 16 13 19 18 20 24 16 20

19 17 18 18 21 17 19 17 13 17 11 18 19 19 17

Построить гистограммы относительных и накопленных частот.

Решение. Размах выборки: R = 24 – 10 = 14. Длина разряда h = 14/7 = 2. Результаты группировки сведем в табл. 2.4:

Таблица 2.4

F (x) = 1 при x > 24.

Проанализируем данные этого примера с помощью табличного процессора MS Excel, построим группированный статистический ряд и графики: введем все данные в столбец А

43

(см. прил. 1), затем отсортируем их в порядке возрастания («Данные» → «Сортировка», рис. 2.3).

нов» = разрядов = частичных интервалов (их можно не задавать совсем и здесь и в диалоге построения гистограммы – процессор сам ихназначит), полученная таблица представлена нарис. 2.5.

Рис. 2.4. Полученный вариационный ряд

44

Рис. 2.5. Таблица с заданными «карманами»

Теперь все готово для построения гистограммы относительных частот и кумулятивной кривой (в Excel – интегрального процента). Входим в меню «Сервис» → «Анализ данных» → «Гистограмма» (рис. 2.6), где в качестве входного интервала указываем нужные ячейки столбца А, указываем нужный интервал «карманов» – ячейки столбца В.

Получаем следующий группированный статистический ряд (табл. 2.5 с транспонированной матрицей относительно матрицы табл. 2.4) в ячейках таблицы F1:H9, совпадающий по частотам с приведенным выше рядом при ручном счете (см. левые три столбца табл. 2.5), гистограмму частот и кумулятивную кривую (накопленный процент) (рис. 2.7). Но для обеспечения этого совпадения пришлось сдвинуть границы «карманов» от целых значений (на практике рекомендуется

45

брать середины «карманов», отличающиеся только в последних значениях результаты для этого случая приведены в трех правых столбцах табл. 2.5).

Рис. 2.6. Диалог определения гистограммы

46

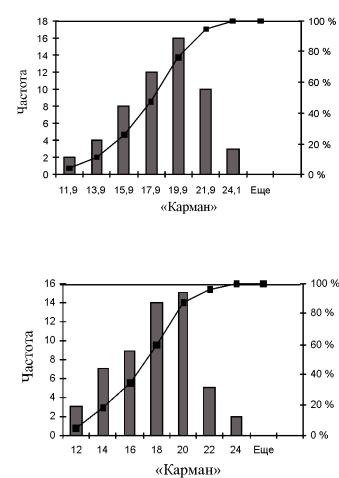
Если же задать реальные границы карманов целыми числами, то получим существенно отличающийся статистический ряд (табл. 2.6) и соответственно отличающиеся графики гистограмм (рис. 2.8).

Рис. 2.7. Гистограмма частот и кумулятивная кривая:

– частота; – интегральный процент

Рис. 2.8. Вариант гистограммы частот и кумулятивной кривой: – частота; – интегральный процент

47

Приведенный пример неоднозначности построения статистического ряда связан со следующими обстоятельствами:

1.Случайная переменная принимает целые значения, совпадающие с границами «карманов».

2.В отечественной литературе в основном используется определение функции распределения и эмпирической функции

распределения как вероятности события {X < x}, см. (2.2). Часто в иностранной литературе (и в Excel) используется неравенство {X ≤ x}. Поэтому по разному решается вопрос, включать или не включать попадание в «карман» значений, совпадающих с правой границей «кармана».

3.При построении статистического ряда вручную для последнего варианта и последнего «кармана» было нарушено условие X < x, фактически использовано X ≤ x, что свидетельствует о преимуществе использования этого события.

4.Для целочисленных границ «карманов» предпочтительнее в качестве таковых указывать координаты середин «карманов».

В практическом анализе статистических данных эти отличия редко проявляются так значительно. Кроме этого, нужно принимать во внимание, что мы имеем дело с приближенными случайными данными.

48

2.2. Числовые характеристики статистического (выборочного) распределения

Числовые характеристики случайных величин играют важную роль в их интерпретации, являясь детерминированными (неслучайными) величинами, характеризующими центр случайного рассеяния, показатели рассеяния, вид кривой плотности распределения и т.п.

Каждой числовой характеристике случайной величины можно поставить в соответствие ее статистическую аналогию (статистическую оценку), которая в силу случайности выборки сама являетсяслучайнойвеличинойсосвоимзакономраспределения.

Чаще всего в качестве таких статистических аналогий ис-

пользуются следующие выборочные числовые характери-

стики (статистики) – величины, вычисляемые по выборке (ниже даны формулы для негруппированных и группированных данных, для отличия выборочных характеристик от аналогичных теоретических числовых характеристик будем в основном использовать в качестве верхнего индекса символ

«*», делая исключение для оценки mx ≡ x):

– выборочное среднее (статистическое среднее – оценка математического ожидания):

–мода статистического распределения– такое значение случайной величины, которому соответствуетнаибольшаячастотапоявления;

–медиана – такое значение xмед, для которого

– выборочная дисперсия (смещенная оценка):

49

– выборочное среднеквадратическое отклонение:

– выборочный коэффициент вариации – безразмерная относи-

тельная квадратичная оценки рассеяния:

– размах выборочный – простейшая размерная оценка рассеяния:

– выборочный начальный момент порядка k (k = 1, 2, 3, …):

– выборочный центральный момент порядка k (k = 1, 2, 3, …):

– выборочный коэффициент асимметрии (для симметричных распределений равен 0):

μ

As = (σ 3)3 ; (2.14)

x

50