
книги / Математический анализ динамических моделей
..pdf
|
3 |
|
2 2 |
|
|
3 3 |
1 |
|
|
2 |
1 |
1 |
||||||||
9. |
|
3 |
|
1 |
|
|
21. |
|
3 |
2 |
2 |
|
33. |
|
1 |
0 |
|
|
|
|
|
|
1 |
|
|
|
1 |
||||||||||||||
|
|
1 |
|
2 0 |
|
|
|
1 |
|
2 |
0 |
|
|
|
1 |
1 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
1 1 |
|
|
|
0 1 1 |
|
|
2 |
1 2 |
|
|||||||||
10. |
|
1 |
0 |
|
|
|
22. |
|
1 |
1 |
0 |
|
|
34. |
|
1 |
0 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
1 0 |
|
|
|
|
|
2 |
0 |
3 |
|
|
|
|
|
2 1 |
|
|
|
1 |
|
|
|
|
|
|||||||||
|
0 |
1 1 |
|
|
|
4 2 2 |
|
|
2 |
0 1 |
||||||||||
11. |
|
1 |
0 |
|
|
|
23. |
|
1 |
3 |
|
|
|
35. |
|
1 |
1 |
0 |
|
|
|
1 |
|
|
1 |
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
2 3 |
|
|
|
3 3 1 |
|
|
|
1 |
||||||||||
|
0 |
1 0 |
|
|
|
2 1 0 |
|
|
|
|
1 |
0 3 |
||||||||
12. |
|
0 |
0 |
0 |
|
|
24. |
|
0 |
2 |
|
|
|
36. |
|
1 |
2 |
0 |
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
0 |
0 2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
0 0 2 |
|
|
|
|
1 |
|||||||||
Упражнение 3. Исследовать на устойчивость нулевое решение ЛРУ сведением характеристического уравнения и исследование его: 1) методом Рауса – Гурвица; 2) методом Льенара – Шипара; 3) методом Михайлова.
1. |
x(t 3) x(t 2) 8x(t 1) 12x(t) 0, |
t 0,1,2,... |
|
|||
2. |
11x(t 4) 8x(t 3) 8x(t 2) 4x(t 1) x(t) 0, |
t 0,1,2,... |
||||
3. |
x(t 4) x(t 3) x(t) 0, |
t 0,1,2,... |
|
|
|
|
4. |
12x(t 4) 3x(t 3) 2x(t 2) 2x(t 1) 2x(t) 0, |
t 0,1,2,... |
||||
5. |
7x(t 4) 4x(t 3) 30x(t 2) 4x(t 1) 3x(t) 0, |
t 0,1,2,... |
||||
6. |
x(t 5) x(t 1) x(t) 0, |
t 0,1,2,... |
|
|
|
|
7. |
x(t 5) x(t 2) x(t) 0, |
t 0,1,2,... |
|
|
|
|
8. |
x(t 5) x(t 2) x(t) 0, |
t 0,1,2,... |
|
|
|
|
9. |
x(t 4) 2x(t 3) 4x(t 2) 2x(t 1) 5x(t), |
t 0,1,2,... |
||||
10. x(t 4) x(t 2) 2x(t 1) 2x(t) 0, |
t 0,1,2,... |
|
||||
11. x(t 4) x(t) 0, |
t 0,1,2,... |
|
|
|
||
41
12.x(t 4) 2x(t 3) 3x(t 2) 2x(t 1) x(t) 0, |
t 0,1,2,... |
||||||||
13. |
2x(t 4) 5x(t 3) 5x(t 2) 2x(t) 0, |
t 0,1,2,... |
|||||||
14.x(t 4) 4x(t 2) 3x(t) 0, |
|
t 0,1,2,... |
|
|
|||||
15. |
5x(t 5) x(t) 0, |
t 0,1,2,... |
|
|
|
|
|
||
16. |
5x(t 5) 4x(t) 0, |
t 0,1,2,... |
|
|
|
|
|||
17. |
4x(t 3) 2x(t 2) x(t) 0, |
t 0,1,2,... |
|
|
|||||
18. |
27x(t 3) 27x(t 2) 12x(t 1) 2x(t) 0, |
t 0,1,2,... |
|||||||
19. |
4x(t 3) 10x(t 2) 4x(t 1) 3x(t) 0, |
t 0,1,2,... |
|||||||
20. |
4x(t 3) 3x(t 2) x(t 1) x(t) 0, |
t |
0,1,2,... |
|
|||||
21. |
4x(t 3) |
2x(t 2) 4x(t 1) 3x(t) 0, |
t 0,1,2,... |
||||||
22. |
27x(t 3) 9x(t 2) 2x(t) 0, |
t 0,1,2,... |
|
|
|||||
23. |
4x(t 3) |
x(t 2) 2x(t 1) x(t) 0, |
t 0,1,2,... |
|
|||||
24. |
2x(t 3) |
x(t 2) x(t) 0, |
t 0,1,2,... |
|
|
|
|||
25.x(t 3) 5x(t 2) 3x(t 1) x(t) 0, |
t 0,1,2,... |
|
|||||||
26. |
2x(t 3) |
x(t 2) x(t) 0, |
t 0,1,2,... |
|
|
|
|||
27. |
27x(t 3) 9x(t 2) 2x(t) 0, |
t 0,1,2,... |
|
|
|||||
28.x(t 5) 4x(t 4) 16x(t 3) 25x(t 2) 13x(t 1) 9x(t) 0, t 0,1,2,...
29.x(t 5) 3x(t 4) 10x(t 3) 22x(t 2) 23x(t 1) 12x(t) 0, t 0,1,2,...
30.x(t 5) 5x(t 4) 15x(t 3) 48x(t 2) 44x(t 1) 74x(t) 0, t 0,1,2,...
31.x(t 5) 2x(t 4) 14x(t 3) 36x(t 2) 23x(t 1) 68x(t) 0, t 0,1,2,...
32. |
2x(t 4) |
x(t 3) x(t 2) x(t 1) x(t) 0, |
t 0,1,2,... |
|
33. |
2x(t 4) 2x(t 3) x(t 2) 2x(t 1) x(t) 0, |
t 0,1,2,... |
||
34.2x(t 4) |
3x(t 3) 4x(t 2) 2x(t 1) x(t) 0, |
t 0,1,2,... |
||
42 |
|
|
|
|
35.x(t 4) x(t 3) 4x(t 2) x(t 1) x(t) 0, t |
0,1,2,... |
36. x(t 4) 2x(t 3) 4x(t 2) 5x(t 1) 5x(t) 0, |
t 0,1,2,... |
Упражнение 4. Исследовать на устойчивость нулевое решение ЛДРУ: либо используя метод D-разбиения, либо используя действительные корни квазиполинома.
37. |
x (t) x (t) |
x(t 1), |
t 0, |
|
|||
|
x( ) ( ), |
|
|
0. |
|
||
38. |
x (t) x (t) x(t 1) 0, |
t 0, |
|||||
|
x( ) ( ), |
|
|
|
0. |
||
|
|
|
|
|
|
|
t 0, |
39. |
x (t) x (t 1) x(t 1) 0 |
||||||
|
|
|
|
|
|
0. |
|
|
x( ) ( ), |
x ( ) ( ), |
|
||||
|
|
|
|
|
|
|
t 0, |
40. |
x (t) x (t 1) x(t 1) 0, |
||||||
|
|
|
|
|
|
0. |
|
|
x( ) ( ), |
x ( ) ( ), |
|
||||
41. |
x (t) x(t |
1) 0, |
t 0, |
|
|
||
|
x( ) ( ), |
|
0. |
|
|
||
42. |
x (t) x(t / 2), |
t 0, |
|
|
|||
|
x( ) ( ), |
|
0. |
|
|
||
43. |
x (t) x(t) x(t / 2) 0, |
t 0, |
|||||
|
x( ) ( ), |
|
|
|
|
0. |
|
44. |
x (t) x(t) x(t / 2) 0, |
t 0, |
|||||
|
x( ) ( ), |
|
|
|
|
0. |
|
|
|
|
|
|
|
t 0, |
|
45. |
x (t) x (t 1) x(t) 0, |
||||||
|
|
|
|
|
0. |
||
|
x( ) ( ), x ( ) ( ), |
||||||
46. |
x (t) x(t 1), |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
||
43
|
|
|
|
|
|
|
|
t 0, |
|
47. |
x (t) x (t 1) x(t 1) 0, |
||||||||
|
|
|
|
|
|
|
0. |
||
|
x( ) ( ), |
x ( ) ( ), |
|
||||||
|
|
|
|
|
|
|
|
t 0, |
|
48. |
x (t) x (t 1) x(t 1) 0, |
||||||||
|
|
|
|
|
|
|
0. |
||
|
x( ) ( ), |
x ( ) ( ), |
|
||||||
|
|
|
|
|
|
|
t 0, |
|
|
49. |
x (t) x (t 1) x(t) 0, |
|
|
||||||
|
|
|
( ), |
|
0. |
|
|||
|
x( ) ( ), x ( ) |
|
|
||||||
50. |
x (t) x(t) x(t 1) |
1, |
t 0, |
|
|||||
|
x( ) ( ), |
|
|
|
0. |
|
|||
51. |
x (t) x (t) x(t 1) 0, |
|
t 0, |
|
|||||
|
x( ) ( ), |
|
|
|
|
0. |
|
||
52. |
x (t) x(t 2 ), |
t 0, |
|
|
|
|
|||
|
x( ) ( ), |
|
0. |
|
|
|
|
||
53. |
x (t) e x(t |
1), |
t 0, |
|
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
||
54. |
x (t) 2x(t ln(2)), |
t 0, |
|
|
|||||
|
x( ) ( ), |
|
|
0. |
|
|
|||
|
|
|
|
|
|
|
t 0, |
|
|
55. |
x (t) x (t 2 ) 0, |
|
|
||||||
|
|
|
( ), |
|
0. |
|
|||
|
x( ) ( ), x ( ) |
|
|
||||||
|
|
|
|
|
|
|
t 0, |
|
|
56. |
x (t) x (t 2 ) 0, |
|
|
||||||
|
|
|
( ), |
|
0. |
|
|||
|
x( ) ( ), x ( ) |
|
|
||||||
|
|
|
|
|
|
|
|
|
t 0, |
57. |
x (t) x (t 1) 2 x(t 1) 0, |
||||||||
|
|
|
|
|
|
|
|
0. |
|
|
x( ) ( ), |
x ( ) ( ), |
|
||||||
58. |
x (t) x (t) 100 x(t 1) 0, |
t 0, |
|||||||
|
x( ) ( ), |
|
|
|
|
|
0. |
||
|
|
|
|
|
|
|
|
|
t 0, |
59. |
x (t) 50 x (t 1) 50 x(t) 0, |
||||||||
|
|
|
|
|
|
|
|
0. |
|
|
x( ) ( ), |
x ( ) ( ), |
|
|
|||||
44
|
|
|
|
|
|
|
t 0, |
60. |
x (t) 50 x (t 1) 50 x(t 1) 0, |
||||||
|
|
|
|
|
|
0. |
|
|
x( ) ( ), |
x ( ) ( ), |
|
|
|||
|
|
|
|
|
|
t 0, |
|
61. |
x (t) 50 x (t 1) 50 x(t) 0, |
||||||
|
|
|
|
|
0. |
||
|
x( ) ( ), |
x ( ) ( ), |
|
||||
62. |
x (t) x (t) 100 x(t 1) 0, |
t 0, |
|
||||
|
x( ) ( ), |
|
|
|
0. |
|
|
63. |
x (t) x(t ) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
64. |
x (t) x(t ) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
65. |
x (t) x(t ) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
66. |
x (t) x(t 2 ) 0, |
|
t 0, |
|
|
|
|
|
x( ) ( ), |
|
|
0. |
|
|
|
67. |
x (t) x(t ) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
68. |
x (t) x(t 2 ) 0, |
|
t 0, |
|
|
|
|
|
x( ) ( ), |
|
|
0. |
|
|
|
69. |
x (t) x(t ) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
70. |
x (t) x(t 2 ) 0, |
|
t 0, |
|
|
|
|
|
x( ) ( ), |
|
|
0. |
|
|
|
71. |
x (t) x(t / 2) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
|
0. |
|
|
|
72. |
x (t) x(t 1) 0, |
t 0, |
|
|
|
||
|
x( ) ( ), |
|
0. |
|
|
|
|
45

Индивидуальное задание № 4
Производственные функции
Мультипликативная производственная функция валового выпуска РФ (млрд руб.) в зависимости от стоимости основных производственных фондов (млрд руб.) и числа занятых в народном хозяйстве (млн человек) по данным за 1960–1994 гг. (все стоимостные показатели даны в сопоставимых ценах для этого периода) имеет вид:
y ak L |
|
|
a 0,931; |
0,594; |
0,539. |
Требуется, выбрав а, , по формулам (1):
1.Проверить аксиомы ПФ.
2.Построить график поверхности ПФ, изокванты, изоклинали.
3.Вычислить:
а) средние продукты капитала K и труда L ; б) предельные продукты капитала k и труда L ;
в) эластичности выпуска по капиталу EK (y) и труду EL (y); г) предельную норму замещения труда и капиталом h;
д) эластичность замещения труда капиталом .
|
|
a 0,931 0,01n |
0,594 0,01n |
|||||||||||||||||
где n – номер варианта. |
|
|
|
|
|
|
|
|
|
|||||||||||
K |
|
y |
; |
|
L |
|
y |
; |
K |
y |
|
; |
|
|||||||
K |
|
L |
K |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ek (y) |
|
y |
|
y |
; |
|
|
|
|
EL (y) |
y |
|
|
y |
|
|
; |
|||
|
K |
|
|
|
|
|
L |
L |
||||||||||||
|
|
|
|
|
K |
|
|
|
|
|
|
|
||||||||
|
K |
; |
|
|
d |
h |
|
|
|
|
|
|
|
|
|
|
|
|||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
dh |
|
|
|
|
|
|
|
|
|
|
|
||||
0,539 0,01n, |
(1) |
L y ;L
h dK yL '; dL yK '
46

Индивидуальное задание № 5
Моделирование рыночной динамики
Упражнение 1. Простейшая динамическая паутинообразная модель определяется исходя из зависимостей. Спрос в момент времени t:
Dt α aPt ut ,
где a 0, ut – случайная величина с математическим ожиданием M(ut) = 0 и средним квадратичным отклонением σ(ut ) σu const 0.
Предложение товара в момент времени t:
St β bPt 1 vt ,
где vt – случайная величина с M(vt) = 0 и σ(vt ) σv |
const 0. |
При заданном P0 (табл. 1) из равенства Dt St |
получаем |
Pt ba Pt 1 a1(α β) ut a vt .
Вычислите P1, P2 и т.д., построить график зависимости, выбрав , a, β, b из табл. 1. Проверьте условия устойчивости, сходимости к предельной цене (цене равновесия). Постройте паутинообразный график.
|
|
|
|
Таблица 1 |
|
|
|
|
… |
|
|
Вариант |
1 |
2 |
36 |
||
|
|
|
|
|
|
|
100.01 |
100.02 |
… |
100.36 |
|
|
|
|
|
|
|
a |
5.6 |
5.5 |
… |
2.1 |
|
|
|
|
|
|
|
|
0.1 |
0.2 |
… |
3.6 |
|
|
|
|
|
|
|
b |
3.6 |
3.55 |
… |
1.85 |
|
|
|
|
|
|
|
P0 |
10 |
10.1 |
… |
13.6 |
|
|
|
|
|
|
|
47
Упражнение 2. Динамическая непрерывная модель Вальраса – Эванса – Самуэльсона с учётом дискретного запаздывания цены предложения определяется исходя из зависимостей:
|
D(t) α aP(t), |
|
S(t) β bP(t τ), |
P(ξ) P0(ξ) |
при ξ 0, P0(ξ) – известная функция, |
|
dP |
(D S). |
|
dt |
|
Отсюда получаем, что
dPdt(t) λaP(t) λbP(t τ) λ(α β),
P(ξ) P0(ξ) при ξ 0,
где a, , b, и P0 смотри в табл. 1, взять любое . Проверьте условия устойчивости, сходимость к предельной цене (цене равновесия). Постройте график траекторий. Если спрос D и предложения товара S зависит от дохода M:
D α aP a1M a2M ,
S(t) β bP(t τ) b1M (t) b2M (t),
то модель принимает вид:
dPdt(t) aP(t) bP(t ) ( ) a1M (t) a2M (t),
P(ξ) P0(ξ) при ξ 0,
где a1 a1 b1 , a2 a2 b2.
Выбрав a, , b, и P0 из табл. 1, P0(ξ) 0, если ξ 0, постройте график траекторий в следующих случаях:
M (t) η(t) – функция Хевисайда;
M (t) At B , А = 0,931 + 0,01n, B = 0,605 + 0,01n;
M (t) Aexp(αt), = 0,539–0,01n;
|
M (t) A(1 sin(ωt)), |
= 0,594 + 0,01n. |
Взять любые значения λ, a1, a2 .
48
Индивидуальное задание № 6
Линейные модели макроэкономики
Упражнение 1. Простейшая модель воспроизводства чистого
внутреннего продукта (ЧВП), имеет вид: |
|
|
|
|
|
|
|
||||||
|
Y (t) |
B dY (t) |
C(t), или dY (t) ρY (t) ρC(t), |
|
|
|
|
||||||
|
|
|
dt |
|
dt |
|
|
|
|
|
|
|
|
где B – капиталоемкость НД (акселератор, мощность акселератора, |
|||||||||||||
приростная капиталоемкость, коэффициент инвестиций), |
ρ |
|
1 |
|
техно- |
||||||||
|
B |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
логический темп прироста (индекс роста), C(t) |
– |
конечное потребление, |
|||||||||||
Y (t) – ЧВП. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти |
Y (t) |
в |
следующих |
случаях: |
C(t) 0, |
C(t) C(0)δ(t), |
|||||||
C(t) C(0) const, C(t) C(0)er t , C(t) C(0)(1 sin(2πt)), C(t) C t C(0). |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Взять значения |
B |
в зависимости |
от |
номера |
|
в |
группе: |
||||||
B 3,01; |
3,02; |
; |
3,36. |
Принять |
r ρ0 , |
r ρ0 и |
|
r ρ0 , где |
|||||
|
C(0) |
|
|
|
|
|
|
|
|
|
|
|
|
ρ0 ρ 1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (0) |
|
|
|
|
|
|
|
|
|
|
|
|
Упражнение 2. Модель Харрода – Домара воспроизводства ЧВП имеет вид:
Y (t) B dYdt(t) kY (t) A(t), или sY (t) B dYdt(t) A(t)
или
dY (t) dt
где k – постоянная доля или норма непроизводственного потребления, предельная склонность к потреблению, s 1 k – постоянная доля или норма производственного накопления, предельная склонность к сбережению, A(t) – автономные (внешние) инвестиции, Y (t) – ЧВП.
49
Найти Y (t) |
в |
следующих |
случаях: |
A(t) 0, |
A(t) A(0)δ(t), |
A(t) A(0) const, |
A(t) A(0)er t , |
A(t) A(0)(1 sin(t)), |
A(t) At A(0). |
||
|
|
|
|
|
1 |
Взять те же значения |
B , что и в предыдущем задании, и значения s |
||||
в зависимости от номера в группе: s 0,01; 0,02; |
; 0,36. |
|
|||
Упражнение 3. Рассмотрим линейную односекторную модель выпуска валового внутреннего продукта (ВВП) с учетом выбытия (амортизации) с инерционным запаздыванием фондообразования:
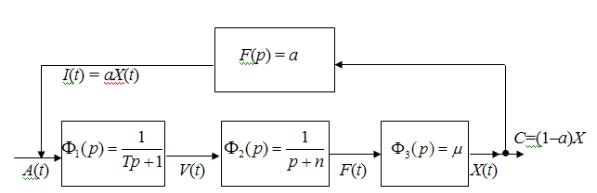
Обозначения: X(t) – ВВП, A(t) – внешние, автономные инвестиции, I(t) – собственные инвестиции, V(t) – реальные инвестиции в производство, F(t) – основные производственные фонды (ОПФ), C(t) – конечное, непроизводственное потребление, μ – средняя капиталоотдача, а – средний норматив отчислений на капитальные вложения, n – средняя норма амортизации ОПФ, Т – лаг фондообразования. Тогда справедливы равенства:
X (p) Wc (p)A(p), Wc (p) |
|
|
|
1(p) 2(p) 3 |
(p) |
, |
||||
1 |
1(p) 2(p) 3(t)F(p) |
|||||||||
|
|
|
|
|||||||
Wc (p) |
|
|
|
|
μ |
|
, |
|
|
|
Tp2 |
(Tn 1)p n aμ |
|
|
|||||||
|
|
|
|
|||||||
модель имеет вид
T d 2X (Tn 1)dX (n aμ)X μA(t). dt2 dt
Рассмотреть ситуации разных n , a и μ: n aμ, n aμ, n aμ.
50
