1 Вопрос. Комплексные числа. Определение комплексного числа. Свойства операций над комплексными числами.

Комплексным числом  называется число вида , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью () комплексного числа , число  называется мнимой частью () комплексного числа .

Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой  принято обозначать множество действительных чисел.Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой. Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

Сложение комплексных чисел

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

z₁ + z₂ = (a₁ + a₂) + i*(b₁ + b₂).

Для комплексных чисел справедливо правило первого класса: z₁ + z₂ = z₂ + z₁ – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

z₁ + z₂ = (a₁ – a₂) + i*(b₁ – b₂)

Умножение комплексных чисел

Основное равенство комплексных чисел:

Произведение комплексных чисел:

z₁ * z₂ = (a₁ + i*b₁)*(a₂ + i*b₂) = a₁*a₂ + a₁*i*b₂ + a₂*i*b₁ + i²*b₁*b₂ = a₁*a₂ - b₁*b₂ +i*(a₁*b₂ +a₂*b₁).

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

Деление комплексных чисел

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

2 Вопрос. Комплексная плоскость. Модуль и аргументы комплексных чисел

Каждому комплексному числу z = a + i*b  можно сопоставить точку с координатами (a;b) , и наоборот, каждой точке с координатами (c;d) можно сопоставить комплексное число w = c + i*d . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.

Однако чаще комплексные числа изображают в виде вектора с началом в точке О , а именно, комплексное число z = a + i*b изображается радиус-вектором точки с координатами (a;b) . В этом случае изображение комплексных чисел из предыдущего примера будет таким:

Изображением суммы двух комплексных чисел , является вектор, равный сумме векторов, изображающих числа и . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие.

Пусть комплексное число z = a + i*b  изображается радиус-вектором. Тогда длина этого вектора называется модулем числа z и обозначается |z| .

Угол, образованный радиус-вектором числа с осью, называетсяаргументом числа и обозначаетсяarg z . Аргумент числа определяется не однозначно, а с точностью до числа, кратного . Однако, обычно аргумент указывают в диапазоне от 0 доили в диапазоне от  -до. Кроме того у числааргумент не определен.

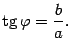
С помощью этого соотношения можно находить аргумент комплексного числа:

или

(17.7)

причем первая формула действует, если изображение числа находится в первой или четвертой четверти, а вторая, если -- во второй или третьей. Если , то комплексное число изображается вектором на оси Oy и его аргумент равен /2или  3*/2.

Получим еще одну полезную формулу. Пусть z = a + i*b . Тогда ,

или .