6. Гироскоп и гироскопические явления

Цель работы: усвоение знаний по разделу «Движение гироскопа», приобретение практических навыков определения момента инерции твердых тел.

Оборудование

Общий вид экспериментальной установки представлен на рисунке 1. Основными элементами установки являются:

1- гироскоп 3-х осевой;

2- фотоэлектрический датчик;

3- секундомер;

4- пластина с гирей;

5- нить;

6- подвижный противовес;

7- стержень;

8– держатель.

6 1 2

8

Рис. 1. Общий вид установки

39

6.1. Задание для работы

1.Определить момент инерции гироскопа измерением углового ускорения.

2.Определить момент инерции гироскопа измерением периода вращения и периода прецессии.

6.2. Методика эксперимента

6.2.1. Краткие теоретические сведения

Гироскопом называется тело, вращающееся вокруг своей оси симметрии с высокой угловой скоростью.

r*

z

Рис. 2. Схема движения гироскопа

В данной работе гироскоп представляет собой диск, насаженный на стержень АВ, который совпадает с осью вращения. Положение центра масс гироскопа регулируется подвижным противовесом 6 (рис. 1 и 2). Гироскоп устроен так, что он может вращаться не только вокруг своей оси симметрии (ось ОХ), но также вокруг вертикальной и горизонтальной осей ОY и ОZ.

3.Определение момента инерции гироскопа измерением углового ускорения

1

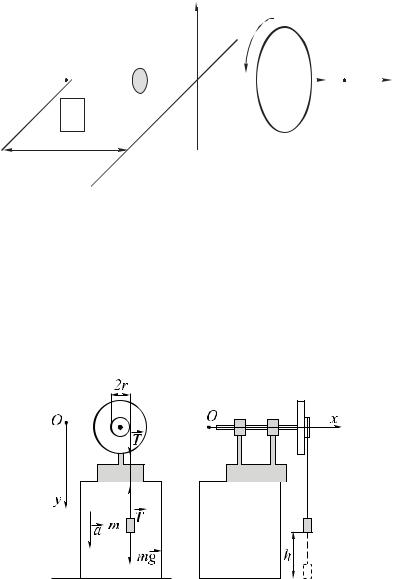
Рис. 3. Схема экспериментальной установки для определения момента инерции гироскопа

Одним из известных методов определения момента инерции гироскопа является метод, основанный на вращении гироскопа вокруг закрепленной оси под действием постоянной силы. Такое вращение можно осуществить с помощью нити, намотанной на гироскоп, к свободному концу которой прикреплен груз массой m (рис. 3).

40

Движение гироскопа описывается уравнением динамики вращательного движения твердого тела:

где M − результирующий вращательный момент, I – момент инерции гироскопа, ε − его угловое ускорение, ω − его угловая скорость.

Силой, вызывающей вращение гироскопа, является сила натяжения нити Т (рис. 3), поэтому М =[r T ] (r – радиус барабана). Уравнение (1) в проекции на ось ОХ имеет

Поступательное движение груза описывается вторым законом Ньютона

T1 + mg = ma ,

где g – ускорение свободного падения, а – ускорение груза. В проекции на ось OY

4. Определение момента инерции гироскопа измерением периода вращения и периода прецессии

Более распространенным методом определения момента инерции гироскопа является метод, основанный на свободном движении гироскопа с закрепленным центром масс.

Основное свойство свободного гироскопа с закрепленным центром масс, которое объясняет его поведение под действием сил, состоит в том, что вектор момента

импульса L совпадает с вектором угловой скорости ω , направленным вдоль оси ОХ,

Поэтому о движении оси гироскопа можно судить по изменению направления вектора L , описываемого уравнением моментов:

dLdt = M .

Зная результирующий момент сил M , всегда можно определить направление движения оси по соотношению dL = Mdt .

Нарушим равновесие гироскопа с помощью дополнительного груза массой m* .

41

ddtL =[ r * × m* g ]

или в проекции на ось OZ

Если бы гироскоп не находился в быстром вращении, то под действием дополнительной силы m* g его ось симметрии, которая совпадает с АВ, должна была бы отклониться от горизонтального положения. Но наличие вращения полностью изменяет результат действия силы. Поскольку вектор изменения момента импульса dL

сонаправлен с моментом силы М , то конец оси гироскопа начинает двигаться в горизонтальной плоскости, повернувшись за время dt на угол dα (рис. 4).

Рис. 4. Прецессия горизонтальной оси гироскопа

Момент импульса гироскопа, получив приращение dL за время dt , в следующий момент времени t + dt будет равен

L1 = L + dL .

В результате ось гироскопа будет вращаться с некоторой угловой скоростью ωпр . Такое

движение называется прецессией. Если при этом сила, вызывающая прецессию сохраняет свое значение, то движение оси происходит с постоянной угловой скоростью

ωпр :

ωпр = ddtα .

Из треугольника ОВВ1 (рис. 4) L dα = dL ,поэтому

Зная связь между угловой скоростью вращения гироскопа вокруг своей оси ω и

42