4.3.Теплоемкость в политропном проессе.

Из общей формулы теплоёмкости однородных систем имеем:

(62)

Была поучена:

(64)

Здесь Cn- массовая теплоемкость в политропном процессе .

Так как газ в политропном процессе полагается идеальным, то

Подставим в уравнение (64)

подставим в уравнение

_{Здесь по уравнению Майера R=C}p_-Cv _,

(122)

(122)- массовая теплоемкость в политропном процессе.

Так как k>1, то при 1<n<k – имеем c_n<0. С точки зрения физики это трудно объяснимо, поэтому продолжим процесс вычисления с этим значением:

В силу универсальности уравнения можно формально рассмотреть изопроцессы как частные случаи политропного процесса:

1. При n=0 →p=const, n_p = 0

2. При n=0 → pv=const (T=const), n_T = 1

3. При n=k →S=const(pv^k=const), n_A = k

4. При n=(v=const), n_v = .

Изобразим процессы на pv-диаграмме, для кривых возьмём общую точку:

пунктирной линией изображены процессы не относящиеся к простейшим.

4.4.Работа, теплота и внутренняя энергия в политропном процессе.

Абсолютная работа термодеформационной системы определяется:

Для того чтобы взять интеграл надо знать связь между P и v. Найдем связь из уравнения политропы:

pvⁿ=const,

(123)

Получим ещё несколько формул для вычисления работы. Преобразуем формулу (123):

Окончательно:

(124)

Выразим отношение из уравнения политропы

Выразим отношение температур из уравнения:

(125)

Или (126) (125), (126) широко используются в теории газовых турбин, теории компрессоров, газовой динамике

В политропном процессе газ считается идеальным, а для идеального газа , и для любого процесса, в том числе и для политропного.

Теплота в политропном процессе определяется:

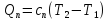
После подстановки

dQ = T dS

dQ = c dT

c dT = T dS => dS = =>dS_n = c_n =, проинтегрировав, получим

.

Если за начало отсчета S взять нормальные физические условия, то можно получить формулу для энтропии:

.

Получим ещё несколько формул:

=> =>

, при нормальных физических условиях получим .

Исследование изопроцессов. Работа, теплота и внутренняя энергия в изопроцессах.

1. v = const, =>A_v = 0, ,

(Q = U + A => Q_v = U_v)

2. T = const, , n_T = 1, p₁v₁ = p₂v₂ = RT = const

, ,,

, ,,U_T = 0

U = c_v (T₂ – T₁) = 0,

Q = U + A => Q_T = A_T

3. p = const, , n_p = 0

Получим ещё одну формулу для расчёта теплоты. 1-ое начало термодинамики в энтальпийной форме

dU = TdS – p dv = dQ – p dv,

dU = dQ – p dv – v dp + v dp = dQ – d(pv) + v dp,

dQ = dU + d(pv) – v dp = d(U+pv) – v dp,

dQ = dI – v dp - 1-ое начало термодинамики в энтальпийной форме.

Из этого уравнения для изобарного процесса получим:

dQ_p = dI => Q_p = I₂ – I₁.

Таким образом, в изобарном процессе теплота может быть вычислена по двум формулам:

и ,.

.

4. Адиабатный dQ=0, S=const

, n_s = k,

; ;

Из 1-ого начала термодинамики следует:

dQ = dU + dA, dA_S = - dU_S, A_S = - U_S