6. Формулировка Теоремы существования единственности решений задчи Коши.

Частное и общее решение Ду, Ду 1 порядка, его геометрический смысл .

Поле направлений Изоклины. Особые точки, особые решения ДУ с разделяющимися переменными.

Если функция f(x,y0,y1…yn-1) в открытой области R^n+1 непрерывна и обладает в ней непрерывностью пусть

Дифференциа́льное уравне́ние — уравнение, связывающее значениепроизводнойфункциис самой функцией, значениями независимой переменной, числами (параметрами).

Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него.

Решением (интегралом) дифференциального уравнения порядка n называется функцияy(x), имеющая на некотором интервале(a, b) производные до порядкаn включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием.

Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, После определения вида указанных постоянных и неопределенных функций решения становятся частными.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений(обыкновенныхис частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемымначальным условиям(начальным данным).

Говорят, что задача Коши имеет единственное решение, если она имеет решение и никакое другое решение не отвечаетинтегральной кривой, которая в сколь угодно малой выколотой окрестности точкиимеетполе направлений, совпадающее с полем направлений. Точказадаёт начальные условия.

Каательная к функции, скорость-производная производная от координаты по времени есть скорость

ИЗОКЛИНА

обыкновенного дифференциального уравнения 1-го порядка

- множествоточек плоскостих, у, в к-рых наклон направлений поля, определяемого уравнением (*), один и тот же. Если к- произвольное действительное число, то k-изоклина уравнения (*) есть множество

Точки пересечения двух или нескольких изоклин могут быть особыми точками дифференциального уравнения (1), т.е. такими точками, в которых правая часть уравнения (1) не определена.

7.Ду 1 порядка, однородные и сводящиеся к ним, ду в полных дифференциалах.

8.Линейные ДУ 1-го порядка, уравнения Бернулли.

9.ДУ не разрешенные относительно производной, уравнения разрешенные относительно одной из переменных. Уравнение Лагранжа и Клеро.

Лагранж и клеро далее.

10. ДУ не разрешимые относительно производной. Уравнения не

имеющие одной из перменных.

.

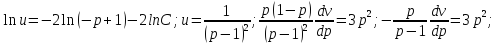
11.ДУ. Допускающие понижение порядка.

F(x,y,y'...)=0;F(x,y0,y1...)=0; 0 применим параметрический метод.

x=,y=,y'=g(U,V); dy=y'dx==g(U,V)dx; dx=dU+dV;dy=dU+dV

dy=g(U,V); F(y,y',y''...)=0 ;y'=p,y''=p; F1(y,p, p...)=0 p=

dy/dx=ДУ первого порядка.=

12.Нормальная система ДУ, координатная и векторная запись. Основные понятия, задача Коши, формулировка теоремы существования и единственности решений.

13. Линейные ДУ. и их нормальные системы, матричная запись систем, основные понятия, существования решений.

14 Линейный дифференциальный оператор. Свойства решений ЛДУ и их систем.

Cвойство ЛДУ

1)Всякая лин. Комбинация решений ЛОДУ является решением этого уравнения или системы.

Док-во.

2) разность любых 2х решений ЛДУ или СЛДУ является реш соотвующ однород ур или системы.

Док-во.

3) Сумма любого реш ЛДУ и любого реш соотв однородного урав-ния или системы, является реш данного уравнения или системы.

4)Если

Док-во. (4)-тождестств.

Т.е комб удволетворяет (5)это утверждение называется принцип суперпозиции

15. Однородные ЛДУ и ЛОДУ и их системы. Пространсто их решений и его связь с арифметическим пространством, размерность. ФСР. Фундаметральная матрица.

; собственные и присоединенные векторы – корневые векторы

P=1

Сравним полученные формулы с (2)

.

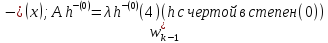
(спутано к и n сам знаю что где. См выше)

Сумма кратная собственн числам равна порядку матрицы

)=

(непонятно где n, а где k) (5) –является решением в сист 1

А в т 0 они образуют корневые векторы

А в корн. Векторы сист. л/нез.; а из л/нез в точках=>л/нез на всем промежутке, значит 5 л/нез.

16. Теоремы о структуре общего решения ЛДУ и систем ЛДУ.

Определение 1.

Система функций лин. Незваисима, если никакое их нетривиальная комбинация ЛК≢0 и линейно зависим в противном случае.

Система фектор функций называется Лин независимой в промежутке, если никкая Нетривиальная ЛК≢0 в этом промежутке.

Система вектор – функций Л зависима в промежутке, Л Зависима в каждой точке.

Следствие. Если сист вектор. Функций л/независима хотя бы а 1 точке промежутка, то она л/независима и в промежутке.

Замечание Обратное для произвольных вектор функций неверно(касательно самого утверждения)

Теорема 1.

Множество решений ЛОДУ или СЛОДУ, есть линейное пространство.

Док-во.

Л.Операция, т е сложение и уножение на число вводятся обыч образом, как операции над функциями и вектор-функциями. Т к Диф(дифференцирование?) вектор-функция выполняется покоординатно,и лин. оператор так же, а линейный. опрер. над скаляр. функциями выполняются как операции над их числ. значениями, то эта операция обладает всеми свойствами сложения и умножения чисел. => для них выполняется все аксиомы ЛП(линейного пространства)

Теорема 2.

пространство U – изоморфно

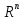
Док-во.

взаимооднозначное соответсвие. и при уножении на число начальный вектор умножают на число. т е

Следствие 1

Пространство решений н-мерно, система ДУ н-мерно

Следствие 2

Всякое ЛОДУ с неопред коофицентами имеет Фундаметальную систему решений

Следствие 3

Система решений СОДУ л/независима в промежутке, т. и т.т., когда она л/независима в точке этого промежутка.

Следствие 4

Теорема 3 Общее решение СОДУ есть ЛК ФСР с произволь. постоянными коофиуентами.

Док-во

пусть

1. всякое ЛОДУ с непрерывными коофицентами имеент ФСР

2.Общее решение ЛОДУ есть ЛК его ФСР с произвольными коофицентами.

Т4

Док-во

пусть частное решение;i=– ФСР (8)тогда по 2му свойству разностьур 7 иy0(x)- есть решение 8;

(при соответств)

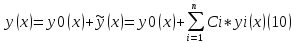
(10)-содержит в себе все части решения уравнения (7) y(x)-при любых Ci является решенем (8)по свойству 3 y(x)=y0(x)+(x) – решение 7; 10 при любых Ci –общее решение 7; y(x)- общ. решение 8ж так что обще реш 7, есть частное решение 8.