3.2.1. Подстановки Эйлера.

Интегралы вида могут быть приведены к интегралу от рациональной функции с помощью подстановок Эйлера.

Первая подстановка Эйлера применима, если

Из указанной подстановки имеем ,.

Пример 43. =

Замечание. При рационализация интеграла может быть достигнута с помощью подстановки, где комбинация знаков произвольна.

Вторая подстановка Эйлераприменима при Из указанной подстановки получаем:

Пример 44 (см.пример 43 ).

Третья подстановка Эйлера применима всякий раз, когда квадратный трехчлен имеет действительные корни (- любое число, отличное от нуля).

Пусть и корни квадратного трехчлена . Тогда

из подстановки имеем

Пример 45. J=

Подкоренное выражение положительно при 1<<2. Тогда, полагая

, имеем

J=

3.2.2. Интегрирование выражений вида .

Указанные выражения являются частными случаями выражения . Для интегрирования первого из этих выражений может быть применен метод неопределенных коэффициентов:

=,

где коэффициенты многочлена и числоопределяют следующим образом.

Обе части последнего равенства дифференцируют по и результат умножают на:=,

Далее сравнивают коэффициенты при одинаковых степенях .

Пример 46. =

Умножаем обе части равенства на.

=.

Приравниваем коэффициенты при одинаковых степенях

=

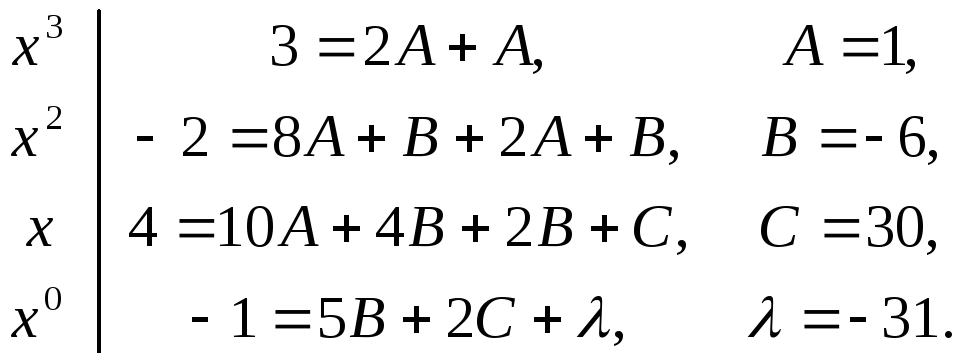
Замечание. Вычисление интеграла

умножением и делением на сводится к вычислению интеграла.

Пример 47.

=+

Замечание. Вычисление интеграла заменойсводится к

вычислению интеграла

Пример 48.

Неопределенные коэффициенты инаходим из равенства

Сравнивая коэффициенты при одинаковых степенях , имеем

3.2.3.Тригонометрические подстановки приводят интегралы

к интегралам вида .

Интегралы вида

Замена , тогда

Пример 49.

Интегралы вида.Замена

Пример 50.

Интегралы вида

Замена

Пример 51.

Замечание.

Подстановка приводит интеграл

к одному из следующих ,

Замечание. Если в выражении, содержащем указанные радикалы, присутствует в нечетной степени, то вполне эффективной может оказаться заменаили

Пример 52.

3. Биномиальные дифференциалы т.е. дифференциалы

вида гдеи- постоянные, отличные от 0, а- рациональные числа.

Первообразная функции является элементарной функцией в следующих трех случаях:

1) -целое число (замена где-общий знаменатель дробейи

2)-целое число (заменагде-знаменатель

дроби

3)-целое число (заменагде

- знаменатель дроби

Пример 53.

Метод нахождения последнего интеграла подробно описан в разделе “ ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ“.

Пример 54.

Пример 55.

Оглавление введение 3 основные свойства неопределенного интеграла 3

ТАБЛИЦА ИНТЕГРАЛОВ 4

ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 4

1. Непосредственное интегрирование 4

2. Метод подведения под знак дифференциала 5

3. Замена переменной ( метод подстановки) 7

3.1.Интеграл вида 7

3.2.Интегралы вида ,8

3.3. Интегралы вида8

3.4. Интегралы вида9

4. Интегрирование по частям 10

КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ 13

1.Дробно-рациональные функции 13

2. Тригонометрические функции 19

2.1. Итегралы вида 19

2.2. Интегралы вида

20

2.3. Интегралы вида 20

3. Некоторые иррациональные функции 22

3.1. Интегрирование рациональной функции вида 22

3.2. Интегрирование рациональной функции вида 24