Способ частных значений. Умножаем тождество (*) на и приходим к равенству. Придаваяподходящие конкретные значения, получаем систему уравнений для нахождения коэффициентов разложения.

Замечание. Иногда для определения коэффициентов разложения вышеуказанные способы комбинируют..

После разложения правильной дробно-рациональной функции её интегрирование сводится к интегрированию простейших рациональных дробей:

подстановкой

сводится к линейной комбинации интегралов

подстановкой сводится к линейной комбинации интегралов

и .

Первый из этих интегралов ( см. пример 6).

Второй интеграл можно вычислить с помощью следующей рекуррентной формулы:

.

Пример 29..

Подинтегральная функция является правильной рациональной дробью, поэтому она представима в виде суммы простейших рациональных дробей:

. Умножим обе части последнего равенства на и получим равенство

.

Принимая и сравнивая коэффициенты прии свободном члене, имеем:

Пример 30. .

Подинтегральная функция – правильная рациональная дробь – представима в виде суммы простейших рациональных дробей:

Умножая обе части на , имеем:

=

Пример 31.

Разложение на простейшие дроби часто требует громоздких выкладок, поэтому не следует пренебрегать возможностью упростить вычисления с помощью алгебраических преобразований, замены переменной и других известных методов.

Пример 32.

Пример 33.

2. Тригонометрические функции

2.1. Интегралы вида гдеи-целые числа, вычисляются с помощью искусственных преобразований или применением формул понижения степени. Если хотя бы одно из чиселилинечетное, то данный интеграл заменойилиприводится к интегралу от рациональной функции (см. 3.4). Еслиичетные числа, то возможно применение следующих формул:

Пример 34.

Пример 35.

2.2. Интегралы вида находятся с помощью следующих формул:

Пример 36.

2.3. Интегралы вида где- рациональная функция, в общем случае приводятся к интегралам от рациональных функций с помощьюуниверсальной подстановки

Замечание. Если выполнено равенство или,

то целесообразно применить подстановку или

Замечание. Если выполнено равенство

,то целесообразно применить подстановку

.

Пример 37.

Пример 38.

Пример 39.

Замечание.Иногда удобно разделить числитель и знаменатель на .

Пример 40 ( см. пример 39 ):

Замечание. Не следует догматически применять приведенные выше правила. Рекомендуемая замена приводит интеграл к довольно сложному интегралу, тогда как универсальная подстановкапозволяет вычислить его легко и просто:

Этот же интеграл можно найти и другим способом:

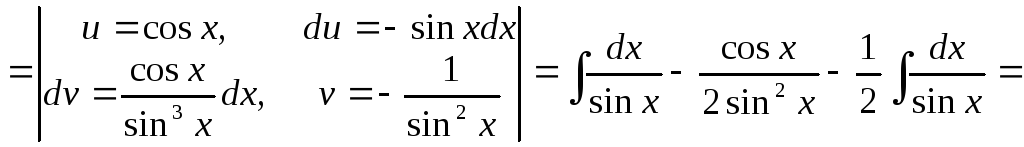
3. Некоторые иррациональные функции

3.1. Интегрирование рациональной функции вида

Замена

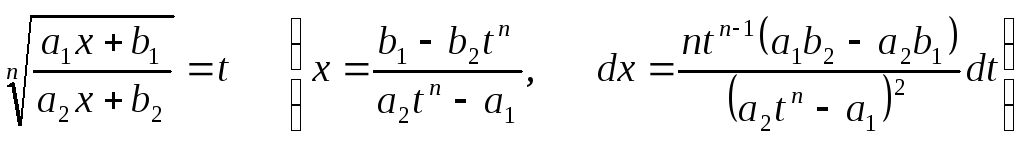
приводит к интегралу от рациональной функции переменной

Пример 41.

.

.

Замечание. Интеграл вида является частным случаем интеграла

Замена приводит

к интегралу от рациональной функции переменной

Пример 42.

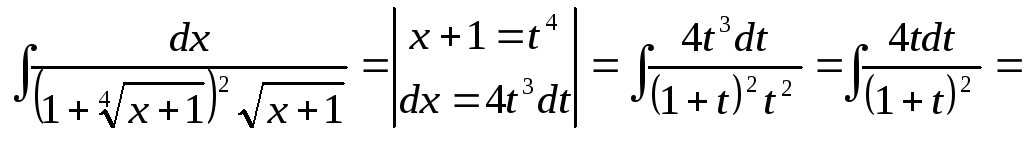
3.2. Интегрирование рациональной функции вида .