3.3. Интегралы вида

Пример 14.

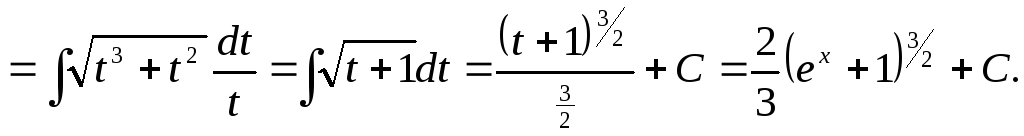
3.4. Интегралы видагдеи-целые числа, заменойилиприводится к интегралу от рациональной функции относительно переменной

Пример 15.

Рассмотрим еще несколько примеров.

Пример 16.

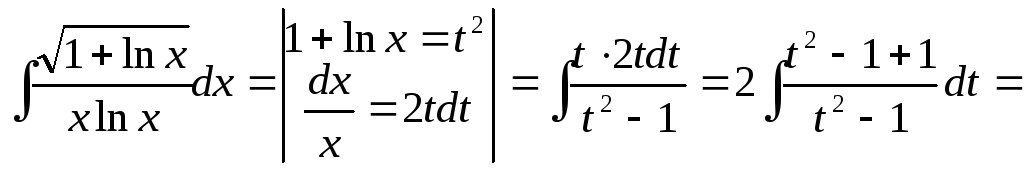
Пример17.

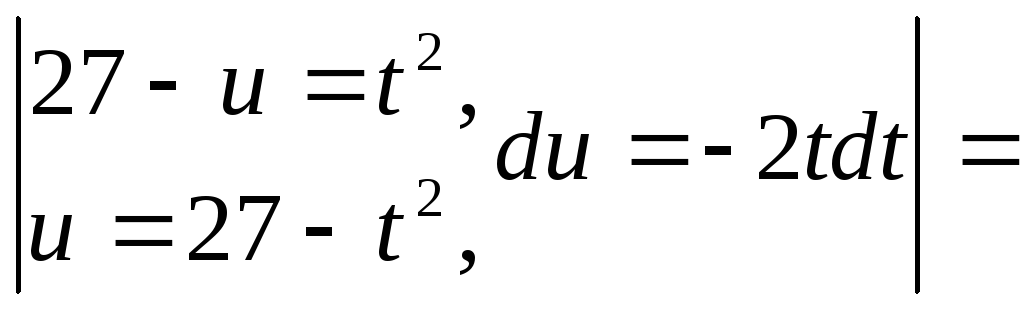
Пример 18.

=

Пример 19.

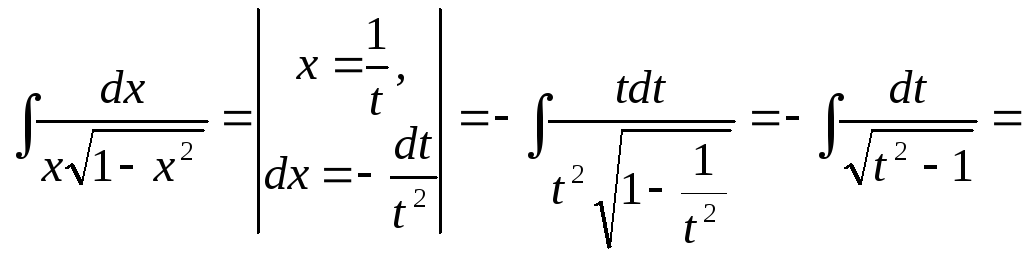
Пример 20.

Более сложные замены будут рассмотрены далее.

3. Интегрирование по частям

Если и непрерывно дифференцируемые функции, то справедлива формула

Суть применения этого метода состоит в том, что при удачном выборе ивычисление интегралаоказывается проще, чемМетод применяется, если под знаком интеграла стоит произведение“ разнородных “ функций, например, и,и,и, а также, если подинтегральное выражение содержит логарифмическую или обратные тригонометрические функции и некоторые другие функции.

Пример 21.

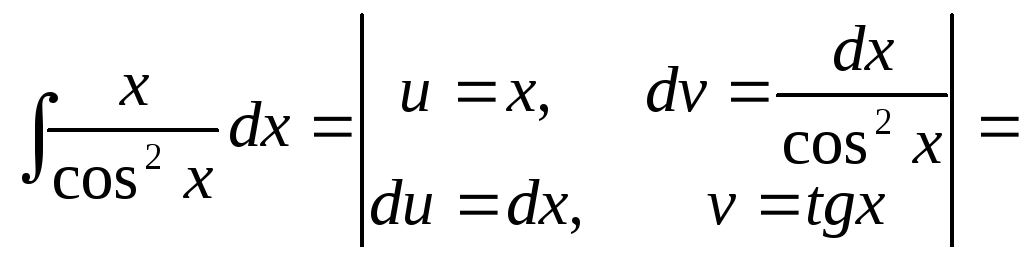
Пример 22.

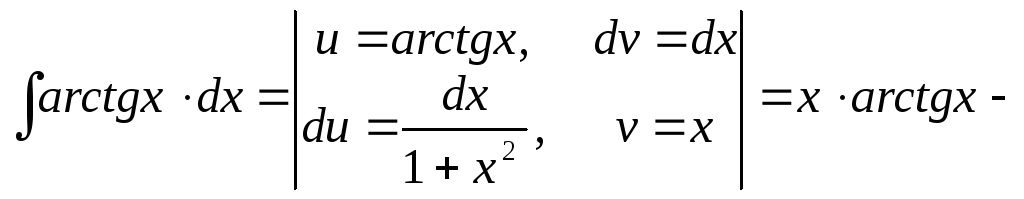
Пример 23.

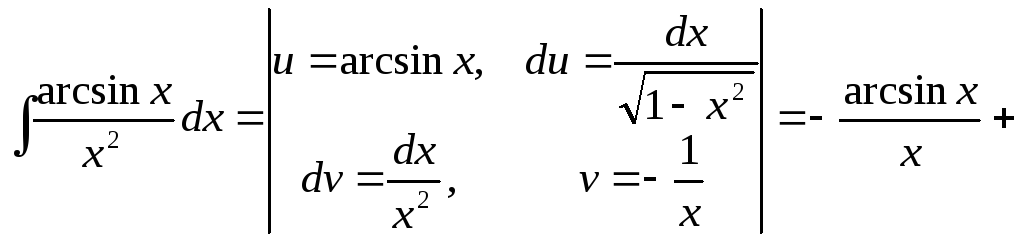
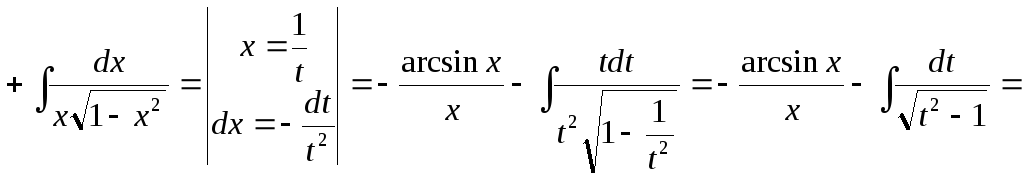
(см. пример 19).

Пример 24.

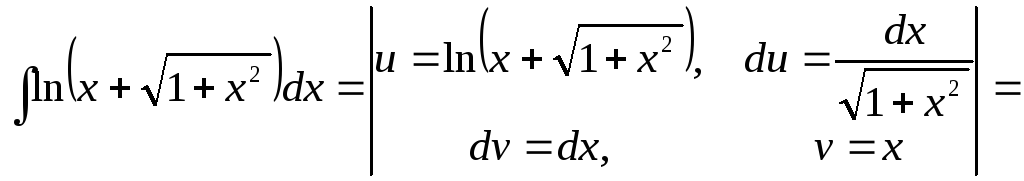
Пример 25. ( Возвратный интеграл ).

откуда

Примечание. Интегралы типа иудобно вычислять с помощью неопределенных коэффициентов. Пример 26.

Дифференцируем это равенство и приравниваем коэффициенты при функциях и.

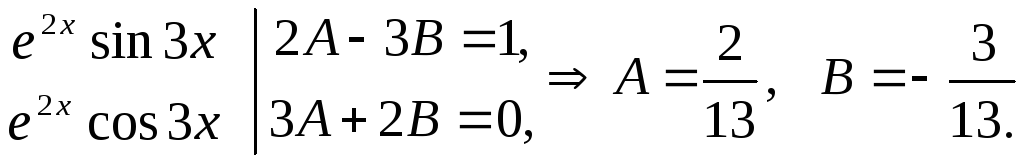
Следовательно,

Пример 27.

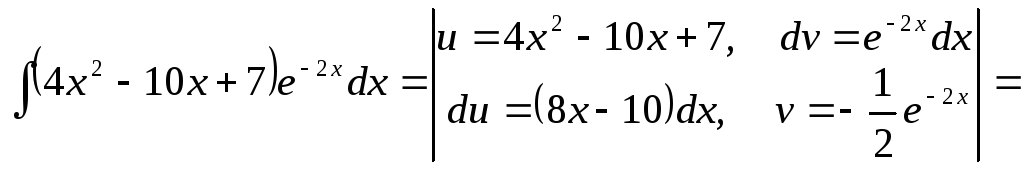
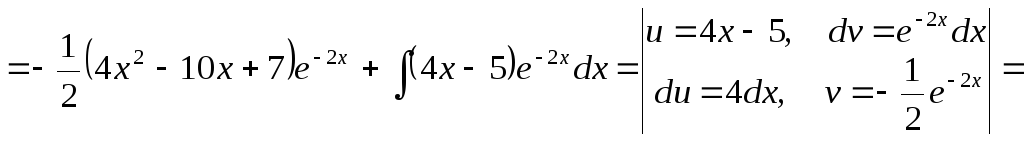
Примечание. При решении примеров такого типа можно также применить метод неопределенных коэффициентов.

Пример 28.

.

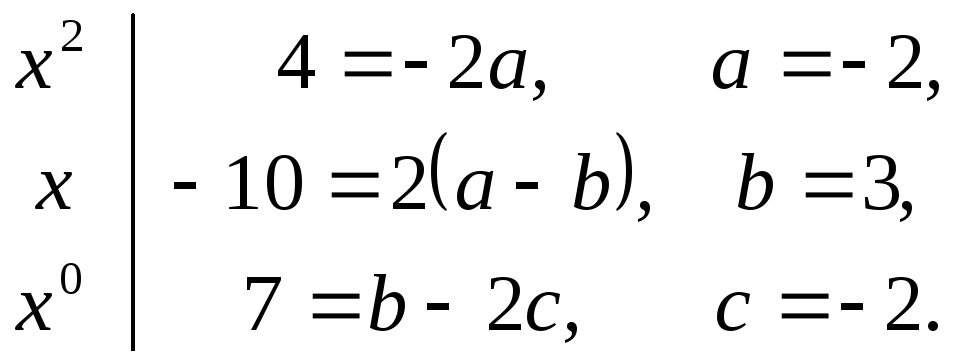
Основные классы интегрируемых функций

1.Дробно-рациональные функции

Дробь гдеи- многочлены, называетсядробно-рациональной функцией (рациональной дробью).

Дробь правильная, если и неправильная при

В случае интегрирования неправильной дроби необходимо выделить целую часть этой дроби .При этом вычисление интеграла сводится к интегрированию многочлена и правильной дроби.

Рациональные дроби вида

,

называются простейшими рациональными дробями.

Интегрирование правильной рациональной дроби сводится к интегрированию суммы простейших рациональных дробей.

Имеют место следующие утверждения.

Утверждение 1.1.

Если правильная дробно-рациональная функция, гдето указанная функция может быть представлена в следующем виде:

где последнее слагаемое вновь правильная дробно- рацио-нальная функция.

Утверждение 1.2.

Если 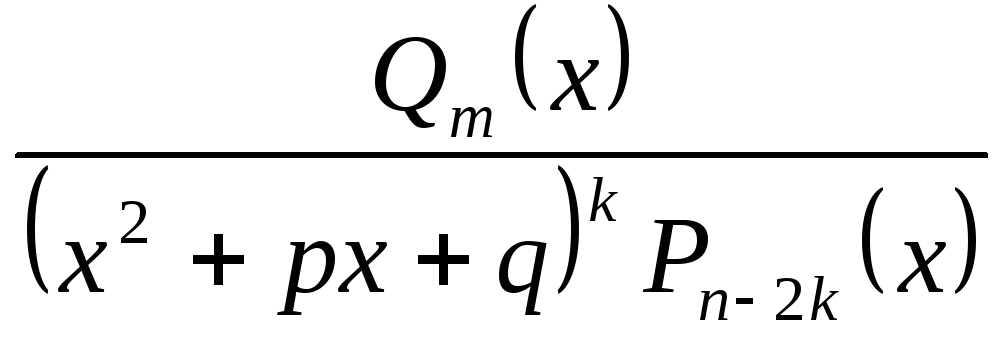правильная дробно-рациональная функция, то она может быть представлена в виде суммы:

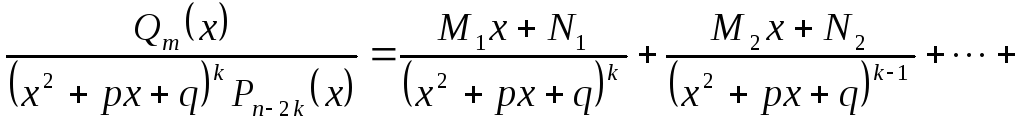
где последнее слагаемое снова пра-вильная дробно-рациональная функция.

Утверждение 1.3.

Любая дробно-рациональная функция может быть представлена в виде суммы многочлена и простейших рациональных дробей.

Утверждение 1.4

Если

то правильную дробно-рациональную функцию можно представить в виде суммы простейших рациональных дробей:

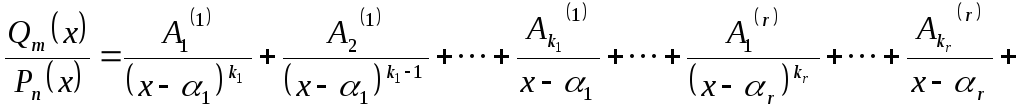
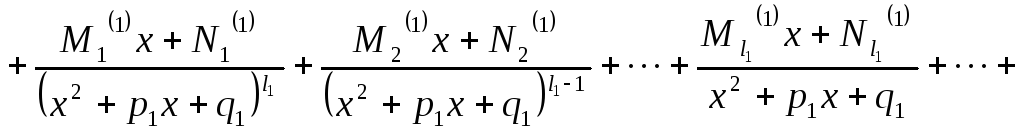
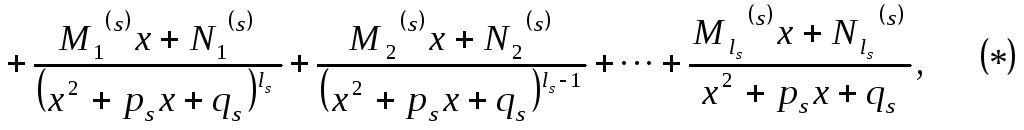причем сумма содержит столько слагаемых,сколько множителей, с учетом их кратности, в разложении многочлена

Для нахождения коэффициентов разложения

могут быть использованы следующие способы.

Способ соответствующих коэффициентов. Умножаем тождество (*) на и получаем равенство многочленов.После этого , приравнивая коэффициенты при соответствующих степенях, получаем систему алгебраических уравнений для определения коэффициентов разложения.