Введение

Функция ,определенная и непрерывная на том же множестве, что и функция, называетсяпервообразной функции , если

Очевидно, что если -первообразная функции, то+С, где С-произвольная константа, также является первообразной.

Имеет место следующее утверждение: две первообразные одной и той же функции отличаются друг от друга только на некоторую постоянную.

Следовательно, если - первообразная функции, то множество всех первообразных функцииимеет вид+С.

Множество всех первообразных функции называетсянеопределенным интегралом от функции и обозначается

Обычно пишутгде-любая перво-образная функции. Интеграл может быть записан в любом из видов:

Отсюда видно, что операция нахождения интеграла от данной функции, называемая интегрированием, является действием, обратным дифференцированию.

Основные свойства неопределенного интеграла

, если перво-образные функций исуществуют.

ТАБЛИЦА ИНТЕГРАЛОВ

1..

2..

3..

4..

5..

6..

7..

8..

9..

10..

11..

12..

13..

14..

15..

16..

17..

18..

.

ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

1. Непосредственное интегрирование

Нахождение неопределенного интеграла состоит в основном в преобразовании подинтегрального выражениятаким образом, чтобы получить табличные интегралы.

В некоторых случаях удобно представить подинтегральную функцию в виде суммы двух слагаемых и вычислять сумму неопределенных интегралов от слагаемых ( Метод разложения:

если ).

Пример 1.

Пример 2.

2.Метод подведения под знак дифференциала

( метод введения нового аргумента)

Таблица интегралов справедлива независимо от того, является ли переменная интегрирования независимой переменной или функцией ( инвариантность формул интегрирования).

Если

где функция непрерывна вместе со своей производной.

Преобразование подинтегрального выражения к такому виду называется подведением под знак дифференциала.

Таким способом можно найти многие интегралы, не прибегая к более сложным методам.

Так как , то

Пример 3.

Пример 4.

Пример 5.

Пример 6.

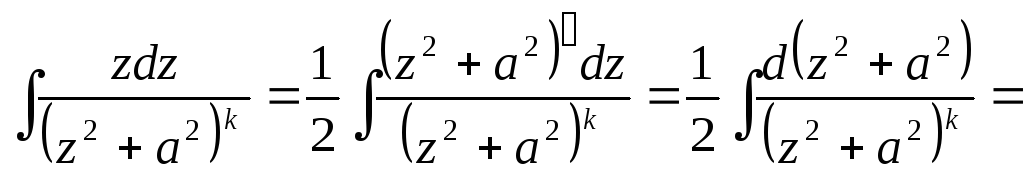
Пример 7.

Пример 8.

=

Пример 9.

Пример 10.

2. Замена переменной ( метод подстановки )

Замена переменной или метод подстановки является одним из основных методов интегрирования. Нередко приходится прибегать к подстановке в процессе вычисления интегралов другими методами.

Пусть функция непрерывна, функции,взаимно обратны и непрерывно дифференцируемы, тогда

Функция подбирается таким образом, чтобы подинтегральное выражение приняло более удобный для интегрирования вид.

При применении подстановки главная трудность состоит в том, чтобы получить подинтегральную функцию , первообразная которой известна.

Излишне упоминать о том, что не каждая подстановка ведет к упрощению. Когда подстановка выгодна и какую именно подстановку следует применить и рассматривается далее.

3.1.Интеграл вида При вычислении интегралов этого вида целесообразна замена

Интеграл вида заменойприводится к интегралу

Пример 11.

=

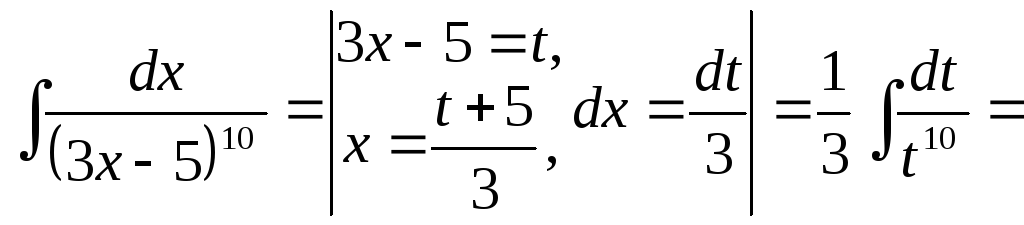
Пример 12.

3.2.Интегралы вида ,

заменой приводят к интегралам

Вычисление этих интегралов в зависимости от знака числа сводится к вычислению интегралов вида

Каждый из них представляет собой сумму двух интегралов, один из которых табличный, а другой вычисляется подведением под знак дифференциала ( см. примеры 4,5 ).

Замечание. В частном случае

(См. также пример 9).

Пример 13.