5.3. Смешанное произведение векторов.

Определение и геометрический смысл смешанного произведения.

Если вектор умножить векторно наи полученный векторумножить скалярно на вектор, то число, полученное в результате этих умножений, называетсясмешанным произведением векторов .

Определение. Число, равное , называютсмешанным произведением векторов .

Смешанное произведение векторов обозначаетсяили.

На векторах, приложенных к общему началу, можно построить параллелепипед (рис. 2.21). Если векторыобразуют правую тройку, то, где - площадь параллелограмма,Рис. 2.21 построенного на векторах и, авысота параллелепипеда, построенного на векторах.

Итак, если векторы образуют правую тройку, то смешанное произведение этих векторов численно равно объёму параллелепипеда, построенного на этих векторах.

Если векторы образуют левую тройку, то угол между векторамиитупой и, при этомравен объёму параллелепипеда, построенного на этих векторах.

Смешанное произведение в координатной форме.

Пусть ,и. Тогда

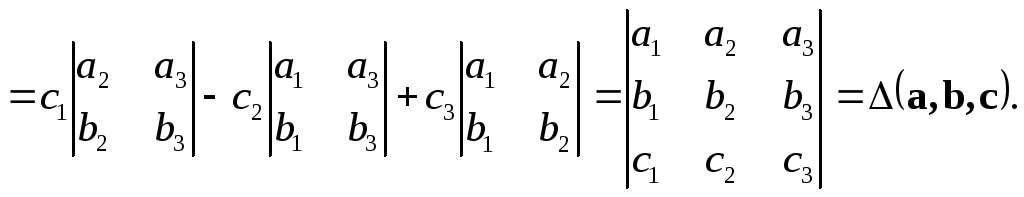Итак, смешанное произведение векторов в координатной форме равно определителю, построенному на векторах.

Свойства смешанного произведения.

Так как , то свойства смешанного произведения могут быть получены из свойств скалярного произведения и свойств определителя.

Свойства смешанного произведения:

а) .

Знаки векторного и скалярного произведений можно переставить местами, но при этом необходимо вначале перемножить соответствующие сомножители векторно.

►Действительно, пользуясь переместительным законом для скалярного произведения и свойствами определителя, имеем ◄

б) .

Два сомножителя смешанного произведения можно поменять местами, при этом абсолютное значение смешанного произведения не меняется, а его знак меняется на противоположный.

Докажем, что .

►Действительно, ◄

в) Смешанное произведение векторов равно нулю тогда и только тогда, когда векторы компланарны.

Доказательство этого свойства следует из геометрического смысла смешанного произведения.

Применение смешанного произведения.

1. С помощью смешанного произведения можно вычислить объём параллелепипеда, построенного на векторах .

.

Это следует из геометрического смысла смешанного произведения.

Замечание. Объем тетраэдра, построенного на векторах ,равен .

2. С помощью смешанного произведения можно установить компланарность трех векторов и их ориентацию.

Три вектора компланарны тогда и только тогда, когда .

Если , то система векторов правая.

Если , то система векторов левая.

● Пример 18. Проверить, лежат ли точки ,,,в одной плоскости.

Решение. Если указанные точки лежат в одной плоскости, то векторы ,икомпланарны.,,. Вычислим смешанное произведение этих векторов.. Смешанное произведение равно нулю, поэтому векторы,икомпланарны, а данные точки лежат в одной плоскости.●

● Пример 19. Даны вершины тетраэдра: ,,,. Найти длину высоты тетраэдра, опущенной из вершины(рис.2.22).

Решение. , где- объём тетраэдра,- площадь основания, а- искомая высота. Рис. 2.22 .,,.●

● Пример 20. Показать, что векторы ,,компланарны при любых векторах.

Решение. Первый способ. Учитывая свойства векторного и смешанного произведений, вычислим . Так как смешанное произведение векторовравно нулю, то эти векторы компланарны.

17