5.2. Векторное произведение двух векторов.

Определение векторного произведения.

Определение. Векторным произведением двух векторов иназывается вектор, удовлетворяющий следующим условиям:

а) вектор перпендикулярен плоскости векторов ии направлен так, что тройка векторов,,правая;

б) длина вектора численно равна площади

Рис. 2.19 параллелограмма, построенного на векторах и, т.е., где- угол между векторамии(рис. 2.19).

Очевидно, что ,,,,,.

Пример 11. Проверить справедливость равенства .

Решение. ,,

.

Метод Жуковского.

Рассмотрим метод Жуковского построения вектора .

Пусть угол между векторами иравен.

Векторы иприложим к общему началу(рис. 2.20). Через точкуперпендикулярно векторупроведем плоскость. Из конца вектораопустим перпендикуляр на плоскость. Точку пересечения этого перпендикуляра и плоскости обозначим через. Проведем в плоскостивектори построим вектор.

Рис. 2.20 Покажем, что вектор.

а) Из построения следует, что вектор перпендикулярен векторам,, и векторы,,образуют правую тройку.

б) .

Из а) и б) следует, что .

Если проекцию вектора на плоскостьобозначить через, то

.

Свойства векторного произведения.

Векторное произведение двух векторов обладает следующими свойствами:

1) (векторное произведениеантикоммутативно, т.е. при перестановке сомножителей направление вектора меняется на противоположное, при этом его модуль остаётся неизменным).

Это свойство следует из определения векторного произведения. Если тройка векторов правая, то тройка- левая.

2) (ассоциативный закон). Это свойство легко доказывается из определения векторного произведения.

3) (дистрибутивный закон.) ►.◄

4) . Это свойство следует из определения векторного произведения, а именно из того, что модуль векторного произведения равен площади параллелограмма, построенного на векторахи. Это свойство дает возможность записать в удобной форме параллельность двух векторов.

Например, означает, что векторколлинеарен биссектрисе первого координатного угла.

Векторное произведение в координатной форме.

Пользуясь свойствами векторного произведения и равенствами ,,,,,, вычислим

=

=

, т.е. или.

Применение векторного произведения.

Векторное произведение векторов иприменяется:

для нахождения площади параллелограмма, построенного на векторах и;

для нахождения площади треугольника, построенного на векторах и;

для нахождения синуса угла между векторами и;

для нахождения вектора, перпендикулярного векторам и.

1) Площадь параллелограмма, построенного на векторахи, может быть вычислена по формуле, где- угол между векторамии.

Замечание. Если и, тои. Отсюда следует, чтомодуль определителя второго порядка численно равен площади параллелограмма, построенного на векторах и.

2) Площадь треугольника, построенного на векторахи, равна половине площади параллелограмма, построенного на этих же векторах, т.е., где- угол между векторамии.

3) Синус угла между векторами иможет быть вычислен по формуле.

4) Вектор перпендикулярен векторуи вектору.

Замечание. Векторное произведение может быть использовано при решении системы линейных однородных уравнений вида 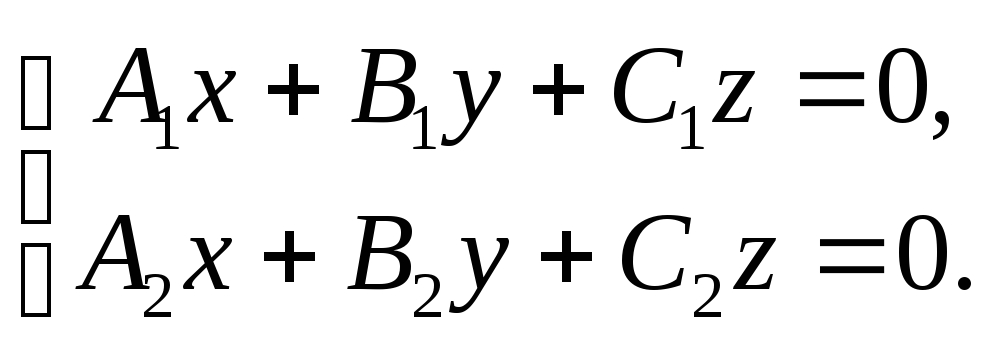Если векторыинеколлинеарны, тоявляется решением исходной системы.

►Действительно, из системы уравнений следует, что вектор перпендикулярен векторами, а, следовательно,.◄

● Пример 12. Дано: ,,,,.

Найти площадь параллелограмма, построенного на векторах и.

Найти синус угла между векторамии.

Решение. Площадь параллелограмма, построенного на векторах иравнамодулю векторного произведения векторов и, т.е...=.

.

Ответ: ,.

● Пример 13. Дано: ,,,,.

Найти значение параметра , при котором векторыиколлинеарны.

Решение. Первый способ. Так как векторы иколлинеарны, то их векторное произведение равно нулю.=0, а так как, тои.

Второй способ. Векторы исоставляют базис системы векторов,,и. В базисеи. Так как векторыиколлинеарны, то, откуда●

● Пример 14. Найти координаты вектора , длина которого равна 15, зная, что он перпендикулярен осии векторуи образует острый угол с осью.

Решение. и, поэтому.

, откуда

Так как вектор образует острый угол с осью, то вторая его координата положительна, тогдаи●

● Пример 15. Найти площадь параллелограмма , если известны координаты трёх его вершин,и.

Решение. .,,,.

● Пример 16. ,,- вершины треугольника. Найти недостающую координатуточки. если площадь треугольникаравна 3.

Решение. Площадь равна половине площади параллелограмма, построенного на векторахи, т.е..

, ,., откуда16,и.

Ответ: или.

● Пример 17. Решить систему

Решение. Из уравнений системы следует, что вектор перпендикулярен векторами. Тогда- решение данной системы. ●