
- •Раздел I. Особенности термодинамики, как науки.
- •I.1. Основные определения термодинамики.
- •Пример 3. Химические реакции и фазовые превращения:
- •Правило знаков для потенциалов:
- •I.2. Теплота, работа, внутренняя энергия.
- •I.3. Равновесные и неравновесные взаимодействия. Статические и нестатические процессы.
- •I.4. Состояния системы. Уравнения состояния системы.
- •I.5. Реальные свойства газа. Уравнение состояния реального газа.
- •I.6. Работа и теплота. Свойства работы и теплоты.
- •I.7. Характеристические функции.
- •Мнемонический приём для термодеформационной системы:
- •I.8. Дифференциальные соотношения термодинамики.
- •Раздел II. Теория теплоёмкостей однородных систем.
- •II.1. Классификация теплоемкостей по единицам количества вещества и видам процессов.
- •II.2. Общая формула теплоёмкостей однородных систем.
- •II.3. Внутренняя энергия и теплоёмкость идеального газа.
- •II.4. Зависимость теплоёмкостей от давления, объёма и температуры.
- •II.5. Зависимость теплоёмкостей от температуры. Истинная и средняя теплоёмкости.
- •Раздел III. Вычисление энтропии.
- •III.1. Три группы формул для вычисления энтропии.
- •III.2. Уравнение адиабаты реального газа в общем виде.
- •Раздел IV. Политропный (политропический) процесс.
- •IV.1. Уравнение политропы. Определение показателя политропы.
- •IV.2. Работа, теплота и внутренняя энергия в политропном процессе.
- •IV.3. Изменение энтропии в политропном процессе.
- •Раздел V. Исследование изопроцессов. Работа, теплота, внутренняя энергия в изопроцессах.
- •Раздел VI. Второй закон термодинамики.
- •V рис. 18. Произвольный прямой обратимый цикл.
Раздел II. Теория теплоёмкостей однородных систем.
II.1. Классификация теплоемкостей по единицам количества вещества и видам процессов.
Однородными называются системы, у которых в различных их частях свойства одинаковые.
Теплоёмкостью называется количество теплоты, необходимое для изменения температуры единицы количества вещества на 1.
В зависимости от того, что является единицей измерения количества вещества, различают:
массовую (удельную) теплоёмкость
 ;
;мольную (молярную) теплоёмкость
 ;
;
Примечание:
1
Кмоль – это количество вещества в
килограммах, численно равное его
молекулярной массе. Например, у сухого
воздуха![]() =28,96
и соответственно его 1 Кмоль имеет массу
28,96 кг.
=28,96
и соответственно его 1 Кмоль имеет массу
28,96 кг.
объёмную теплоёмкость
 .
.
Так как объём вещества зависит от давления и температуры, то объёмные теплоёмкости в справочной литературе, как правило, даются для нормальных физических условий:
рнорм = 101325 Па
Тнорм = 273,15 К
Перечисленные выше теплоемкости, связаны между собой следующими соотношениями
![]() (70)
(70)
![]() (71)
(71)
Из уравнения состояния идеального газа
норм
=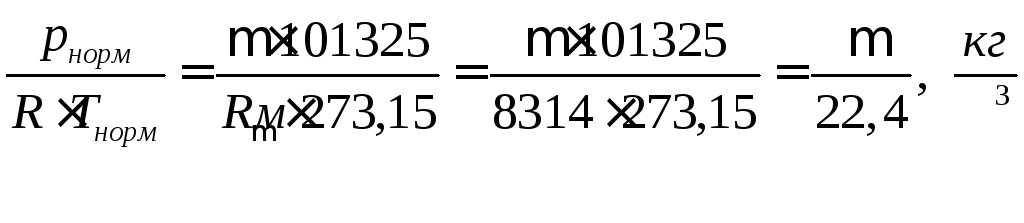
Как
следует из определения теплоёмкости
 ,
ее величина зависит от вида процессов.
Как было показано ранее, теплота
,
ее величина зависит от вида процессов.
Как было показано ранее, теплота![]() является функцией процесса, поэтому и
теплоемкости также подразделяются по
видам термодинамических процессов на
изохорную, изобарную, изотермическую,
адиабатную теплоемкости и теплоемкость
в политропном процессе.
является функцией процесса, поэтому и
теплоемкости также подразделяются по
видам термодинамических процессов на
изохорную, изобарную, изотермическую,
адиабатную теплоемкости и теплоемкость
в политропном процессе.
Теплоемкости
изопроцессов являются теплофизическими
характеристиками вещества и их значения
содержатся в справочниках, но значения
изотермических теплоемкостей и адиабатных
не приводятся, потому что из определения
теплоемкости
 следует:
следует:
cT
= сT
= cWT
= ![]() ;
;
cs = сs = cWs = 0.
Таким образом для изохорного процесса (V=const) используются:
cv – массовая изохорная теплоёмкость (теплоемкость в изохорном процессе).
сv – молярная (мольная) изохорная теплоёмкость;
cWv – объёмная изохорная теплоёмкость.
Для изобарного процесса (p=const) используются:
cp – массовая изобарная теплоёмкость.
сp – молярная (мольная) изобарная теплоёмкость;
cWp – объёмная изобарная теплоёмкость.
Теплоемкость политропного процесса рассматривается далее в разделе IV.
II.2. Общая формула теплоёмкостей однородных систем.
Получим формулу, справедливую для любого газа (идеального, реального) и для любого процесса, включая политропный. Для простоты вывода получим формулу для массовой теплоемкости термодеформационной (тепломеханической) системы.
Из
общего определения массовая теплоемкость
 .
.
Как известно из первого начала термодинамики, для термодеформационной системы
dQ = dU + pdv
Как указывалось выше, внутренняя энергия является функцией состояния, выражаемая, например формулой U=U(T,v). По правилам математики, для полного дифференциала функции нескольких переменных, в этом случае можно записать

Таким образом исходная система уравнений имеет вид:

Решая эту систему методом подстановки, получим следующее выражение
 (72)
(72)
Для изохорного процесса dv=0, тогда из (72)
 (73)
(73)
Формула (73) справедлива как для идеального, так и для реального газов.
В
формуле (72) необходимо знать частную
производную 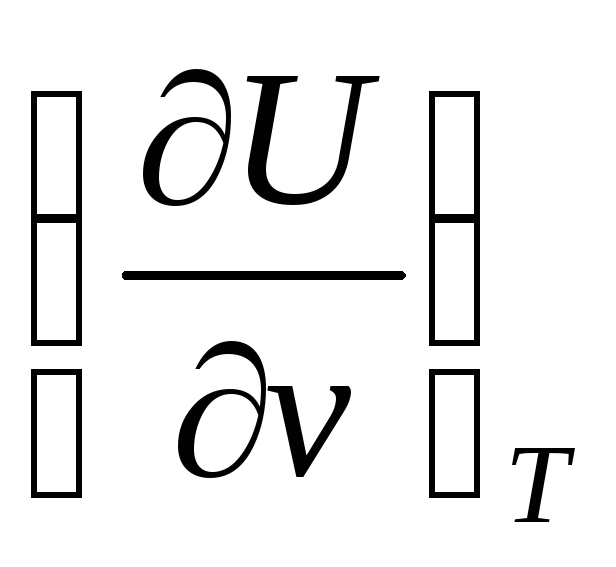 для чего воспользуемся первым началом
термодинамики в виде:
для чего воспользуемся первым началом
термодинамики в виде:
dU = TdS – pdv
Откуда

Частная производная в правой части
 относится
к 3-ему типу дифференциальных соотношений
термодинамики. Тогда
относится
к 3-ему типу дифференциальных соотношений
термодинамики. Тогда

 (73*)
(73*)
Подставим полученное выражение в формулу (72):
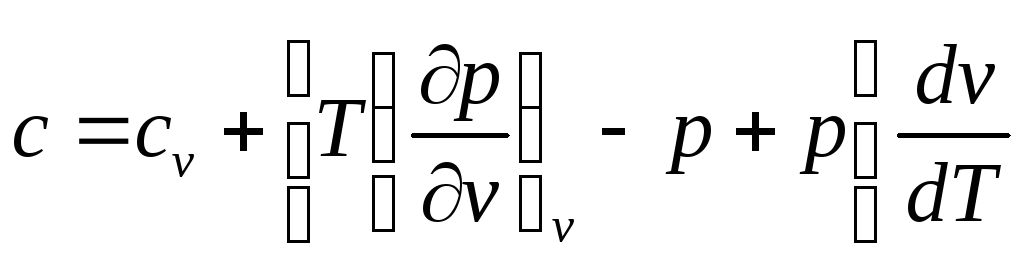

 ,
,
Окончательно получим
![]() (74)
(74)
Формула (74) называется общей формулой для теплоёмкостей однородных систем и справедлива для всех процессов идеального и реального газов.
Например, массовая изобарная теплоёмкость реального газа из (74) запишется в виде
 (75)
(75)
Для политропного процесса уравнение (74) приобретает следующий вид:
 (76)
(76)
