Дискретка_Экзамен_Ответы / графы / 4 эйлеров и гамильтонов циклы

Если граф имеет простой цикл, содержащий все вершины графа (по одному разу), то такой цикл называется гамильтоновым циклом, а граф – гамильтоновым графом. Вопрос о принадлежности графов к классу гамильтоновых решается, как правило, очень трудно. Известны лишь достаточные условия гамильтоновости графов, например, теорема Оре: если для любой пары x и y несмежных вершин графа G порядка n3 выполняется условие d(x)+d(y) n , то G – гамильтонов граф; или теорема Дирака : если для любой вершины x графа G порядка n3 выполняется условие d(x) n/2 , то G – гамильтонов граф. Убедиться в том, что граф гамильтонов можно, например, отыскав в нём один из гамильтоновых циклов, используя метод поиска с возвращением. На рис.4.17 представлена блок-схема рекурсивного алгоритма 4.6 нахождения всех гамильтоновых циклов графа. Этот алгоритм отличается от алгоритма 4.5 нахождения всех простых циклов только условием получения решения, т.к. гамильтонов цикл – это простой цикл, содержащий все вершины графа.

Алгоритм 4.6 получения всех гамильтоновых циклов W в графе G.

Вход: i – заполняемое место в цикле W;

V’ – множество вершин, включенных в цикл.

Выход: последовательность всех гамильтоновых циклов W в графе G, начинающихся вершиной v.

Глобальные параметры: W – формируемый цикл.

Гамильтон(i,V’)

xГ(W_i-1)-V’

W_i := x

i=|V|+1

+

W

Гамильтон(i+1, V’{x})

Конец

Рис.4.17. Рекурсивный алгоритм получения всех

гамильтоновых циклов W в графе G

Если граф имеет цикл (не обязательно простой), содержащий все рёбра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф – эйлеровым графом. Эйлеров цикл содержит не только все рёбра, но и все вершины графа (возможно, по несколько раз). Принадлежность графа классу эйлеровых легко устанавливается теоремой Эйлера: связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин чётны.

Эйлеров цикл представляет собой замкнутую цепь, содержащую все рёбра графа, поэтому можно получить все эйлеровы циклы используя алгоритм 4.2 получения всех цепей заданной длины, изменив в нём условие получения решения. Алгоритм 4.7 получения всех эйлеровых циклов представлен блок-схемой на рис.4.18.

Алгоритм 4.7 получения всех эйлеровых циклов W в графе G.

Вход: i – заполняемое место в цикле W;

E’ – множество рёбер, включенных в цикл.

Выход: последовательность всех эйлеровых циклов W в графе G, начинающихся вершиной v.

Глобальные параметры: W – формируемый цикл;

v – исходная вершина.

Эйлер(i,E’)

xГ(W_i-1)-{y|{W_i-1,y}E’}

W_i := x

x=v и i=|E|+1

+

W

Эйлер(i+1,E’ {W_i-1,x})

Конец

Рис.4.18. Рекурсивный алгоритм получения всех

эйлеровых циклов W в графе G, начинающихся вершиной v

В эйлеровом графе найти один из эйлеровых циклов можно следующим образом:

1. Стек пуст. Множество отмеченных рёбер пусто. Произвольную вершину v положить в стек.

2. Пока стек не пуст, выполнять п.3.

3. x := верхний элемент стека.

Если все рёбра, инцидентные вершине x, отмечены, то взять вершину x из стека и поставить её на очередное место цикла, иначе выбрать неотмеченное ребро {x,y}, отметить его и вершину y положить в стек.

Процесс нахождения эйлерова цикла в эйлеровом графе, диаграмма которого изображена на рис.4.19, представлен в таблице 4.2.

3 1 5

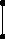
2 4 6

Рис.4.19. Диаграмма эйлерова графа

Таблица 4.2

Процесс нахождения эйлерова цикла

Шаг	Стек	Отмеченные рёбра	Эйлеров цикл
1	1
2	1,4	{1,4}
3	1,4,2	{1,4},{4,2}
4	1,4,2,3	{1,4},{4,2},{2,3}
5	1,4,2,3,1	{1,4},{4,2},{2,3},{3,1}
6	1,4,2,3	{1,4},{4,2},{2,3},{3,1}	1
7	1,4,2	{1,4},{4,2},{2,3},{3,1}	1,3
8	1,4,	{1,4},{4,2},{2,3},{3,1}	1,3,2
9	1,4,5	{1,4},{4,2},{2,3},{3,1},{4,5}	1,3,2
10	1,4,5,6	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6}	1,3,2
11	1,4,5,6,4	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2
12	1,4,5,6	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2,4
13	1,4,5	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2,4,6
14	1,4	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2,4,6,5
15	1	{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2,4,6,5,4
16		{1,4},{4,2},{2,3},{3,1},{4,5},{5,6},{6,4}	1,3,2,4,6,5,4,1