Федеральное агентство по образованию

Белгородский государственный технологический университет

им. В.Г.Шухова

Кафедра стратегического управления ргз №1

по дисциплине “Экономико-математическое моделирование”

Вариант №9

Выполнили:

студенты гр. МК-31

Смирных Т. А.

Литвинова А. А.

Проверили:

Борачук В.В.

Гавриловская С. П.

Белгород 2011 г.

Введение

Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств, относятся к задачам линейного программирования

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:

• математические модели очень большого числа экономических задач линейны относительно искомых переменных;

• эти типы задач в настоящее время наиболее изучены;

• для решения этих задач разработаны специальные конечные методы и соответствующие стандартные программы для их решения на ЭВМ;

• многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;

• некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции Z), которые удовлетворяют системе ограничений, называетсядопустимым планомзадачи линейного программирования. Функция Z , максимум или минимум которой определяется, называетсяцелевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции Z, называетсяоптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

Задача линейного программирования в стандартной форме с двумя переменными имеет вид:

Z = C₀ + C₁X₁ + C₂X₂ + . . . + C_nX_n  max,

х₁0, х₂0

Контрольное задание № 1

Требуется:

а) сформулировать экономико-математическую модель задачи в виде ЗЛП;

б) привести ЗЛП к канонической форме;

в) построить многогранник решений (область допустимых решений) и найти оптимальную производственную программу путем перебора его вершин и геометрическим способом;

г) решить задачу с помощью симплекс-таблиц.

Постановка задачи:

Для производства двух видов продукции А и Б используются три типа ресурсов. Нормы затрат ресурсов на производство единицы продукции каждого вида, цена единицы продукции каждого вида, а также запасы ресурсов, которые могут быть использованы предприятием, приведены в табл. 1.1.

Таблица 1.1.

Типы ресурсов	Нормы затрат ресурс на единицу продукции		Запасы ресурсов
	А	Б
Электроэнергия	1	2	56
Сырье	2	1	80
Оборудование	3	1	117
Цена ед. продукции	3	2

Требуется определить такие объемы выпуска продукции А и В, чтобы при использовании трех типов ресурсов выручка от ее реализации была максимальной.

Обозначим через Х₁и Х₂количество продукции А и В, которую планируется произвести с использованием трех типов ресурсов. Стоимость произведенной продукции Z = C₁X₁+ C₂X₂. Мы должны определить X₁и X₂так, чтобы величина Z была максимальной. Переменные X₁, X₂не могут принимать произвольных значений. Их значения ограничены условиями производства, а именно тем, что существует определенный запас каждого вида ресурса на изготовление продукции. На изготовление продукции А затраты по видам ресурсов: электроэнергия, сырье, оборудование; соответственно равны: X₁, 2X₁, 3 X₁. На продукцию В соответственно: 2* X₂, X_2, X₂. При этом должны выполнятся такие условия, где сумма затрат каждого вида ресурса, затраченного на производство продукции двух видов, не превышает количество реального запаса или равна запасам, т. е. при использовании электроэнергии неравенство выглядит следующим образом: X₁ + 2* X₂ 56, соответственно для сырья и оборудования:2 X₁ + X₂ 80, 3* X₁ + X₂ 117. Кроме того, величины Х_1,Х₂ не могут быть отрицательными: Х₁ 0, Х₂ 0.

Таким образом, задача заключается в нахождении точки максимума функции Z среди точек с координатами X₁,X₂, которые удовлетворяют неравенствам.

Решим геометрически задачу при С₁= 3, С₂= 2

Z= 30*Х₁ + 20*Х₂ max

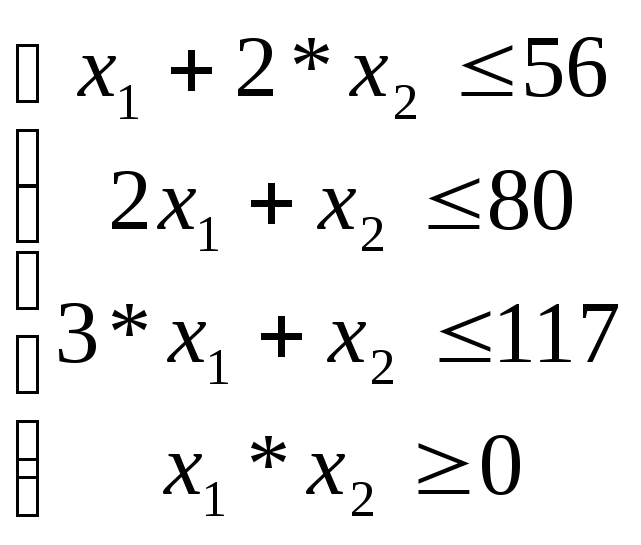
Построим на плоскости множество решений системы неравенств:

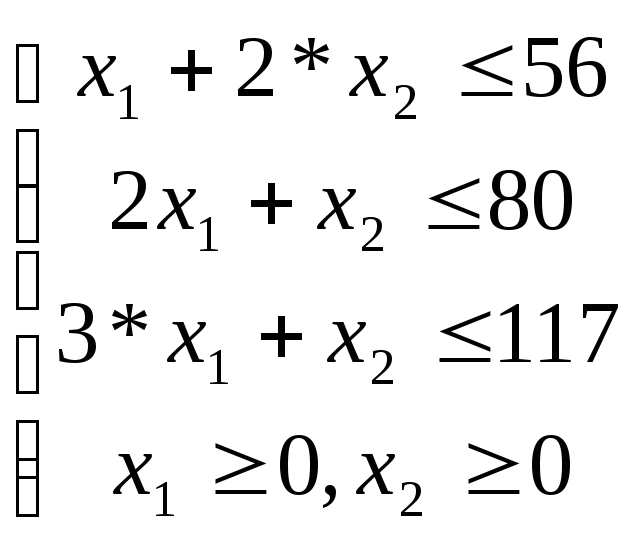
Решим геометрически задачу при С₁= 3, с₂= 2

Решим уравнение х₁+2*х₂=56 и найдем точки пересечения с осями координат:

(0;28), (56;0).

Решим уравнение 2х₁+ х₂=80 и найдем точки пересечения с осями координат:

(0;80), (40;0).

Решим уравнение 3*х₁+х₂=117 и найдем точки пересечения с осями координат:

(0;117), (39;0).

Точкой максимума здесь является точка B, являющейся точкой пересечения прямой 3*х₁+*х₂=117 и прямой х₁+2*х₂=56 и имеет координаты (х₁;х₂). Для того чтобы найти координаты этой точки необходимо решить уравнение:

8*х₁+4*х₂=14, приx₁ = 0

В результате получим точку B(0;3,5).

Теперь необходимо найти стоимость продукции в отдельных точках:

Точка О (0;0): Z= 30*3+2*0=0

Точка A(28;0):Z=3*28+2*0=84

Точка B(35,6;10,2):Z=3*35,6+2*10,2=127,2

Точка C(40;0):Z=3*40+2*0=120

В результате метода перебора вершин максимальная прибыль находится в точке Bи равна 127,2у.е.

Множеством точек на плоскости, удовлетворяющих системе ограничений, называют часто допустимым многоугольником. Эта область может быть неограниченной или вовсе пустой.

Целевая функция задачи примера 2 геометрически изображается с помощью прямой уровня, т.е. прямой, на которой Z = C₀+ C₁X₁+ C₂X₂принимает постоянное значение. Если С - произвольная константа, то уравнение прямой уровня имеет вид

C₀+C₁X₁+C₂X₂=C.

При изменении константы C получаем различные прямые, параллельные друг другу. При увеличении C прямая уровня перемещается в направлении наискорейшего возрастания функции Z, т.е. в направлении ее градиента. Вектор градиента

.

Геометрический метод решения задачи состоит в следующем. Строится допустимый многоугольник и принимается некоторое положение линии уровня целевой функции. Определяется направление перемещения прямой уровня. Точкой минимума Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой максимума - точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника.

Точка с координатами (35,6;10,2) является точкой максимума Z_max=127,2