42.Теорема о непрерывных функциях

Определение 1. Функция f(x) называется непрерывной в точке x0, если .Дадим несколько расшифровок этого важнейшего определения.

.Определение 2. Функция f(x) называется непрерывной в точке х₀ слева (справа) если f(x₀)=f(x₀ – 0) (f(x₀)=f(x₀+0)). Очевидно,что непрерывность в точке х₀ означает непрерывность слева и справа одновременно.

Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, т.е. если

Обратите внимание, где стоит квантор, это важно.

Определение. Если функция f(x) не является непрерывной в точке х₀, то говорят, что в точке х₀ функция f(x) имеет разрыв.

Теорема о непрерывности сложной функции.Пусть функция (t) непрерывна в точке t₀ и функция f(x) непрерывна в точке х₀=(t₀). Тогда функция f((t)) непрерывна в точке t₀.

Доказательство.Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем

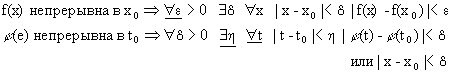
Выписывая подчеркнутые кванторы, получим, что

,что и говорит о том, что f((t)) непрерывна в точке t₀. 

Обратите внимание на следующие детали:а) т.к. x=(t), то |(t)-(t₀)|< может быть записано как |x-x₀|<, и f(x) превращается в F((t));

б) при определении непрерывности (t) в точке t₀ в первом кванторе стоит буква . Это необходимо для согласования с квантором  в предыдущей строке и взаимного уничтожения . Любая другая буква на этом месте не дала бы верного результата.

Теоремы о непрерывных функцияхПерейдем к доказательству важнейших теорем о непрерывных функциях.Первая теорема Больцано-Коши.Пусть f(x) определена и непрерывна на отрезке [a,b] и на концах этого отрезка принимает разные по знаку значения.Тогда существует такая точка с принадлежащая [а,b] в которой f(c)=0.Доказательство.Пусть, для определенности, f(a)<0, f(b)>0. Ситуация выглядит так:

Для доказательства теоремы снова используем метод деления отрезка пополам.

1Деление отрезков пополам.

Разделим отрезок [a, b] пополам. Середина его будет точка . Тогда возможны такие варианты:а). В этом случае, взяв , теорему можно считать доказанной.

б) . В этом случае для дальнейшего рассмотрения оставим отрезок , который обозначим [a₁, b₁].

в) В этом случае для дальнейшего рассмотрения оставим отрезок , который обозначим [a₁, b₁].

Проделаем такую же процедуру с отрезком [a₁, b₁], получив отрезок [a₂, b₂], затем то же самое с отрезком [a₂, b₂], получив отрезок [a₃, b₃] и т.д. Заметим, что для дальнейшего рассмотрения все время оставляется тот отрезок, для которого f(a_n)<0 и f(b_n)>0.

Вторая теорема Больцано-Коши. Пустьf(x) определена и непрерывна на отрезке <a,b> и . Тогда m<C<M с<a,b> f(c)=C.

Первая теорема Вейерштрасса.

Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a, b]. Тогда она ограничена на этом отрезке, т.е. существуют такие числа m и M, что x принадлежащего [a,b] f(x) больше либо равно m и меньше либо равно M.

Доказательство.Доказательство этой теоремы проведем методом от противного.

Предположим противное – пусть, например, функция f(x) неограничена сверху.

1.Построение последовательности. Мы предположили, что f(x) неограничена сверху на [a,b]. Это означает, что для любого числа А найдется такая точка x[a,b], что f(x)>A.Возьмем в качестве числа А числа 1, 2, 3, 4,… Тогда , что f(x_n)>n.Мы получили, таким образом, некоторую последовательность {x_n}[a,b] и удовлетворяющую свойству f(x_n)>n.

2.Выделение подпоследовательности. Так как последовательность {x_n} ограничена, то по лемме Больцано-Вейерштрасса з нее можно выделить сходящуюся последовательность {x_n}, т.е. . В силу замкнутостиотрезка [a, b] точка c [a,b]. (Отметим,что в этом месте используется ограничение теоремы – замкнутость [a,b]. Если бы, например, был (a,b), то с могла бы и не принадлежать (a,b)).

1.Сведение к противоречию.Т.к. согласно п.1 , то, переходя к пределу kполучим т.е. f(c)=+, что противоречит условию теоремы, где сказано, что f(x) определена на отрезке [a,b],что означает, что f(c) должна иметь конечное значение. 

Вторая теорема Вейерштрасса.Пусть функция f(x) определена и непрерывна на замкнутом отрезке[a,b]. Тогда существуют такие точки x₁, x₂ принадлежащие [a,b], что , т.е. инфимум и супремум f(x) достигаются на [a,b].

пример

Используя определение непрерывности в терминах приращений, доказать, что функция непрерывна в произвольной точке x = a.

Решение.

Условие непрерывности по Гейне можно записать в виде

      

где Δx и Δy − малые приращения, показанные на рисунке 3. Для заданной функции справедливы следующие соотношения в точке x = a:

      

Следовательно,

      

Вычислим предел.

      

43.точка разрыва функции и их классификация

Определение: Точка ,в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1.функция  определена в точке и ее окрестности;

2.существует конечный предел функции  в точке ;

3. это предел равен значению функции в точке , т.е. 

называется точкой разрыва функции. Точка разрыва первого рода

Определение

Если в точке  существуют конечные пределы  и , такие, что , то точка  называется точкой разрыва первого рода.

Пример

Функция  в точке  имеет разрыв первого рода, так как

, а 

Точка разрыва второго рода

Определение

Если хотя б один из пределов  или  не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Пример

Для функции  точка  - точка разрыва второго рода, так как  .Точка устранимого разрыва

Определение

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке :  или функция  не определена в точке , то точка  называется точкой устранимого разрыва.

Пример

Рассмотрим функцию  . Найдем односторонние пределы и значение функции в точке :

Так как  и не равны значению функции в точке, то точка  - точка устранимого разрыва.

45.Производная функции, ее геометрический и механический смысл.

Производной функции y = f(x) в точке Х называется предел, если он существует, отношения приращения функции к приращению аргумента при стремлении последнего к нулю.

Производная функции в точке интерпретируется:

1.      механически – как мгновенная скорость изменения функции в этой точке

2.      геометрически – как угловой коэффициент касательной к графику функции в этой точке.

Механический смысл:

Зная закон S = f(t) движения точки, найти V ее движения в любой момент времени. Зафиксируем момент времени t и t + t;

За время t точка пройдет S(t), за t + t = s(t + t) – f(x)

За время t  S = f(t + t) – f(t)

Отношение   - характеризует среднюю скорость Vср. за t

Если в этом отношении перейти к пределу при t  0, то получим истинную (мгновенную) скорость движения точки в момент t:

Геометрический смысл:

геометрически производная представляет собой угловой коэффициент касательной к графику этой функции.

Уравнение искомой касательной запишем в виде уравнения прямой, проходящей через т.М(Х₀, У₀), т.е.

У-У₀ = к(Х-Х₀), где неизвестен только коэф. – к, равный тангенсу угла наклона касательной к положительному направлению оси ОХ. Т.о. задача свелась к нахождению к = tg

Пусть кривая L задана функцией y = f(x), МТ – касательная к кривой в т.М(Х₀, У₀). На кривой L возьмем производную т.W(Х₀+Х, У₀+У) и проведем секущую MW. Из тр-ка МКW определим угловой коэф-т секущей MW: 

Если W  М, то     и  tg  tg,  , а т.к. при W  М х  0, то  

Согласно определению, для отыскания производной функции y = f(x) в т.Х необходимо проделать 4 операции:

1.      придать Х приращение Х, т.е. перейти к точке Х+Х

2.      вычислить приращение функции У = f(Х+Х)-f(X)

3.      составить соотношение У/Х

4.      вычислить 

46. понятие о дифференцированности функции

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке)