2.3.Теплопроводность газов

Если в некоторой среде создать вдоль оси z градиент темпера­туры, то возникает поток тепла, величина которого определяется формулой

(2.8)

где q — поток тепла через поверхность S, расположенную перпен­дикулярно к оси z, dT/dz — градиент температуры (точнее, проек­ция градиента температуры на ось z), к — коэффициент пропорцио­нальности, зависящий от свойств среды и называемый коэффи­циентом теплопроводности. Единицей q служит Дж/с, т. е. Вт (ватт). Следовательно, к измеряется в ваттах на квадратный метр-кельвин, Вт/(м²·К). Знак минус в формуле отражает то обстоятельство, что тепло течет в направлении убывания температуры. Поэтому знаки q и dT/dz противоположны.

Уравнение (2.8) есть эмпирическое уравнение теплопровод­ности. Его называют также законом Фурье.

В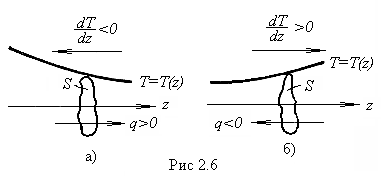ычислим поток тепла в газе, основываясь на моле­кулярно-кинетических представлениях. Если температура газа в разных точках различна, то и средняя энергия молекул в этих точках также будет различна. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят запасенную ими энергию. Этот перенос энергии и обусловливает процесс тепло­проводности в газах (рис.2.6).

Рассмотрим газ, в котором каким-то способом поддерживается непостоянство температуры вдоль направления z. Представим мысленно площадку S, перпендикуляр­ную к этому направлению (рис.2. 7).

Будем считать, что коли­чество молекул, пролетающих через площадку S за секунду, равно

Каждая молекула несет с собой энергию, соответствующую тем­пературе в том месте, где произошло последнее соударение ее с дру­гой молекулой. Молекулам, летящим вдоль осиz, следует приписывать энер­гию ε₁, отвечающую темпера­туре Т₁ в плоскости (z - λ), мо­лекулам же, летящим в противо­положном направлении, — энер­гию ε₂, отвечающую темпера­туре T₂ в плоскости (z + λ) (z — координата плоскости S, см. рис.2. 7).

Числа частиц, летящих через площадку S во встречных направлениях, не могут быть различными. Если бы они оказались неодинаковыми, то, кроме потока тепла через площадку S, наблюдался бы поток вещества — происходило бы перемещение газа из одной части пространства в другую. Мы же предполагаем, что движение газа, как целого, отсутствует. Тогда количество энергии, переносимое молекулами за се­кунду через площадку S в положительном направлении оси z, равно

Разность T₁ – T₂ = T (z – λ) – T (z + λ). Ввиду малости λ эту разность можно представить в виде , гдеdT/dz — производная Т по z в том месте, где расположена плоскость S. Тогда количество энергии

Умножим и разделим это выражение на массу молекулы m и на число Авогадро N_A:

Учтя, что nm = ρ, и (c_v — удельная теплоемкость при постоянном объеме, - молярная масса вещества), можно напи­сать:

Эта формула определяет поток тепла через поверхность S. Коэффициент пропорциональности, как следует из (2.8), есть коэффициент теплопро­водности газов

Выясним зависимость κ от величин, характеризующих моле­кулу, и от параметров газа. Поскольку κ ~, подставим

В результате получается, что Эта зависимость отличается от зависимости дляη тем, что κ обратно пропорционален , в то время какη прямо пропорционален . Кроме того, κ зависит от числа и характера степеней свободы моле­кулы (от числаi). Зависимость от давления и температуры у κ такая же, как и у η. Следовательно, коэффициент теплопроводности не зависит от давления (до тех пор, пока λ не становится того же по­рядка, что и линейный размер сосуда, вдоль которого передается тепло) и возрастает с температурой несколько быстрее, чем .