Физика лекции / мкт физика / Лекция 11

Лекция 11

6.Флуктуации

6.1.Общие сведения о флуктуациях

Согласно второму началу термодинамики, самопроизвольные процессы ведут систему к наиболее вероятному состоянию - к возрастанию энтропии. После того, как энтропия системы стала максимальной, дальнейшие изменения в системе прекращаются - достигнуто равновесие.

Однако состояние равновесия совсем не означает внутреннего покоя; внутри системы проходят непрерывные тепловые движения. Таким образом, любое физическое тело в каждое мгновение перестает быть самим собой, взаимное расположение молекул в каждое мгновение не такое, как в предыдущее, и значения всех физических величин сохраняются лишь в среднем, они не строго равны своим вероятным значениям, а колеблются около эти значений.

Отклонение от равновесных, наиболее вероятных значений называется флуктуацией. Величины разных флуктуаций крайне незначительны. Чем больше величина флуктуации, тем она менее вероятна.

Рассмотрим физическую величину, истинное значение которой равно Х, ее среднее значение <X>, тогда отклонение Х=Х - <X> не может быть мерой флуктуации, оно меняется во времени, величина же <X>=0 , т.к. имеют место равновероятные отклонения в обе стороны.

Мерой флуктуации физической величины Х является средняя величина квадрата разности Х

<(X)²>=<(X - <X>)²>=<X²> - (<X>)^{2 ,}

которая называется квадратичной флуктуацией, <(X)²> 0.

Абсолютной флуктуацией называется величина .

Относительная флуктуация - это отношение абсолютной флуктуации к среднему значению .

Флуктуации заметны для систем с небольшим числом частиц и совсем незаметны для больших тел с огромным числом молекул.

Исследования показали, что изменение плотности, давления и температуры газа, находящегося в 1 см³ , составляет 10^-8 % . Такие флуктуации слишком малы, чтобы их можно было обнаружить опытом.

Иначе обстоит дело в объеме кубического микрона. Здесь число частиц N=, и флуктуации достигают измеримых величин (сотые доли %).

Флуктуация представляет собой “ненормальное” явление в том смысле, что она приводит к переходу от более вероятного состояния к менее вероятному. Во время флуктуации тепло переходит от холодного тела к горячему, нарушается равномерное распределение молекул, возникает упорядоченное движение.

Хотя флуктуации возникают непрерывно, они не оказывают влияния на общий ход физических процессов, энтропия процессов возрастает.

Пусть Х - некоторая физическая величина, характеризующая замкнутую макросистему в целом (например, объем, температура). Будем считать, что из Х уже вычли среднее значение этой величины (например, Х=Т - <T>), поэтому <X>=0. Распределение вероятностей для энергии замкнутой системы дает формула Больцмана .

Вероятность того, что величина принимает значения в интервале X ; X+dX, равна

Р(Х)dХ=const exp(S(Х)),

где S - энтропия системы в состоянии Х.

В состоянии энтропия системы S максимальна, поэтому

.

Величина Х при флуктуации мала и функцию S(Х) можно разложить в ряд:

,

или где =const>0 , тогда

Р(Х)dХ=Aexp(- Х²/2)dХ – это распределение Гаусса (рис.6.1).

6.2. Флуктуации термодинамических величин

Рассмотрим флуктуации, которые происходят в квазизамкнутой макроскопической системе А, погруженный в термостат В с температурой (Т=<>). Будем считать, что флуктуация происходит только в системе А, при этом термостат участвует в квазистатическом процессе. Состояние системы определяется параметром Х, который в состоянии равновесия равен нулю, а в конечном флуктуационном состоянии Х0. Пусть изменение Х происходит достаточно медленно, поэтому равновесие в системе А при флуктуации не нарушается. При изменении параметра Х изменяются так же значения термодинамических величин, которые могут быть определены из первого и второго начал термодинамики.

Процесс перехода макроскопической системы из начального состояния в конечное ( флуктуацию) можно рассматривать как действие некоторого воображаемого источника работы. Работу этого источника при изменении Х от 0 до Х обозначим А(Х). Полное изменение энтропии замкнутой системы, состоящей из термодинамической системы А и термостата В, равно:

S=S_A + S_B,

S_A - изменение энтропии системы А, S_B - изменение энтропии термостата В.

Для определения изменения энтропии S_A системы А, в которой возможна флуктуация параметра Х, обозначим работу внешнего источника А, тогда изменение энтропии системы согласно основному термодинамическому неравенству будет равно

.

Здесь и - равновесные значения температуры и давления системы А, - внутренняя энергия, объем системы А, - работа, совершаемая системой (или над системой).

Аналогично, изменение энтропии термостата равно: .

Система А и термостат В образуют замкнутую систему, поэтому выполняются законы сохранения объема (при постоянном давлении, p=const) и энергии . Тогда полное изменение энтропии

.

Подставив это выражение в функцию распределения величины Х, имеем:

- мерой вероятности малых флуктуаций в макроскопической системе А является работа, которую надо над ней совершить для изменения параметра х от нуля до некоторого значения. Величина работы А количественно определяет меру флуктуации.

Определим величину этой работы. Ввиду малости флуктуации переход системы из начального в конечное состояние будем считать равновесным, тогда

A=U_A - S_A + p_OV_A.

Рассмотрим изотермический процесс, =const. В этом случае

A=(U_A - S)+p_OV_A,

величина U_A - S_A=F_A - свободная энергия (или термодинамический потенциал Гельмгольца) макроскопической системы А, тогда d(U - TS)=dF= -pdV , или Отсюда

(6.1)

но A=F+p_OV, следовательно,

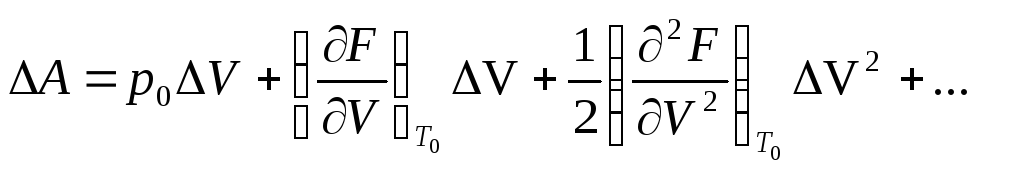(6.2)

(F разложили в ряд). Подставляя (6.1) в (6.2) имеем:

(6.3)

Флуктуация рассматривается как равновесный процесс, поэтому , и

(6.4)

Тогда вероятность того, что обьем системы находится между V и V+dV равна:

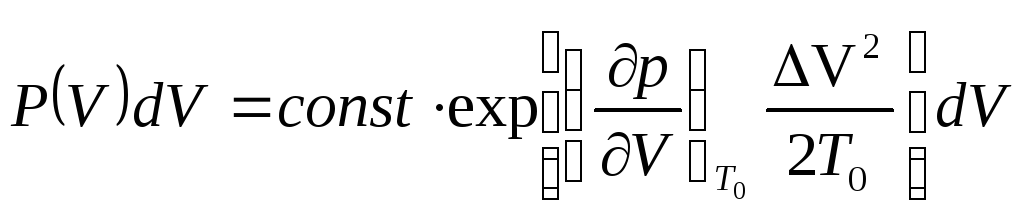. (6.5)

Из (6.5) следует, что производная должна быть отрицательной . Если бы это условие не выполнялось, вероятность флуктуации не убывала бы с ростом ее масштаба и система находилась бы в неустойчивом состоянии.

Таким образом, первое условие устойчивости состояний имеет вид

(6.6)

Если это условие выполняется, то постоянная, входящая в (6.5) равна:

.

Найдем теперь распределение вероятности, определяющее флуктуацию температуры при постоянном объеме. Для этого определим работу, которую нужно совершить над системой А для того, чтобы перевести ее из начального состояния с постоянной температурой в конечное с температурой +dT. Для изменения энтропии имеем:

,

т.к. , тогда .

Разложим изменение внутренней энергии U в ряд по малым степеням S, учитывая, что , получаем

но , тогда

(здесь учли определение теплоемкости C_V=Q_V/T и Q_V=TS).

Вероятность того, что температура макроскопической системы А испытывает флуктуацию и меняется в интервале T, T+dT равна

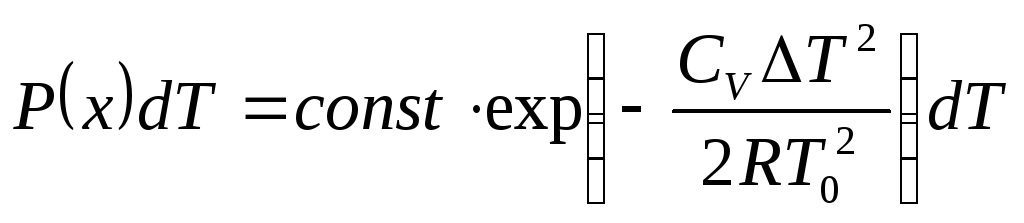. (6.7)

Из выражения (6.7) следует второе условие устойчивости состояний:

C_V>0 - теплоемкость однородного вещества при постоянном объеме должна быть существенно положительной величиной.

Лекция 9

Газ Ван-дер-Ваальса

До сих пор мы не выходили за рамки модели идеального газа, подчиняющегося уравнению Менделеева – Клапейрона . Однако с ростом давления при постоянной температуре оказывается, что . При р= 1000 атм. величина ста­новится вдвое больше, чем предписывает модель идеального газа (газ не «сжимается»). Причин этому две:

1) собственный размер молекул; он и уменьшает объем, до­ступный для движения молекул, при нормальных условиях он составляет ~0,07 % объема сосуда с газом, а при 100 атм. уже ~70% ;

2) сложный характер взаимодействия между молекулами.

Типичная кривая зависимости энергии взаимодействия Uвз от расстояния г между их центрами приведена на рис. 1. На малых рас­стояниях () молеку­лы отталкиваются, на бо­льших () притягива­ются.

Э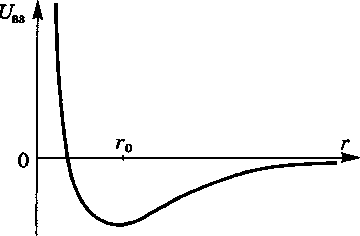ти причины можно учесть путем введения по­правок в уравнение состо­яния идеальных газов, что и сделал Ван-дер-Ваальс.

Рис. 1.

В результате уравнение состояния одного моля реального газа приняло вид

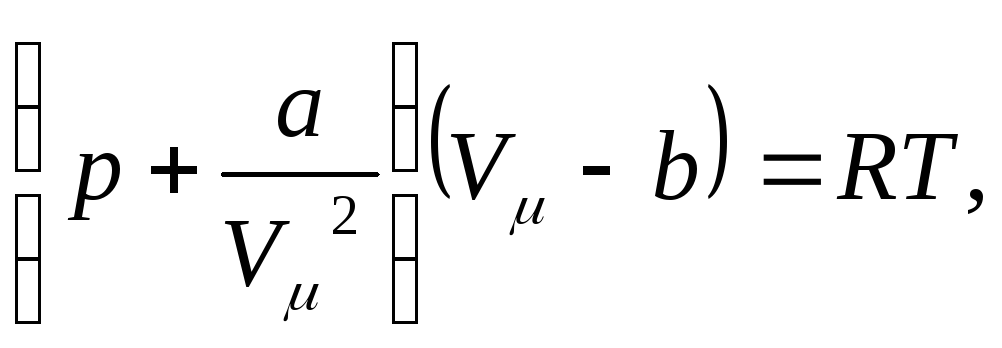(1)

Это и есть уравнение Ван-дер-Ваальса. Здесь а и b — посто­янные Ван-дер-Ваальса, для разных газов они имеют свои зна­чения.

Если мы имеем дело не с одним, а с молями газа объемом V, то в уравнении (1) следует сделать замену:

.

2

Поправка в первой скобке, , обусловлена силами при­тяжения между молекулами. Она имеет размерность давления, и ее часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление р. Однако, если бы силы притя­жения между молекулами мгновенно исчезли, то давление на стенку стало бы . Т.е. при переходе от идеального газа к реальному давление на стенку уменьшается из-за сил при­тяжения между молекулами.

Поправка b связана с собственным объемом молекул, ее размерность м /моль.

Газ, подчиняющийся уравнению (1), называют ван-дер-ваальсовским. Уравнение Ван-дер-Ваальса при большой простоте дает возможность качественно объяснить широкий круг явлений в га­зах и в жидкостях.

Найдем давление, при котором плотность углекислого газа с температурой Т= 300 К равна = 500 г/л. Считая газ ван-дер-ваальсовским, представим (1) в виде

Подставив и , получим: .

Д

6

2

-6

3

ля углекислого газа а = 0,367 Па·м /моль , b = 4,3·10 м /моль и = 44 г/моль. В результате подстановки найдем р 80 атм. Расчет же по формуле состояния идеального газа дает 280 атм. Различие весьма значительное.

Найдем энергию ван-дер-ваальсовского газа. Внутренняя энергия такого газа , где — суммарная кинетическая энергия молекул в Ц-системе(связанной с сосудом), — суммар­ная энергия взаимодействий молекул(собственная потенциаль­ная энергия). Найдем . Работа сил притяжения равна убыли внутренней энергии . Силы притяжения характеризуются внутренним дав­лением в уравнении Ван-дер-Ваальса. Тогда элементарная рабо­та этих сил , где знак минус обусловлен тем, что при расширении газа (>0) работа d'А должна быть отрица­тельной, d’A < 0. Итак,

.

Мы представили d'А как убыль некоторой величины — она и является энергией =. При .

Суммарная же кинетическая энергия зависит от поступа­тельного и внутреннего движений молекул, и определяется как . Таким образом, внутренняя энергия моля ван-дер-ваальсовского газа

где .

Если газ расширяется в пустоту без теплообмена с окружаю­щими телами, то А = U, Q = 0, и согласно первому началу в этом процессе V = сопst. Значит, с ростом объе­ма температура газа уменьшается (в отличие от идеального газа).

U=const

Ек˜= сVT

Uвз

Это можно представить и нагляд­но (рис. 2). Видно, что при расши­рении газа (увеличении объема V) в случае U=const суммарная кинети­ческая энергия молекул газа, а зна­чит и температура T, уменьшается. Газ охлаждается.

Получим для моля ван-дер-ваальсовского газа этого газа уравнение адиабаты в переменных T, V, если известна его молярная теп­лоемкость . Согласно первому началу термодинамики

.

Отсюда

Интегрируя это уравнение, получаем , или

.

Таким образом, уравнение адиабаты имеет вид .

Определим для ван-дер-ваальсовского газа разность молярных теплоемкостей . По определению теплоемкости

Учитывая, что получим

. (1)

Найдем (dV/dT)p. Для этого продифференцируем по T уравнение Ван-дер-Ваальса. В результате получим

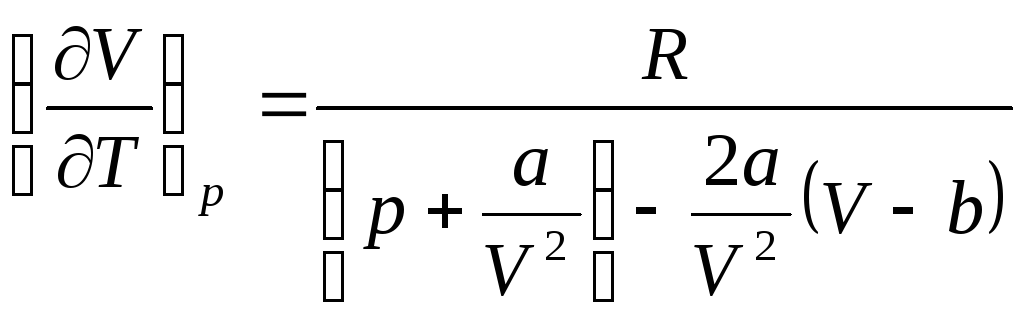. (2)

Подстановка (2) в (1) приводит к искомому результату:

.

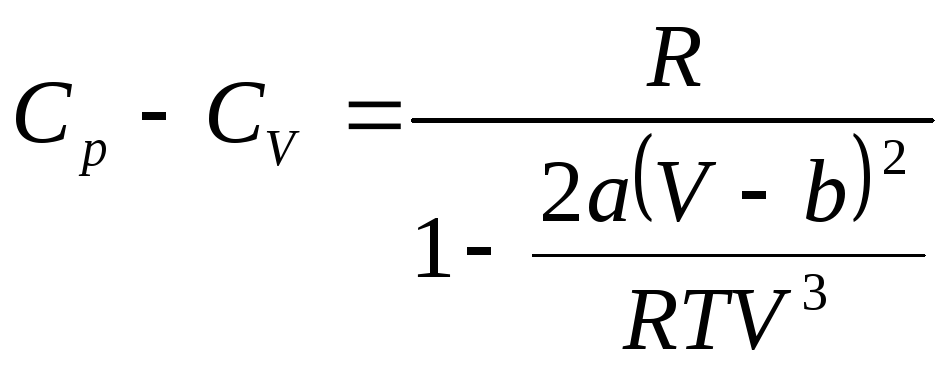ЭФФЕКТ ДЖОУЛЯ-ТОМСОНА

Пропуская газ по теплоизолированной трубке с пористой перегородкой, Джоуль и Томсон обнаружили, что при расширении, которым сопровождается прохождение газа через перегородку, температура его несколько изменяется. В зависимости от начальных давления и температуры имеет тот или иной знак и может быть =0. Это явление было названо явлением Джоуля-Томсона. Если <0 , температура понижается, эффект считается положительным; если >0, газ нагревается, эффект считается отрицательным.

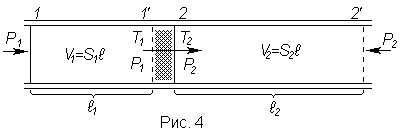Схема опыта представлена на рис. 3. По трубе с крайне плохо проводящими тепло стенками устанавливается стационарное течение газа. В трубке имеется перегородка с мелкими порами (пробка из ваты), на которой происходит перепад давления от большого значения до малого значения , в результате чего газ сильно расширяется. Разность температур фиксируется.

Выделим мысленно часть газа, ограниченную сечениями 1 и 2. По мере движения газа по трубе эти сечения перемещаются и спустя некоторое время оказываются в положениях и соответственно. Так как за перегородкой та же порция газа занимает больший объем, чем перед перегородкой, сечение 2 переместится на больший отрезок, чем сечение 1. Расширение газа происходит без теплообмена с внешней средой ( процесс адиабатный), приращение внутренней энергии газа равно совершенной над ним работе:

(3)

Работу над данной порцией газа совершает граничащий с ней газ. Слева на выделенную часть газа действует сила ( S - сечение трубки), направленная в сторону движения. Справа действует сила , противодействующая движению. В итоге над рассматриваемой массой газа совершается работа:

Здесь - объем, занимаемый газом до расширения, - объем газа после расширения. Тогда

(4)

С учетом (4) выражение (3) принимает вид

(5)

Таким образом, в опыте Джоуля- Томсона сохраняется величина , называемая теплосодержанием или энтальпией.

Проведем расчет для моля газа. После расширения газ имеет большой объем, и его можно считать идеальным, до расширения – газ вандерваальсов, поэтому

Для внутренней энергии Подставив в (5), получаем

Преобразуем Тогда

и Знак определяется знаком выражения, стоящего в скобках. Нулевой эффект =0 достигается при условии

Этому уравнению соответствует на плоскости () кривая (рис.4). Точки этой кривой определяют значения параметров , при которых . Точки, лежащие выше кривой, определяют значения , при которых , т.е. эффект отрицателен, при перемещении вверх от кривой первое слагаемое в скобках растет, скобка становится больше нуля). Точки, лежащие ниже кривой, определяют , при которых эффект положителен. Кривая на рис.4 называется кривой инверсии. Таким образом, знак и величина эффекта определяются начальной температурой и начальным объемом. При эффект всегда отрицательный. При эффект будет положительным только при достаточно большом начальном объеме (т.е. при достаточно малом начальном давлении).

При данном начальном объеме (давлении) величина линейно изменяется с начальной температурой (рис.5). Чем ниже начальная температура, тем сильнее охлаждается газ в результате эффекта Джоуля-Томсона.

Эффект Джоуля-Томсона обусловлен только отклонением газа от идеальности. Для идеального газа и выражение (5) принимает вид

т.е.