6.4. Колебания одномерной решетки с базисом

Мы рассмотрели колебания одномерной моноатомной решетки Бравэ. Рассмотрим теперь продольные колебания атомов одномерной решетки с базисом, когда на линейную элементарную решетку Бравэ с параметром 2а приходится два атома. Пусть вдоль прямой линии располагаетсяN ячеек. Такая система обладает 2Nстепенями свободы. При решении задачи о колебаниях атомов в такой системе воспользуемся следующей моделью. Рассмотрим двухатомную линейную цепочку (рис.6.7), вдоль которой поочередно располагаются атомы с различными массамиM₁иM₂, а силы между парами соседних атомов одинаковы (атомы связаны между собой пружинками одинаковой жесткости). Пружинка моделирует силы притяжения, когда она растянута, и силы отталкивания, когда она сжата.

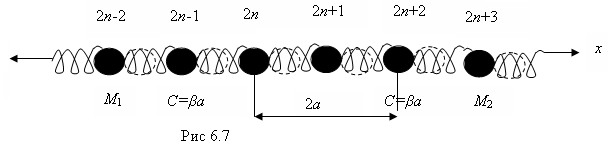
Обозначим 2naчетные положения равновесия атомов с массойМ₁, а (2n+1)a-нечетные для атомов с массойМ₂. Пустьи_2nесть смещение атома с массойМ₁вдоль направленияхв момент времениtотносительно его положения равновесия, аи_2n+1 - смещение атома с массойМ₂из его положения равновесия.

Будем считать, что смещения малы в сравнении с межатомными расстояниями , а силы взаимодействия между атомами - квазиупругие. Смещения описывают продольные колебания атомов вблизи положения их равновесия.

Найдем уравнения движения атомов. Учитывая взаимодействие лишь ближайших атомов (соседних), результирующие силы, действующие на выбранные нами атомы, равны:

,

где β- силовая постоянная, связанная с упругой постоянной. Согласно второму закону Ньютона, запишем уравнение движения:

, (6.3)

.

Колебания атомов с различными массами будут происходить с разными амплитудами, поэтому решение уравнения будем искать в виде:

; . (6.4)

Если подставить эти решения в систему (6.3), то получим

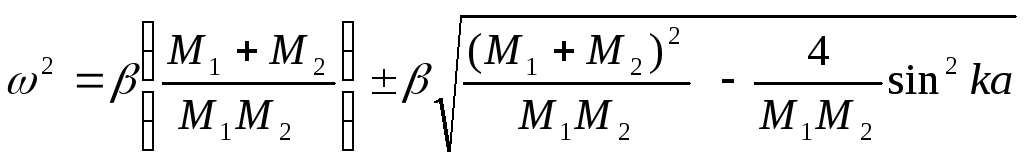
- каждому значению волнового числа κ соответствуют два значения ω, следовательно, и две моды колебаний типа (6.4). Возможные значенияkограничены соотношением:

.

При этом число допустимых неэквивалентных значений kв интервалеравноN - числу элементарных ячеек в цепочке. Так как каждому значениюkсоответствуют две моды колебаний, то полное число нормальных мод в интервалеравно числу степеней свободы в системе, т.е. 2N.

Решение задачи о колебаниях атомов двух сортов, таким образом, приводит к двум кривым зависимости , которые называются двумя ветвями закона дисперсии (см. рис.6.8).

Н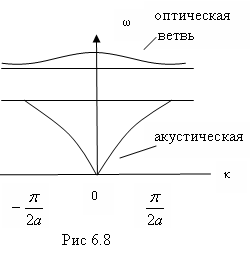ижнюю кривую называют акустической ветвью, верхнюю - оптической. Частота оптических колебаний больше частоты акустических колебаний.

Для оптической ветви:

,

для акустичeской:

.

Акустические колебания продольные, Частота стремится к нулю пропорционально k.

Длинноволновые оптические моды в ионных кристаллах могут взаимодействовать с электромагнитным излучением. При k=0 частота максимальна, с ростомkона уменьшается и при.

Таким образом, во всем интервале волновых чисел от 0 до в цепочке, состоящей из атомов двух сортов, происходит разделение колебаний на акустическую и оптическую ветви, при этом для акустических мод атомы обоих типов движутся в волне сжатия (в фазе). Для оптических мод колебаний соседние атомы движутся в противофазе.

Если рассматривать оптические колебания при малых значениях κ (длинные волны) и считать заряды атомов поочередно различными, то их колебания в противофазе вызовут смещения ионов, которые приведут к изменению электрического дипольного момента ячейки. В результате вдоль цепочки будет распространяться волна электрической поляризации с волновым числом k.