6.3.Колебания одноатомной линейной цепочки

Рассмотрим цепочку из Nодинаковых атомов с массойMи межатомным расстояниемa, атомы могут перемещаться вдоль прямой линии. Каждый атом в такой системе обладает одной степенью свободы. Эта модель хорошо описывается примитивной ячейкой Браве, в которой положение атомов определяется вектором трансляции, гдеn-целое число, указывающее положение равновесия атомов в цепочке.

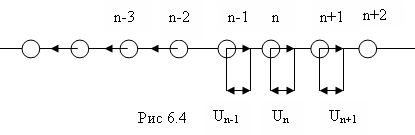
Будем считать, что в момент времени t=0 смещен атом с номеромn=0 от положения равновесия на расстояние(рис.6.4). Атомы связаны друг с другом, поэтому возбуждение распространится по цепочке в виде волны сжатия, и все остальные атомы сместятся от положения равновесия.

Пусть и_n(x, t) - смещение в какой-то момент времениtn-ого атома относительно его положения равновесия в точке с координатойx_n=na. Если смещения атомов из положений равновесия малы по сравнению с расстояниема, то силы межатомного взаимодействия можно считать квазиупругими, пропорциональными смещению. Атомы в цепочке как бы связаны между собой упругими пружинками, каждая из которых характеризуется упругой постояннойС, а смещениеu_nописывает колебания атома вблизи положения равновесия.

Найдем уравнение движения n-ого атома. Будем считать, что силы короткодействующие, и рассматриваемый атом взаимодействует только с (n+1) и (n-1) атомами. Взаимодействиеn-ого атома с другими (n-2,n+2 и т.д.) пренебрежительно мало. Наn-ный атом действуют квазиупругие силы, результирующая которых равна:

,

где β-силовая постоянная, которая связана с упругой постоянной.

Уравнение движенияn-ого атома:

, (6.2)

где M-масса атома.

Найдем нормальные моды колебаний, т.е. такие типы движения, при которых все атомы колеблются во времени с одной и той же частотой ω по законуexp(-ωt). Будем искать решение уравнения (6.2) в виде

,

здесь и₀определяет смещение атома с номеромn=0 в моментt=0,-волновое число;

ω- циклическая частота данной моды.

Из этого решения ясно, что вид нормальной моды полностью определяется заданием смещения единственного атома с номеромn=0. После подстановки этого решения в (6.2) имеем:

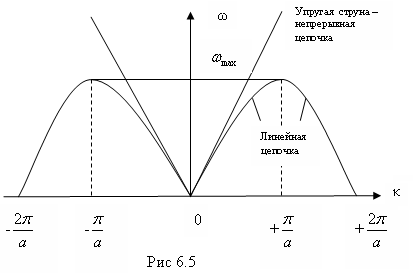
- каждому значению волнового числа k соответствует определенное значениеω², причемω²является четной функцией аргументаk. Дисперсионное соотношение для волн, распространяющихся в линейной цепочке из одинаковых атомов (рис.6.5) имеет вид:

.

Частота колебаний n-ого атома не зависит отn, т.е. все атомы цепочки колеблются с одинаковой частотойω, которая принимает максимальное значение при, т.е. при, при этом.

Таким образом, отличие дискретной цепочки от непрерывной состоит в том, что частота ωи волновое числоkне пропорциональны. Это связано с дисперсией волн. Короткие волны вследствие инерции, обусловленной массами частиц, распространяются медленнее, чем длинные волны. Наличие дисперсии волн проявляется в отклонении кривойот линейной зависимости, справедливой для упругой струны (прямая на рис.6.5). Цепочка из одинаковых атомов ведет себя в отношении распространения акустических волн как упругая струна только при.

Скорость распространения акустической волны вдоль дискретной цепочки в отличие от скорости распространения волны вдоль упругой струны зависит от длины волны:

.

Фазовая скорость упругой волны в среде с дискретной структурой равна

,

групповая скорость, где υ_зв- скорость звука в данной среде.

При малых значениях волнового числа k(рис.6.6) фазовая и групповая скорости совпадают и равны скорости звука: . Из рис.6.6 видно, что групповая скорость, с которой переносится энергия колебаний атомов в цепочке, для самых коротких длин волн, т.е. для , обращается в ноль. Это означает, что такие моды колебаний характеризуют в цепочке стоячие волны вида

,

которые являются результатом сложения двух бегущих волн с равными амплитудами, частотами и длинами, но распространяющихся в противоположных направлениях.

Состояние атомов дискретной цепочки описывается уравнением движения линейного гармонического осциллятора. Полная энергия такого осциллятора складывается из его кинетической и потенциальной энергий: , где– нормальная координата,М – масса осциллятора.

В квантовой механике гармонический осциллятор описывается оператором Гамильтона , где- оператор импульса,- оператор координаты.

Уравнение Шредингера для стационарных состояний имеет вид:

,

Решением уравнения Шредингера являются возможные (собственные) значения энергии:

,

n=0,1…-главное квантовое число. Энергия осциллятора имеет лишь дискретные значения.

Член представляет нулевую энергию. Он показывает, что даже приТ=0 К атомы не находятся в положениях равновесия, а совершают колебания.

Таким образом, полная тепловая энергия колебаний атомов в цепочке складывается из энергии нормальных колебаний, ведущих себя подобно линейным гармоническим осцилляторам с собственной частотой ω_κ .