1.3. Обозначение плоскостей и направлений в кристалле

Выберем систему координат с осями, совпадающими с тремя ребрами элементарной кристаллической сетки, начало координат находится в одном из узлов решетки, в котором пересекаются эти ребра, а осевые единицы соответствуют длине ребер кристаллической сетки (рис.1.3.). Масштаб по оси х равен длине ребра элементарной ячейки a; по y – b; по z – с. 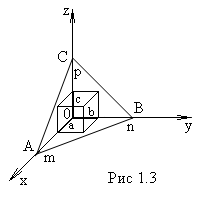Положение плоскости в пространстве определяется тремя точками. В выбранной системе координат в качестве трех таких точек берут точки пересечения заданной плоскости с осями координат.

Пусть узловая плоскость Sпересекает оси координат в точкахА,В,Си отсекает по осям отрезкиm,n,p, причемm=OA/a;n=OB/b;p=OC/c.Отношение обратных величин осевых отрезков имеет видh:k:=1/m:1/n:1/p,гдеh,k, -индексы Миллера. Для их нахождения отношение 1/m:1/n:1/pприводят к общему наименьшему знаменателю и отбрасывают его. Например, 1/m:1/n:1/p=1/5:1/2:1/7=14/70:35/70:10/70=14:35:10, т.е.h=14;k=35; =10. ПлоскостьSобозначают (14,35,10).

Е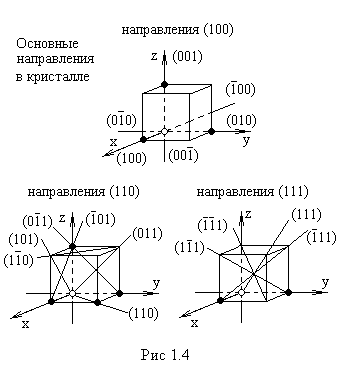сли плоскостьSпараллельна какой-либо оси, то соответствующий ей индексh,k, равен нулю, и если индекс отрицательный, знак “минус” ставится над ним: (1,,3).

Некоторые плоскости, различающиеся по индексам Миллера, являются эквивалентными (например, в кубе грани (1 0 0 ), ( 0 1 0 ), (0 0 1), (0 0), (00), (0 0) ). Эти плоскости могут быть совмещены друг с другом при повороте вокруг одной из осей координат на угол, кратный 90⁰. Эти плоскости обладают одинаковой структурой в расположении узлов решетки, и, следовательно, одинаковыми физическими свойствами. Семейство эквивалентных плоскостей обозначается фигурными скобками: {100}. Плоскости (hk) и () неэквивалентны, поэтому семейство включает в себя 6 (aне 12) различных систем плоскостей (рис.1.4).

Индексы направления в кристалле представляют собой набор наименьших чисел u,v,w, отношение которых друг к другу равно отношению проекций вектора, параллельного заданному направлению, на кристаллографические оси координат (рис.2). Эти индексы заключаются в квадратные скобки [uvw]. Семейство эквивалентных направлений обозначается ломаными скобками <uvw>.

С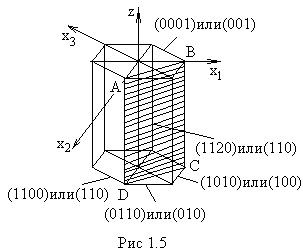имволика Миллера применяется для всех кристаллографических систем, кроме гексагональной. Кристаллы гексагональной системы описываются с помощью четырех координатных осейx₁,x₂,x₃,z. Осиx₁,x_2, x₃имеют одинаковый масштаб, угол между ними 120⁰. Осьz перпендикулярна к плоскости (x₁,x₂,x₃. В гексагональной системе применяются индексы Миллера - Браве. Принцип определения этих индексов в тот же : если осевые отрезкиm, n, q, p,то индексы Миллера - Браве:h:k:i: =1/m:1/n:1/q:1/p.

При этом =-(h+k). Это можно показать геометрически (угол между (x₁,x₂); (x₂,x₃); (x₃,x₁) равен 120⁰). Это дает возможность не писать третий индекс и свести индексы Миллера – Браве к индексам Миллера (рис.1.5).

1.4.Обратная решетка

Обратная решетка не является решеткой в том обычном смысле, который мы вкладываем при определении пространственной решетки кристалла.

Обратной решетки не существует в кристалле, она представляет собой удобную абстракцию, позволяющую математически просто и точно описывать условия, в которых протекает то или иное явление в твердом кристаллическом теле.

Прямая и обратная решетки взаимно сопряжены. Решетка, обратная к обратной, есть просто исходная прямая решетка. Каждый узел [[hk]]* обратной решетки соответствует семейству параллельных плоскостей (hk) прямой решетки. При этом обратная решетка строится по отношению к конкретной решетке Браве и сама является решеткой Браве. Так, для простой кубической ячейки Браве обратной решеткой является решетка, описываемая простой кубической элементарной ячейкой со стороной 1/а, гдеа- параметр прямой ячейки. Обратная к гранецентрированной есть объемно- центрированная решетка, а прямой объемно- центрированной решетке соответствует обратная гранецентрированная. Вектор обратной решеткиперпендикулярен к плоскости (h,k, ) и по модулю равен 1/d_hkl, гдеd_hkl- межплоскостное расстояние в системе эквивалентных плоскостей {h,k, }прямой решетки.