
4.3.Потенциальное поле сил. Консервативные силы
Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица находится в поле сил. Например, вблизи поверхности Земли частица находится в поле силы тяжести.
 В электрическом
поле неподвижного точечного заряда
В электрическом
поле неподвижного точечного заряда
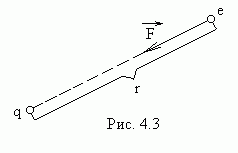
![]() на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд
на заряженную частицу действует поле,
характерное тем, что направление силы,
действующей на частицу в любой точке
пространства, проходит через неподвижный
центр (заряд![]() ),
а величина силы зависит только от
расстояния до этого центра:
),
а величина силы зависит только от
расстояния до этого центра:![]() .
Такое поле называется центральным
(рис.4.3).
.
Такое поле называется центральным
(рис.4.3).
Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению, поле называется однородным.
Силовое поле,
которое можно описать с помощью функции
![]() такой, что
такой, что
![]() (4.6)
(4.6)
называется
потенциальным. Функция
![]() называется потенциальной функцией или
потенциалом. Если поле не изменяется
со временем, оно называется стационарным,
в этом случае
называется потенциальной функцией или
потенциалом. Если поле не изменяется
со временем, оно называется стационарным,
в этом случае![]() .
.
Добавление к
функции
![]() произвольной постоянной величины не
изменяет значений
произвольной постоянной величины не
изменяет значений
![]() ,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной
,
вычисляемых по формулам (4.6) . Поэтому
потенциальная функция определяется с
точностью до произвольной аддитивной
постоянной. Однако при фиксированном
значении этой постоянной
![]() становится однозначной функцией
координат и времени.
становится однозначной функцией
координат и времени.
Вектор с
компонентами
![]() ,
где
,
где![]() -
скалярная функция координат, называется
градиентом функции
-
скалярная функция координат, называется
градиентом функции![]() и обозначается
и обозначается![]() либо
либо![]() (
(![]() называется оператором набла,
называется оператором набла,![]() читается:
«набла фи» или «градиент фи»). Из
определения градиента следует, что
читается:
«набла фи» или «градиент фи»). Из
определения градиента следует, что
![]() ,
поэтому в случае потенциального силового
поля имеем:
,
поэтому в случае потенциального силового
поля имеем:
![]() .
(4.7)
.
(4.7)
Работа силы, удовлетворяющей условию (4.7), равна
![]()
![]() ,
(4.8)
,
(4.8)
т.е. представляет
собой полный дифференциал функции
![]() .
Проинтегрировав выражение (4.8) по
некоторой траектории от точки 1 до точки
2, получаем:
.
Проинтегрировав выражение (4.8) по
некоторой траектории от точки 1 до точки
2, получаем:
![]() .
(4.9)
.
(4.9)
Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольной. Таким образом, работа, совершаемая над частицей силами стационарного потенциального поля, не зависит от пути, по которому двигалась частица, а определяется только начальным и конечным положениями частицы в пространстве.
 Силы, работа
которых не зависит от пути, по которому
частица переходит из одного положения
в другое, называются консервативными.
Следовательно, силы, действующие на
частицу в стационарном потенциальном
поле, являются консервативными.
Силы, работа
которых не зависит от пути, по которому
частица переходит из одного положения
в другое, называются консервативными.
Следовательно, силы, действующие на
частицу в стационарном потенциальном
поле, являются консервативными.
Из независимости
работы консервативных сил от пути
вытекает, что работа таких сил на
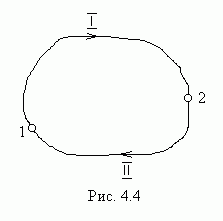
замкнутом пути равна нулю. Чтобы доказать
это, разобьем произвольный замкнутый
путь (рис.4.4) на две части: путь 1, по
которому частица переходит из точки 1
в точку 2, и путь
![]() ,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
,
по которому частица переходит из точки
2 в точку 1. При этом точки 1 и 2 выбраны
произвольно.
Работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков:
![]() .
(4.10)
.
(4.10)
Очевидно, работы
![]() и
и
![]() отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене
отличаются
только знаком. Действительно, изменение
направления движения на обратное
приводит к замене
![]() на
-
на
-![]() ,
поэтому значение интеграла
,
поэтому значение интеграла![]() изменяет знак на обратный.
изменяет знак на обратный.
Поэтому равенство
(4.10) можно записать в виде:
![]() .Так
как работа не зависит от пути, то
.Так
как работа не зависит от пути, то
![]() =
-
=
-
![]() ,
и
,
и
![]() .
.
Кроме консервативных сил существуют неконсервативные силы. К ним относятся диссипативные силы, переводящие механическую энергию во внутреннюю ( это силы трения, сопротивления среды), а также гироскопические силы, перпендикулярные скорости ( сила Кореолиса, сила Лоренца), работа которых всегда равна нулю. Для неконсервативных сил соотношение (4.7) не выполняется.
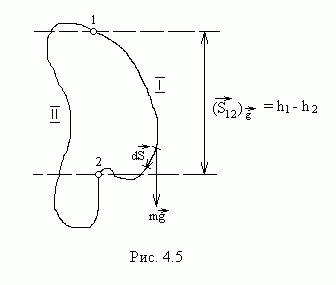 Докажем, что сила
тяжести является консервативной. Эта
сила в любой точке имеет одинаковые
величину и направление – вниз по
вертикали (рис.4.5). Поэтому, независимо
от того, по какому из путей 1 или II
движется частица, работа определяется
выражением:
Докажем, что сила
тяжести является консервативной. Эта
сила в любой точке имеет одинаковые
величину и направление – вниз по
вертикали (рис.4.5). Поэтому, независимо
от того, по какому из путей 1 или II
движется частица, работа определяется
выражением:
![]()
Из рис.4.5 видно,
что проекция вектора
![]() на направление
на направление
![]() равна разности высот
равна разности высот
![]() .
Тогда работа
.
Тогда работа
![]()
Это выражение не зависит от пути, следовательно, сила тяжести консервативна.
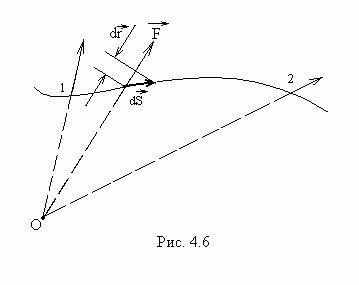 Силы, действующие
на частицу в центральном поле, также
консервативны (рис.4.6). Элементарная
работа центральной силы на пути
Силы, действующие
на частицу в центральном поле, также
консервативны (рис.4.6). Элементарная
работа центральной силы на пути
![]() равна
равна![]() .
Проекция
.
Проекция![]() на направление силы в данном месте –
это проекция на направление радиуса-вектора
на направление силы в данном месте –
это проекция на направление радиуса-вектора![]() , она равна приращению расстояния частицы
до центра силового поля О:
, она равна приращению расстояния частицы
до центра силового поля О:
![]() .
Работа на всем пути
.
Работа на всем пути
![]()
Это выражение
зависит только от вида функции
![]() и от значений
и от значений![]() и
и![]() .
От вида траектории оно не зависит,
следовательно, центральная сила
консервативна.
.
От вида траектории оно не зависит,
следовательно, центральная сила
консервативна.
4.4. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВО ВНЕШНЕМ ПОЛЕ СИЛ
Из выражения (4.9) следует, что работа равна приращению потенциальной функции, и эта работа идет на приращение кинетической энергии частицы, как показывает (4.5). Таким образом,
![]() .
(4.11)
.
(4.11)
Перейдем от
функции
![]() к
функции
к
функции![]() ,
связанной с
,
связанной с![]() соотношением
соотношением
![]() .
(4.12)
.
(4.12)
Тогда из (4.11)
получаем:
![]() ,
или
,
или![]() .
.
Полученный результат
означает, что величина
![]() для частицы, находящейся в поле
консервативных сил, остается постоянной,
т.е. является интегралом движения.
Функция
для частицы, находящейся в поле
консервативных сил, остается постоянной,
т.е. является интегралом движения.
Функция![]() называется потенциальной энергией
частицы во внешнем поле сил. Таким
образом, потенциальная энергия
характеризует взаимодействие частицы
с полем сил и зависит от положения
частицы в этом поле, т.е. от координат.
Величину
называется потенциальной энергией
частицы во внешнем поле сил. Таким
образом, потенциальная энергия
характеризует взаимодействие частицы
с полем сил и зависит от положения
частицы в этом поле, т.е. от координат.
Величину![]() ,
равную сумме кинетической и потенциальной
энергии, называют полной механической
энергией частицы.
,
равную сумме кинетической и потенциальной
энергии, называют полной механической
энергией частицы.
Из выражения (4.9) с учетом (4.12) получаем
![]()
-работа, совершаемая над частицей силами консервативного поля, равна убыли потенциальной энергии частицы, т.е. работа совершается за счет запаса потенциальной энергии.
Выражение (4.7) с учетом (4.12) принимает вид
![]()
–сила, действующая на частицу в стационарном поле сил, равна градиенту потенциальной энергии частицы в этом поле, взятому с обратным знаком.
Пусть на частицу,
кроме сил стационарного потенциального
поля, действует также неконсервативная
сила
![]() .
Тогда при переходе частицы из точки 1 в
точку 2 над ней будет совершаться работа
.
Тогда при переходе частицы из точки 1 в
точку 2 над ней будет совершаться работа![]() ,гд
,гд![]() е
е![]() - работа неконсервативной силы. Работа
консервативных сил равна убыли
потенциальной энергии. Тогда
- работа неконсервативной силы. Работа
консервативных сил равна убыли
потенциальной энергии. Тогда
![]() .
.
Суммарная работа
всех приложенных к частице сил идет на
приращение ее кинетической энергии:
![]() ,
или
,
или
![]()
-работа неконсервативных сил затрачивается на приращение полной механической энергии частицы.
Потенциальная
энергия, как и потенциальная функция,
определяется с точностью до произвольной
аддитивной постоянной. Однако, это не
имеет значения, так как во все функции
входит либо разность значений потенциальной
энергии, либо ее производные. В каждой
конкретной задаче выбирается начало
отсчета потенциальной энергии, от
которого ведут расчет энергии в других
положениях. Поэтому
![]() может
иметь как положительные, так и отрицательные
значения.
может
иметь как положительные, так и отрицательные
значения.
Конкретный вид
функции
![]() зависит
от характера силового поля. В поле
тяжести
зависит
от характера силового поля. В поле
тяжести![]() ,
где
,
где![]() отсчитывается
от произвольного уровня.
отсчитывается
от произвольного уровня.
Рассмотрим
систему, состоящую из![]() невзаимодействующих между собой частиц,
находящихся в поле консервативных сил.
Каждая из частиц обладает кинетической
невзаимодействующих между собой частиц,
находящихся в поле консервативных сил.
Каждая из частиц обладает кинетической![]() и потенциальной энергией
и потенциальной энергией![]() номер
частицы, тогда для каждой частицы можно
записать
номер
частицы, тогда для каждой частицы можно
записать
![]()
Просуммировав эти выражения для всех частиц, получаем
![]()
- полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной.
4.5.ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ
 Рассмотрим
замкнутую систему, состоящую из двух
взаимодействующих частиц (рис.4.7). Введем
вектор
Рассмотрим
замкнутую систему, состоящую из двух
взаимодействующих частиц (рис.4.7). Введем
вектор
![]() ,
где
,
где![]() и
и![]() -
радиус-векторы частиц. Расстояние между
частицами равно модулю этого вектора.
Будем считать, что силы взаимодействия
частиц
-
радиус-векторы частиц. Расстояние между
частицами равно модулю этого вектора.
Будем считать, что силы взаимодействия
частиц![]() и
и![]() зависят только от расстояния
зависят только от расстояния![]() между ними, и направлены вдоль прямой,
соединяющей частицы:
между ними, и направлены вдоль прямой,
соединяющей частицы:
![]() ,
(4.13)
,
(4.13)
г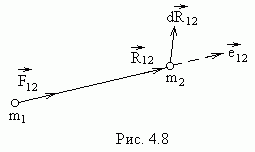 де
де![]() - некоторая функция
- некоторая функция![]() ,
,![]() -
орт вектора
-
орт вектора![]() (рис.4.8).
По третьему закону Ньютона
(рис.4.8).
По третьему закону Ньютона![]() =
=
![]() .
Уравнения движения частиц
.
Уравнения движения частиц
![]() .
.
Умножим первое
уравнение на
![]() ,
второе – на
,
второе – на![]() и сложим:
и сложим:
![]() .
(4.14)
.
(4.14)
Левая часть этого
выражения представляет собой приращение
кинетической энергии системы за время
![]() , а правая часть – работу внутренних
сил за то же время:
, а правая часть – работу внутренних
сил за то же время:
![]() .
.
Подставив в это выражение формулу (4.13), получаем
![]() .
.
Из рис.4.7 видно,
что скалярное произведение
![]() равно приращению расстояния между
частицами. Тогда
равно приращению расстояния между
частицами. Тогда
![]() .
.
Выражение![]() есть
приращение некоторой функции от
есть
приращение некоторой функции от![]() :
:
![]() .
.
Следовательно,![]() и
выражение (4.14) можно представить в виде:
и
выражение (4.14) можно представить в виде:
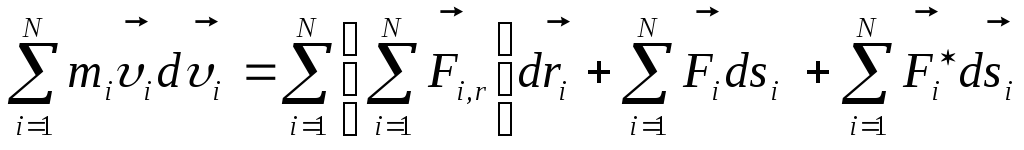 .
.
![]() или
или
![]() таким
образом, величина
таким
образом, величина![]() для
замкнутой системы сохраняется. Функция
для
замкнутой системы сохраняется. Функция![]() представляет собой потенциальную
энергию взаимодействия. Она зависит от
расстояния между частицами. Работа
внутренних сил
представляет собой потенциальную
энергию взаимодействия. Она зависит от
расстояния между частицами. Работа
внутренних сил
Т![]() .е.
не зависит от путей, по которым перемещались
частицы, а определяется только начальными
и конечными расстояниями между частицами.
Таким образом, силы взаимодействия вида
(4.13) являются консервативными.
.е.
не зависит от путей, по которым перемещались
частицы, а определяется только начальными
и конечными расстояниями между частицами.
Таким образом, силы взаимодействия вида
(4.13) являются консервативными.
