7. Перемещением точки за промежуток времени называется вектор, проведенный из начального положения точки (в момент времени) в ее конечное положение ( в момент времени).

Если точка совершает последовательно два перемещения и, торезультирующее перемещение равно векторной сумме (рис.1.3):

Вектор перемещения направлен вдоль хорды, стягивающей соответствующий участок траектории точки, из положения движущейся точки в момент времени в её положение в момент времени. Поэтому во всех случаях, кроме прямолинейного движения точки, модуль вектора перемещения меньше длины пути точки за тот же самый промежуток времени.

1.2.Скорость

1. В физике под скоростью понимают векторную величину, характеризующую быстроту перемещения материальной точки по траектории и направление движения в каждый момент времени.

Р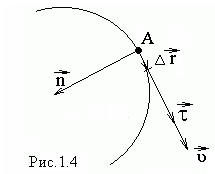азобьем траекторию на бесконечно малые участки длины(рис.1.4), каждому из этих участков сопоставим бесконечно малое перемещение.

Разделив это перемещение на соответствующий промежуток времени , получиммгновенную скорость в данной точке траектории:

. (1.3)

Таким образом, скорость есть первая производная радиус-вектора точки по времени.

Перемещение совпадает с бесконечно малым элементом траектории, следовательно вектор направлен по касательной к траектории ( рис.1.4).

Разложив вектор скорости по базису системы координат, получаем:

,

где проекции вектора на координатные оси :

Модуль вектора скорости равен:

.

Средней скоростью точки в промежутке времени от t до t +Δt называется вектор , равный отношению приращения Δr радиуса-вектора точки за этот промежуток времени к его продолжительности Δt:

Средняя скорость направлена также как и вектор перемещения , т. е. вдоль хорды, стягивающей соответствующий участок траектории.

2. Движение называется равномерным, если вектор скорости остается постоянным по величине и направлению.

В противном случае говорят о переменном движении.

В соответствии с формулой (1.3), элементарное перемещение материальной точки :

.

Тогда перемещение из положения 1 в положение 2 (рис.1.2) равно интегралу:

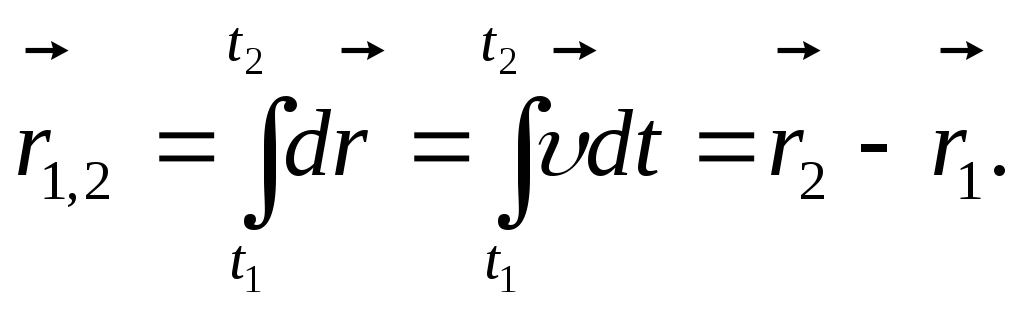
Пройденный путь определяется выражением:

.

Если точка движется равномерно и прямолинейно со скоростью вдоль оси ОХ, то зависимость координаты от времени имеет вид:

3. Если модуль вектора скорости точки изменяется с течением времени, то такое движение точки называется неравномерным.

Среднее значение модуля скорости за время от до равно:

Средний вектор скорости : .

1.3.Ускорение

1. Быстрота изменения вектора скорости называетсяускорением материальной точки и определяется производной вектора по времени:

. (1.5)

Cпроектируем это выражение на координатные оси:

.

Подставив в формулу (1.5) выражение (1.4), получаем:

.

Продифференцировав, имеем:

.

Следовательно, вектор можно представить в виде суммы двух взаимно перпендикулярных составляющих(рис.1.6).

Первая направлена по касательной к траекториии называетсятангенциальным или касательным ускорением:

. (1.6)

Вторая составляющая направлена по , т.е. перпендикулярно касательной, по нормали к траектории, и называется нормальным ускорением:

.

Исследуем свойства обеих составляющих, ограничившись случаем плоского движения.

1) тангенциальное ускорение точки характеризует быстроту изменения модуля её скорости

Модуль тангенциального ускорения, как следует из (1.6), равен .

• Если 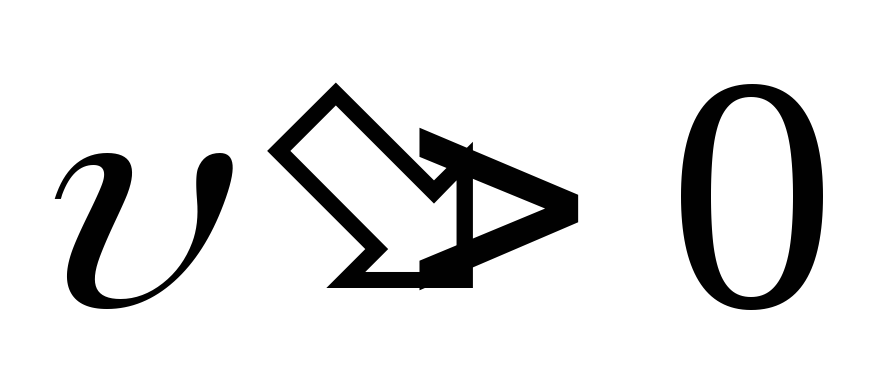(скорость растет по величине), вектор направлен в ту же сторону, что и( т.е. в ту же сторону, что и), проекция ускорения на направление скорости положительная величина - ускоренное движение.

• Если (скорость со временем уменьшается), векторы инаправлены противоположно, проекция ускорения на направление скорости отрицательная величина - замедленное движение.

• При равнопеременном движении .

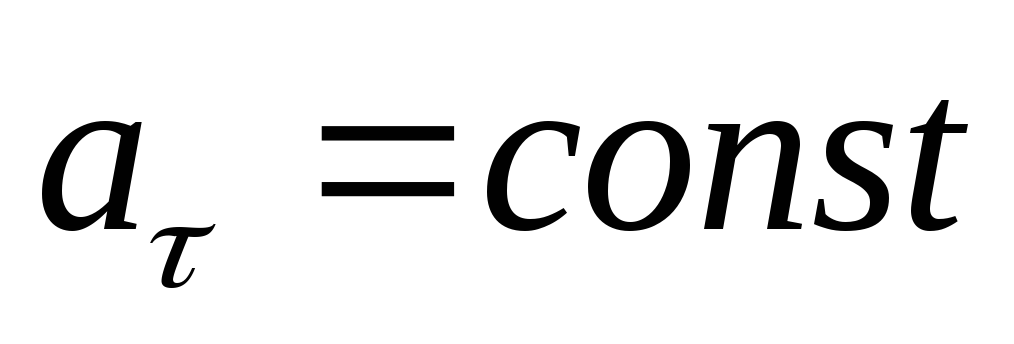Равноускоренное движение >0, равнозамедленное - <0

• При равномерном движении .

2) Нормальное ускорение определяется величиной , характеризует быстроту изменения направления вектора скорости точек.

Эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.

Направлено всегда к центру кривизны траектории.

При равномерном движении точки по окружности , но векторизменяется, так как направление векторовв разных точках окружности разные.

2.Степень искривления плоской кривой характеризуется кривизной С, которая определяется выражением

где –угол между касательными к кривой в точках, отстоящих друг от друга на расстояние(рис.1.7).

Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой.

Величина, обратная кривизне С, называется радиусом кривизны в данной точке

Радиус кривизныпредставляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке.

Центр такой окружности называется центром кривизны для данной точки кривой.

Радиус и центр кривизны в точке 1 (рис.1.7) определим следующим образом.

- Возьмем вблизи точки 1 точку 1.

- Построим в этих точках касательные и, перпендикуляры к которым пересекутся в некоторой точкеО. При этом для кривой, не являющейся окружностью, расстояния  и  несколько отличаются друг от друга.

- Если точку 1 приближать к точке 1, пересечение перпендикуляров O будет перемещаться вдоль прямой  и в пределе окажется в некоторой точке О. Эта точка и будет центром кривизны для точки 1.

- Расстояния R и R будут стремиться к общему пределу , равному радиусу кривизны.

Как известно из математики, (1.7)

Здесь – орт нормали к траектории, направленный в сторону поворота векторапри движении частицы по траектории.

Величину можно связать с радиусом кривизны траектории и скоростью частицы.

Из рис. 1.7 следует, что

где - угол поворота вектораза время(совпадающий с углом между перпендикулярами и ),

- средняя скорость на пути .

Отсюда .

В пределе при  0 приближенное равенство станет строгим, средняя скорость превратится в мгновенную скоростьв точке 1,- в радиус кривизны .

В результате получится равенство (1.8)

- быстрота поворота вектора скорости пропорциональна кривизне траектории и скорости перемещения частицы по траектории.

Подставив (1.7) в формулу (1.8), получим ,

тогда нормальное ускорение равно .