Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

ГОУ ВПО Рыбинская государственная авиационная технологическая

академия им. П.А. Соловьева

КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ

УТВЕРЖДЕНО

на заседании методического

семинара кафедры ОиТФ

« » _________ 2007 г.

Зав.каф. Пиралишвили Ш.А.

Лаборатория «Волновая механика»

ЛАБОРАТОРНАЯ РАБОТА№ ВМ – 7

ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ ЯВЛЕНИЙ

В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Нормоконтроль	Автор: к. т. н., доцент Суворова З. В.
____________	___________________
	Рецензент: к. ф–м. н., доцент Шалагина Е.В.
	___________________

Рыбинск 2007

ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ

1. Убедитесь в присоединении заземляющих проводов к корпусам осциллографа, генератора.

2. Включать приборы только с разрешения преподавателя.

3. Не производить никаких переключений на лицевой панели осциллографа и генератора, кроме тех, что указаны в настоящем руководстве.

4. При обнаружении признаков неисправности (искрение, запах дыма) отключить приборы от сети и известить преподавателя.

При работе соблюдать нормы электробезопасности согласно инструкции №170, определяющей правила работы в лаборатории волновой механики!

ЦЕЛЬ РАБОТЫ: наблюдение резонанса в цепи переменного тока, установление критериев его возникновения в параллельном и последовательном контурах.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: блок исследуемых колебательных контуров с переключателем; звуковой генератор и осциллограф.

1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Рис.1

_{Идеальный колебательный контур, состоящий из индуктивности L и ёмкости С, представляет собой линейный гармонический осциллятор, обладающий одной степенью свободы (рис. 1). Состояние такого контура в любой момент времени может быть однозначно описано единственным параметром – зарядом q на конденсаторе. 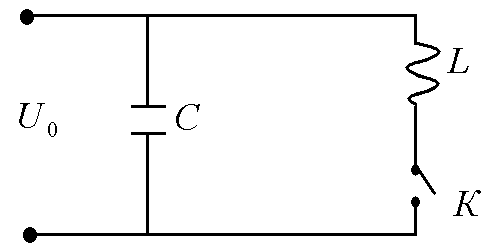Если сопротивление контура равно нулю, R =0, то при замыкании индуктивности на предварительно заряженный конденсатор с зарядом в контуре возникают гармонические колебания.}

_{Падение напряжения на конденсаторе . При замыкании цепи в индуктивности возникает ЭДС индукции где ток , поэтому .}

_{Согласно второму правилу Кирхгофа то есть , или}

Рис. 2

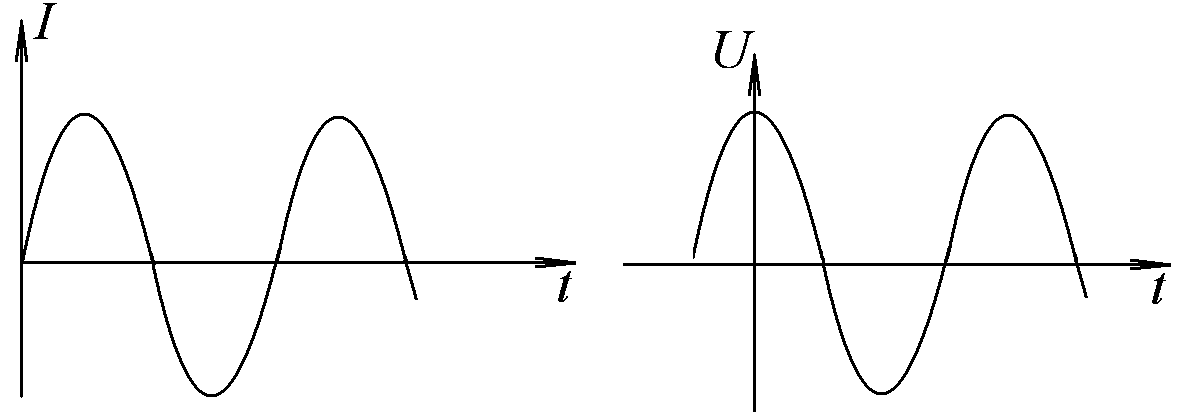
_{Это уравнение является уравнением свободных гармонических колебаний с циклической частотой Его решение , где – заряд конденсатора в момент времени t = 0.}

_{Для тока в катушке имеем:}

_{–сдвиг фаз между током в контуре и напряжением на конденсаторе составляет π/2, ток опережает по фазе напряжения на конденсаторе на π/2 (рис.2).}

_{Напряжение на конденсаторе меняется по закону:}

_{При колебаниях происходит периодический переход электрической энергии конденсатора в магнитную энергию катушки . При этом полная электромагнитная энергия сохраняется.}

Рис. 3

_{Всякий реальный контур обладает активным сопротивлением. Электромагнитная энергия в контуре постепенно расходуется в этом сопротивлении на нагревание проводника, вследствие чего колебания затухают. По второму правилу Кирхгофа для цепи на рис.3 имеем:}

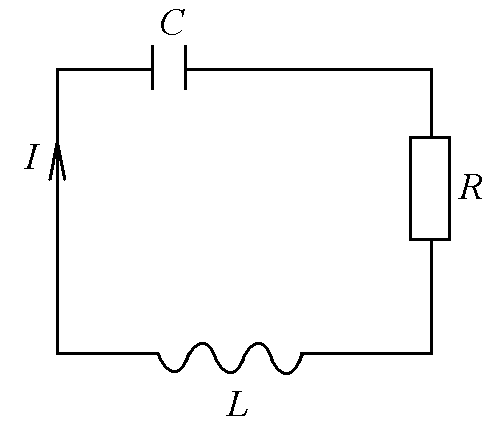
Разделим это уравнение на L и подставим,

_{Учитывая, что , и обозначив , получаем}

_{– дифференциальное уравнение затухающих колебаний.}

_{При , т.е. при (– коэффициент затухания), решение этого уравнения имеет вид}

_{, (1)}

_{где . Подставив и , получаем Таким образом, частота затухающих колебаний меньше собственной частоты .}

_{Для определения напряжения на конденсаторе разделим (1) на С, имеем}

_{Чтобы найти закон изменения силы тока, продифференцируем (1) по времени:}

_{Обозначим тогда}

Рис. 4

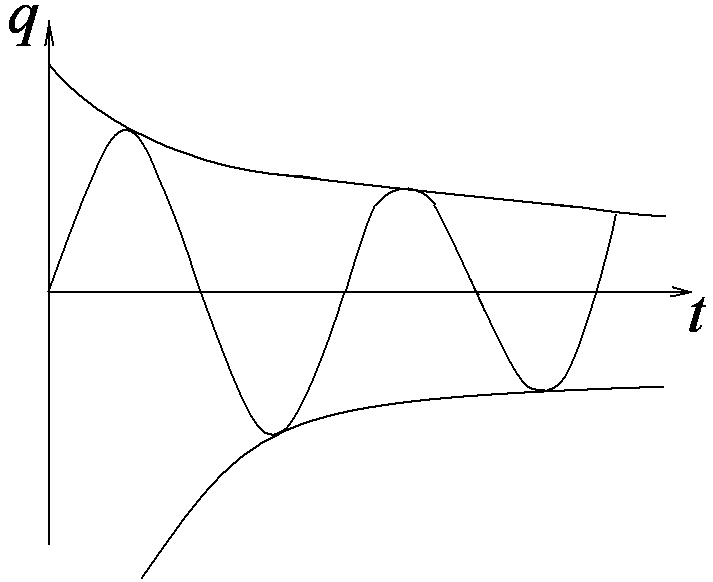
_{Так как то – при наличии в контуре активного сопротивления сила тока опережает по фазе напряжение на конденсаторе более, чем на}

_{График функции представлен на рис.4.}

_{Логарифмический декремент затухания Он определяется параметрами контура R, L, C и является характеристикой этого контура.}

_{Если затухание невелико , то и Добротность контура в случае слабого затухания}

_{При слабом затухании добротность контура пропорциональна отношению энергии, запасённой в контуре в данный момент, к убыли этой энергии за один период. Действительно, амплитуда силы тока в контуре убывает по закону . Энергия W, запасённая в контуре, пропорциональна квадрату амплитуды силы тока, следовательно W убывает по закону . Относительное уменьшение за период равно:}

_{При незначительном затухании <<1 и можно считать ≈1-2. Тогда добротность .}

_{При частота становится комплексным числом, и происходит апериодический процесс разрядки конденсатора. Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим,}

_{Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС или подать на контур переменное напряжение (рис.5).}

Рис. 5

_{Цепь, в которой последовательно с ЭДС включены сопротивление R, индуктивность L и конденсатор С, называется последовательным колебательным контуром. Рассмотрим процессы в этом контуре.}

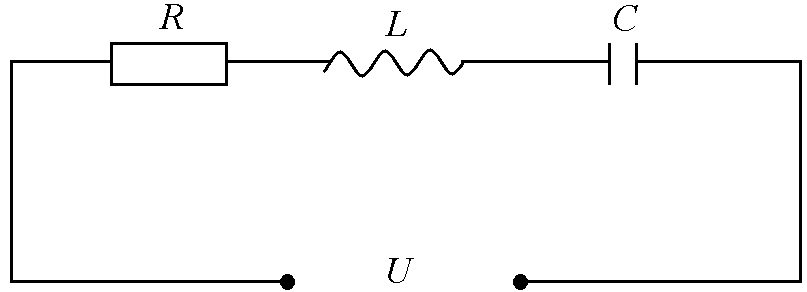
_{По второму правилу Кирхгофа}

_{или . Разделив на L, получаем уравнение вынужденных колебаний}

₍₂₎

_{Частное решение этого уравнения}

₍₃₎

_{где 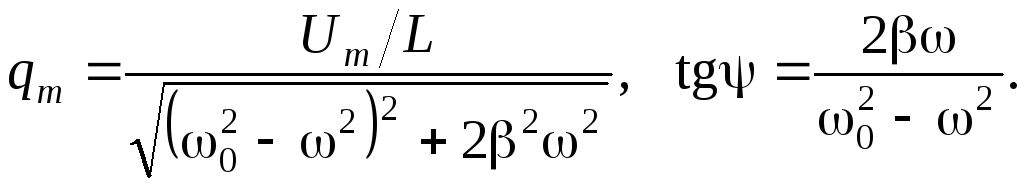Подставим и :}

_{Общее решение получится, если к частному решению (3) прибавить общее решение однородного дифференциального уравнения, которое было получено ранее. Оно содержит множитель , который очень быстро убывает, и при прошествии достаточно большого времени им можно пренебречь. Таким образом, установившиеся вынужденные электромагнитные колебания в контуре описываются уравнением (3).}

_{Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (3) по времени:}

_{где – сдвиг фаз между током и приложенным напряжением. Тогда}

_{Из этого выражения следует, что ток отстает по фазе от напряжения () при , и опережает напряжение () при . Для силы тока можно записать}

_{. (4)}

_{Представим соотношение (2) в виде:. Произведение – падение напряжения на активном сопротивлении; – падение напряжения на конденсаторе; – напряжение на индуктивности; тогда можно записать}

_{. (5)}

_{Таким образом, сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.}

_{Согласно (4) – напряжение на активном сопротивлении совпадает по фазе с током в контуре.}

_{Для напряжения на конденсаторе, подставив (3), имеем – напряжение на ёмкости отстаёт от силы тока на π/2.}

_{Напряжение на индуктивности}

_,

_{где , – напряжение на индуктивности опережает ток на π/2.}

_{Фазовые соотношения можно представить наглядно с помощью векторной диаграммы. Действительно, гармонические колебания можно задать с помощью вектора, длина которого равна амплитуде колебаний , а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 6).}

Рис. 6

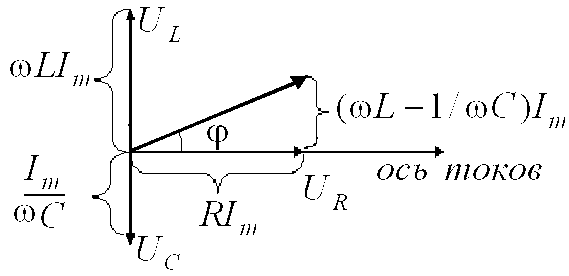
_{совпадает по фазе с током, – отстаёт на π/2), – опережает на π/2. Векторы , , в сумме дают , причём U определяется выражением (5).}

_{При определенной частоте внешнего воздействия в контуре наступает резонанс. Резонансная частота для напряжения на конденсаторе и для заряда q равна:}

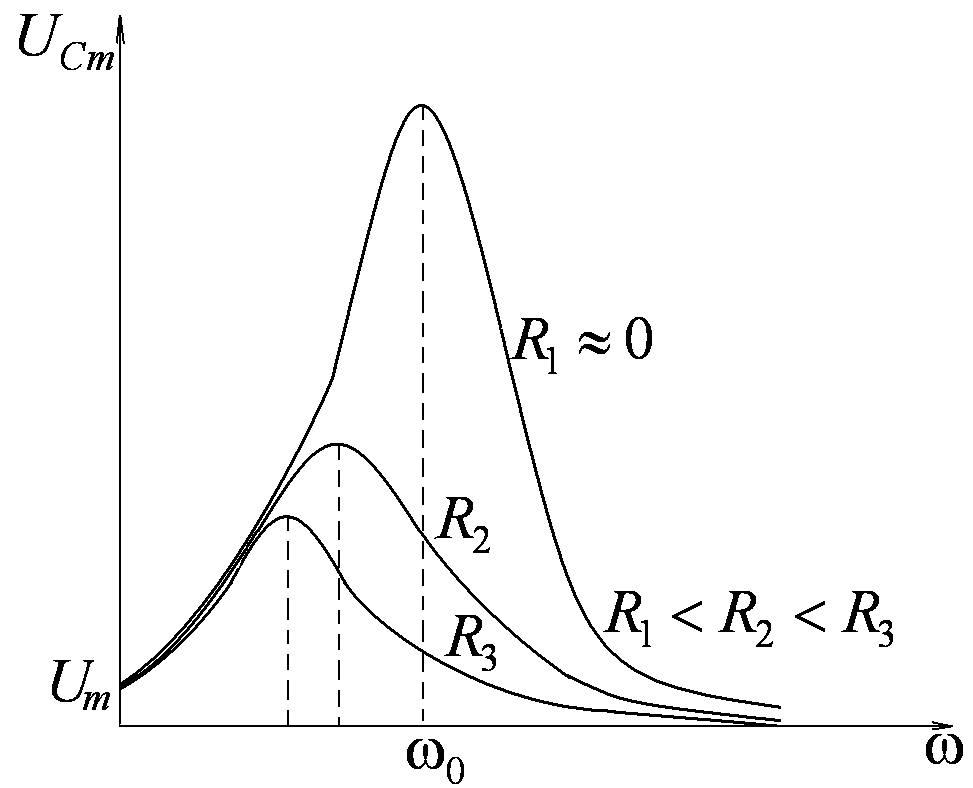
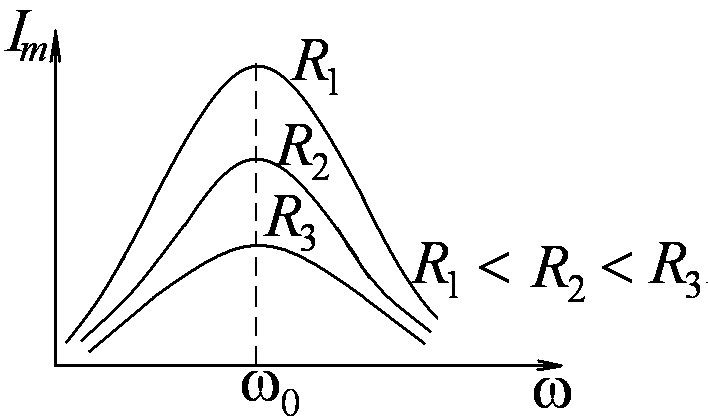
_{Резонансные кривые для имеют вид, представленный на рис.7. Все резонансные частоты . При ω→0 резонансные кривые сходятся в одной точке – это напряжение на конденсаторе при подключении его к источнику постоянного напряжения . Максимум при резонансе тем острее и выше, чем меньше затухание β=R/2L, то есть чем меньше R и больше L. Ход резонансной кривой аналогичен резонансной кривой при механических колебаниях.}

Рис. 7

_{Резонансные кривые для тока приведены на рис. 8.}

_{Амплитуда силы тока имеет максимальные значения, когда , то есть резонансная частота для силы тока совпадает с собственной частотой колебаний контура:}

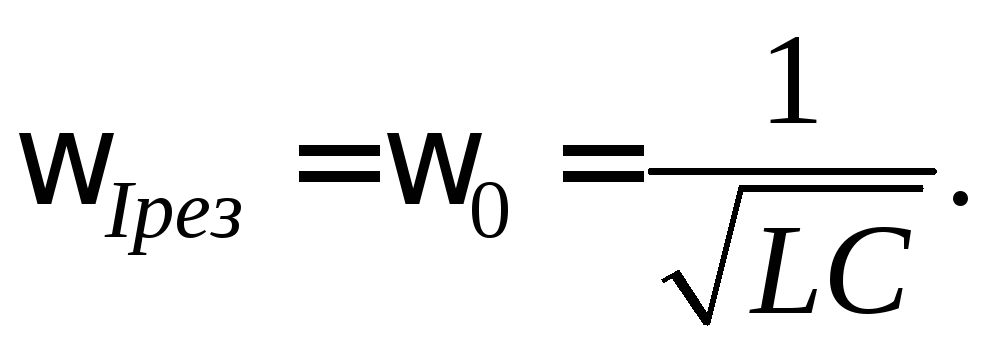
Рис. 8

_{При ω→0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.}

_{При малом затухании () резонансную частоту для напряжения можно считать равной . Тогда отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения равно:}

_{– то есть добротность контура показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.}

_{Итак, при резонансе 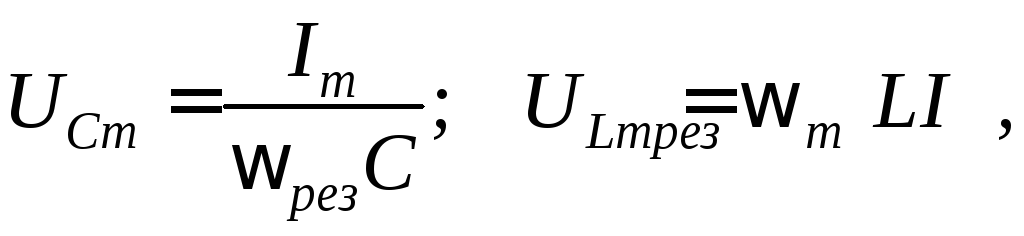причём поэтому}

– амплитуды напряжений на ёмкости и индуктивности равны между собой, но противоположны по фазе. Поэтому напряжения на ёмкости и индуктивности компенсируют друг друга, и цепь ведёт себя как цепь только с активным сопротивлением. Вся энергия, приложенная к контуру, идёт на Ленц-Джоулево тепло. Ток в цепи достигает максимального значения. Это резонанс напряжений – индуктивного и емкостного.

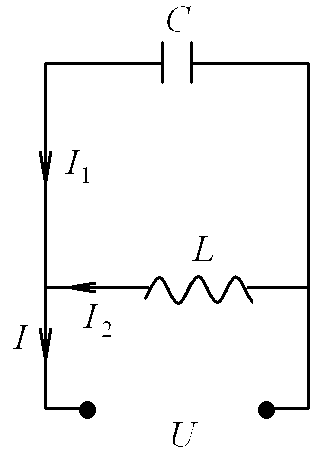
Рассмотрим колебательный контур, в котором индуктивность L и ёмкостьСсоединены параллельно (рис. 9).

Рис. 9

Будем считать активное сопротивление близким к нулю,R ≈ 0. Для амплитуд напряжений на индуктивности и ёмкости имеем:

По второму правилу Кирхгофа токиив каждый момент времени находятся в противофазе, поэтому

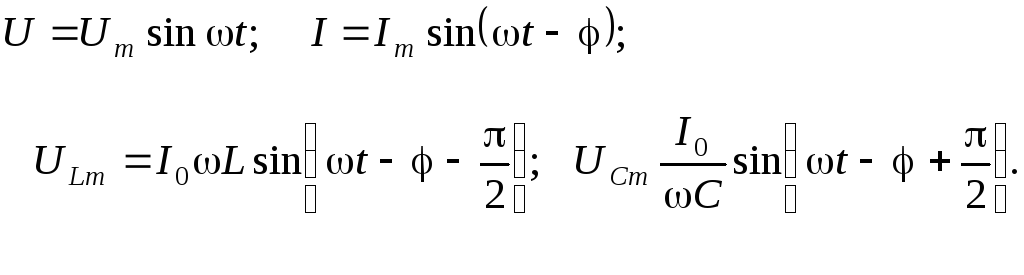
Ток в неразветвлённой цепи равен , или

.

При 1/ωL=ωCтокI = 0. Условие резонанса токов– частота колебаний равна собственной:

Установившиеся вынужденные колебания можно рассматривать как протекание в цепи, обладающей ёмкостью, индуктивностью и активным сопротивлением, переменного тока, который обусловлен переменным напряжением:

.

Ток изменяется по закону амплитуда тока

Ток отстаёт от напряжения по фазе на угол : 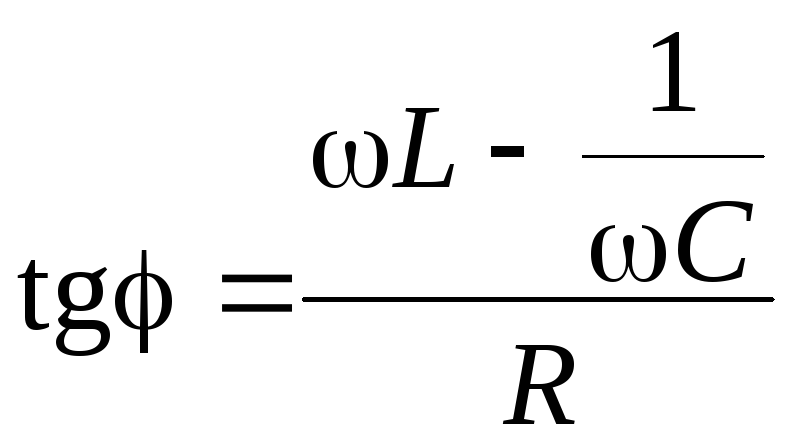. Если<0, ток опережает напряжение.

Полное электрическое сопротивление (импеданс) равно

,

где R – активное сопротивление,– реактивное индуктивное сопротивление,– реактивное емкостное сопротивление.

Ток на индуктивности отстаёт от напряжения на π/2, а ток на емкости опережает напряжение наπ/2. Выражениепредставляет собой реактивное сопротивление или реактанс.

С учётом сказанного Таким образом, если значения сопротивленийRиXотложить вдоль катетов треугольника, то длина гипотенузы будет численно равнаZ (рис.10).

Рис. 10

Мощность, выделяемая в цепи переменного тока , равна

Из тригонометрии . ТогдаСреднее значениеобозначимр. Среднее значение, тогда

.

Однако тогда(рис.11).

Рис. 11

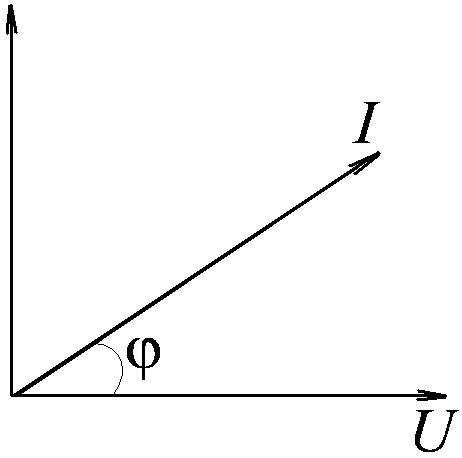
Такую же мощность развивает постоянный ток силойЭто значение силы тока называется эффективным или действующим.

Аналогично действующее значение напряжения.

Тогда средняя мощность; величинаназывается коэффициентом мощности. Чем меньше,тем ближек 1, тем больше мощность.