2 Методы измерения сдвиговой вязкости

2.1 Введение

Область знания, охватывающую проблемы экспериментального изучения вязкости различных сред, называют вискозиметрией, а приборы предназначенные для измерения вязкости – вискозиметрами.

Круг таких приборов, отличающихся принципом действия конструкцией, очень широк. Можно выделить обширный класс ротационных вискозиметров, в которых контролируемые узлы работают в режиме вращения; класс капиллярных вискозиметров, в которых контролируется режим течения через капилляр. Достаточно разнообразны конструкции, в которых тела различной формы обтекаются средой, а также устройства для косвенного определения вязкости по какому-либо параметру от вязкости зависящему, например, ультразвуковые вискозиметры. Выбор того или иного метода и конструкции вискозиметра определяется характером среды, диапазоном значений вязкости и т. д.

В настоящем пособии рассмотрены только методы, нашедшие применение в предлагаемых далее экспериментальных заданиях.

2.2 Капиллярный метод

Рассмотрим течение (достаточно медленное) жидкости (газа) в трубе (капилляре, канале). Течение будет слоистым, а конвективный перенос массы в поперечном потоку направлении будет отсутствовать. В этом направлении будет происходить лишь перенос импульса. Скорость течения на стенках трубы равна нулю (вследствие прилипания), в середине же трубы она имеет наибольшее значение. В точках цилиндрических поверхностей, равноудаленных от оси трубы, скорость течения постоянна. Отдельные концентрические слои скользят один по другому и при том так, что скорость везде имеет осевое направление. Это ламинарное течение (от латинского Lamina – cлой). Если рассматривать гидродинамически установившееся течение на участке трубы (достаточно удаленном от концов трубы), то распределение скоростей вдоль радиуса не зависит от продольной координаты (рис. 3) и изменяется по параболическому закону:

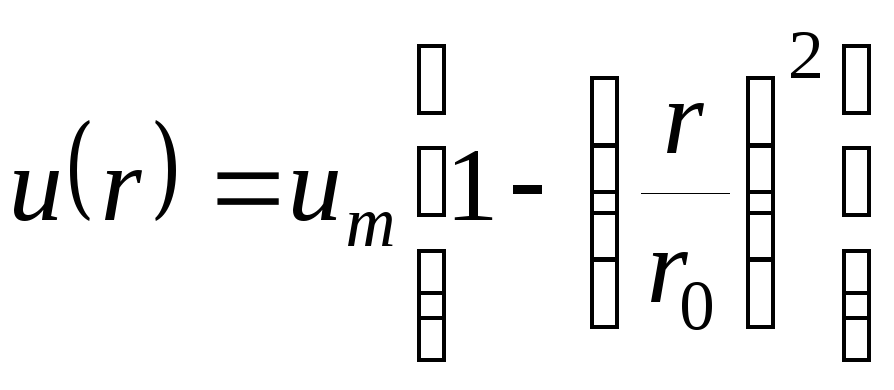, (11)

Рис. 3 Радиальное распределение скоростей слоев при течении жидкости в трубе

где и_т – скорость на оси, r₀ – радиус трубы, r – текущий радиус.

Движение каждого элемента среды будет ускоряться вследствие перепада давления и замедляться из-за напряжения сдвига, вызванного трением.

Вырежем мысленно цилиндр длиной l и радиусом у, соосный трубе. В направлении оси х на цилиндр действуют силы давления и, приложенные к левому и правому торцам. Кроме того, на боковую поверхность цилиндра действует касательная сила (тормозящая), обусловленная вязкостью среды

.

Приравнивая разность сил давления касательной силе, получим условие равновесия сил в направлении координаты х при равномерном течении:

, откуда

. (12)

После разделения переменных и интегрирования получим выражение для скорости как функция координаты у:

. (13)

Константу интегрирования с найдем из граничного условия:

при .

Тогда из (13) следует: . В итоге получим:

. (14)

Сравнивая (14) и (11), находим максимальную скорость на оси трубы:

. (15)

Объемный расход среды Q (м³/с), протекающей со скоростью и через некоторое сечение , равен

.

В данном случае объемный расход будет равен объему параболоида вращения, т. е. половине произведения площади основания параболоида на его высоту:

. (16)

В механике жидкости и газа полученное выражение известно как закон Хагена-Пуазейля. Эту зависимость обычно используют для экспериментального определения динамической вязкости.

2.3 Метод Стокса (метод падающего шарика)

Рассмотрим суть метода применительно к исследованию жидкости. Хотя он может быть использован и при исследовании любых других вязких сред.

Рис. 4 Силы, действующие на падающий шарик

Если в жидкость опустить тело со сферической поверхностью, плотность которого больше плотности жидкости, то оно начнет двигаться вниз сначала ускорено, а затем равномерно. Равномерность его движения будет обусловлена равенством нулю суммы действующих на него сил (рис. 4).

–выталкивающая сила;

–сила, обусловленная вязкостью жидкости;

–сила тяжести.

В режиме равномерного движения

или в скалярной форме в проекции на ось у

. (17)

На рисунке 5 показано распределение скоростей, соседних слоев жидкости, увлекаемых шариком. В непосредственной близости к его поверхности скорость слоя жидкости равна скорости шара, а по мере удаления уменьшается и, практически, становится равной нулю на некотором расстоянии.

Рис. 5 Распределение скоростей слоев среды, вызванное движущимся шариком

Стокс рассмотрел движение шарика радиусом r в вязкой жидкости и нашел, что сила вязкого сопротивления движению F_η пропорциональна скорости и шарика, вязкости η жидкости и выражается формулой:

, (18)

которая носит название закона Стокса.

Выталкивающую силу Архимеда можно представить в виде

, (19)

где ρ_ж – плотность жидкости.

Сила тяжести равна

, (20)

где ρ_Т – плотность шарика.

В соответствии с уравнением (17) имеем

,

откуда следует соотношение для η

. (21)

Это соотношение справедливо, если шарик падает в безграничной среде. Если падение шарика происходит в цилиндрическом сосуде, то в формулу (21) необходимо добавить поправочный коэффициент, учитывающий влияние стенок цилиндра на движение шарика

, (22)

где R – радиус цилиндра.

Поправка теоретически обоснована Ладенбургом.

2.4 Метод «падающего кольца»

При использовании этого метода осуществляется движение тонкого металлического кольца в слое жидкости между двумя неподвижными стенками, образованными наружным Н и внутренним В цилиндрами. На рисунке 6 показан разрез основного экспериментального узла в диаметральной плоскости.

Рис. 6 Разрез рабочего узла установки

При вертикальном расположении оси ОО установки кольцо под действием силы тяжести движется вниз сначала ускоренно, а затем равномерно. Режим равномерного движения устанавливается при равенстве нулю суммы, действующих на кольцо сил. На рис. 6 эти силы указаны приложенными в центре масс кольца:

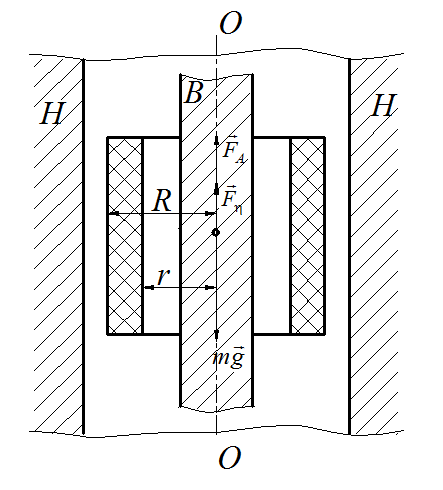
или в скалярной форме

. (23)

где – выталкивающая (Архимедова) сила; – сила вязкого трения; – сила тяжести кольца.

Поскольку , где ρ_ж – плотность жидкости, v_к – объем кольца, то ее значение можно представить в виде:

, (24)

где l – высота кольца, R и r – соответственно радиусы наружной и внутренней поверхности кольца.

Для вязкой силы можно записать

, (25)

где η – коэффициент вязкости, S – полная площадь «трущейся» поверхности кольца; Δz – градиент скорости, равный, в данном случае d, поскольку в зазоре шириной d скорость жидкости изменяется от и – (скорость кольца) – до нуля (у неподвижных стенок).

Поверхность S равна

. (26)

Подставляя (2), (3), (4) в выражение (1) получим:

,

где ρ_к – плотность материала кольца.

Отсюда для динамической вязкости имеем:

или

. (27)

Величина составляет константу данной экспериментальной установки. .

Таким образом, для определения динамической вязкости надо измерить скорость и движения кольца.

Приведенные рассуждения справедливы при неограниченной протяженности зазора с жидкостью. Конечная длина его оказывает влияние на режим движения кольца. Поэтому более точно константу А определяют с помощью эталонной жидкости с известной вязкостью, проводя калибровочные измерения.