
Математическая индукция 1к ПИвЭ
.doc
ТИПОВОЕ ЗАДАНИЕ №1
Дисциплина:
Математический анализ
1 курс ПИЭ
Тема:
«Математическая индукция и бином Ньютона»
1. Математическая индукция.
-
Вычислить сумму

-
Вычислить сумму

-
Доказать, что
 .
. -
Доказать,что
 .
. -
Доказать, что

-
Доказать, что

-
Доказать, что

-
Доказать, что

-
Вычислить

-
Доказать тождество

-
Упростить выражение
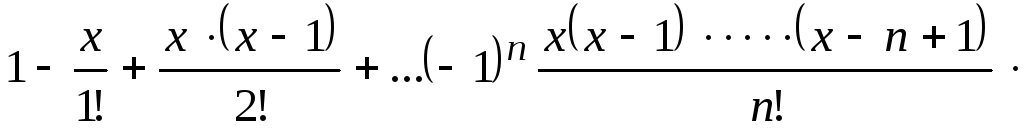
-
Доказать, что сумма кубов трёх последовательных натуральных чисел делится на 9.
-
Доказать, что при любом целом
 выражение
выражение
 делится на 133.
делится на 133. -
Доказать, что

-
Доказать, что
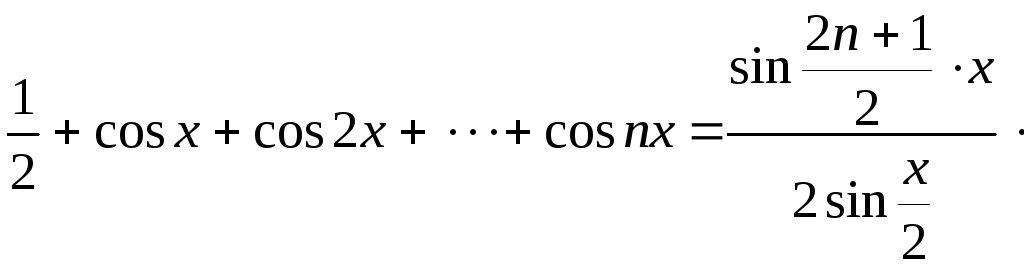
-
Доказать, что

-
Доказать, что
 делится на 19.
делится на 19. -
Доказать, что
 .
. -
Доказать, что
 .
. -
Доказать, что
 .
. -
Доказать, что для всех n>1
 .
. -
Доказать, что для всех n>1
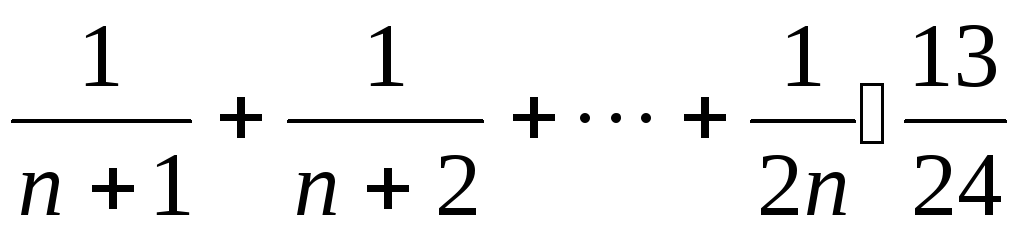 .
. -
Доказать, что для всех n>1
 .
. -
При каких натуральных n верно неравенство:
 ?
? -
При каких натуральных n верно неравенство:
 ?
? -
При каких натуральных n верно неравенство: n4<4n?
-
Доказать, что n5-n делится на 5 для любого натурального числа n.
-
Доказать, что n7-n делится на 7 при любом натуральном n.
-
Вычислить (1+32+52+…+(2n-1)2+…+1992)- (22+42+62…+(2n)2+…+2002).
-
Доказать, что при любом натуральном n выполняется равенство
 .
.
2. Бином Ньютона.
-
В разложении
 коэффициент
третьего члена на 44 больше коэффициента
второго члена. Найти свободный от x
член разложения.
коэффициент
третьего члена на 44 больше коэффициента
второго члена. Найти свободный от x
член разложения. -
Сколько рациональных членов содержится в разложении:

-
Найти номер того члена разложения
 ,
который содержит a и
b в одинаковых степенях.
,
который содержит a и
b в одинаковых степенях.
-
Найти тот член разложения
 ,
который не зависит от x,
если сумма биноминальных коэффициентов
равна 128.
,
который не зависит от x,
если сумма биноминальных коэффициентов
равна 128. -
Отношение коэффициента пятого члена к коэффициенту третьего члена разложения
 равно
2,5. Найти третий член разложения.
равно
2,5. Найти третий член разложения. -
Найти средний член разложения
 ,
если коэффициент третьего члена равен
28.
,
если коэффициент третьего члена равен
28. -
Доказать, что выражение
 делится на 9 при любом натуральном
делится на 9 при любом натуральном
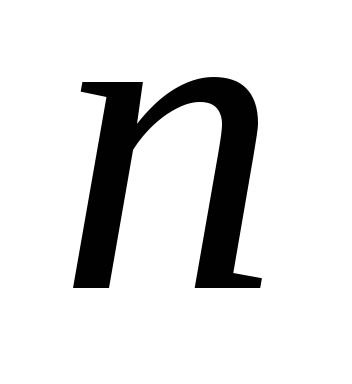
-
Каков наибольший коэффициент разложения
 ,
если сумма всех коэффициентов равна
4096?
,
если сумма всех коэффициентов равна
4096? -
Сумма коэффициентов второго и третьего членов разложения
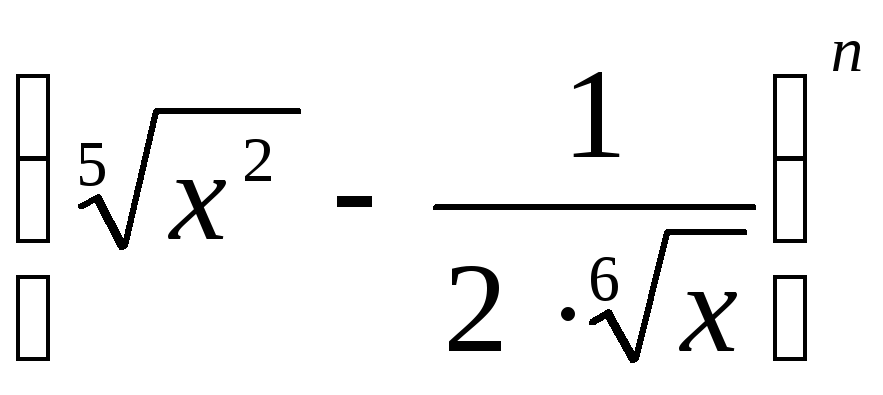 равна 25,5. Найти член, не содержащий
равна 25,5. Найти член, не содержащий
 .
. -
Сумма третьего от начала и третьего от конца биноминальных коэффициентов разложения
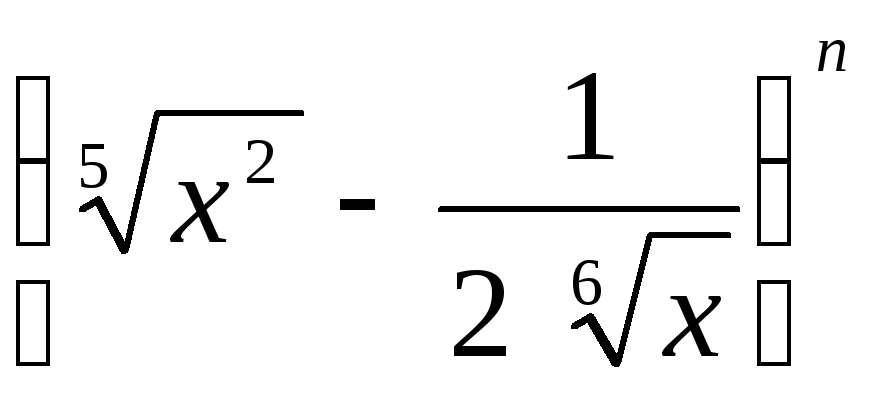 равна 9900. Сколько рациональных членов
содержится в этом разложении?
равна 9900. Сколько рациональных членов
содержится в этом разложении? -
Третье слагаемое разложения
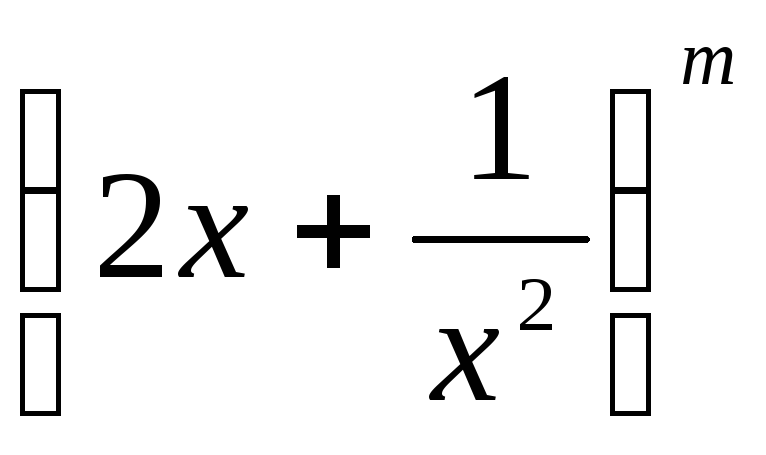 не
содержит x . При каких
значениях x это слагаемое равно
второму слагаемому разложения
не
содержит x . При каких
значениях x это слагаемое равно
второму слагаемому разложения
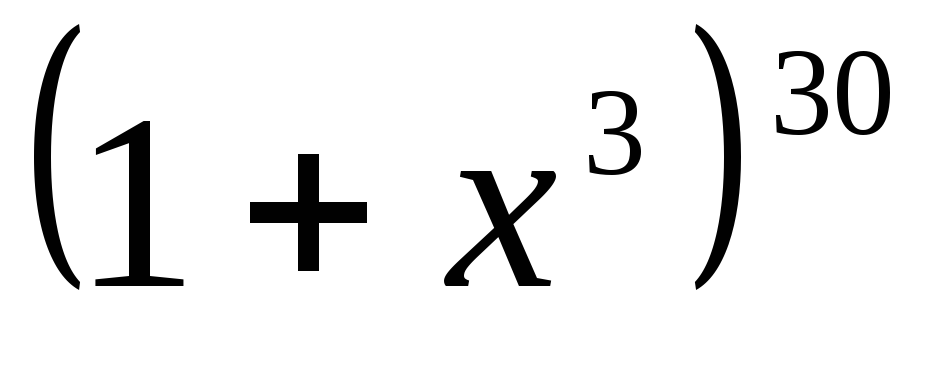 ?
? -
При любом допустимом значении
 слагаемое
слагаемое
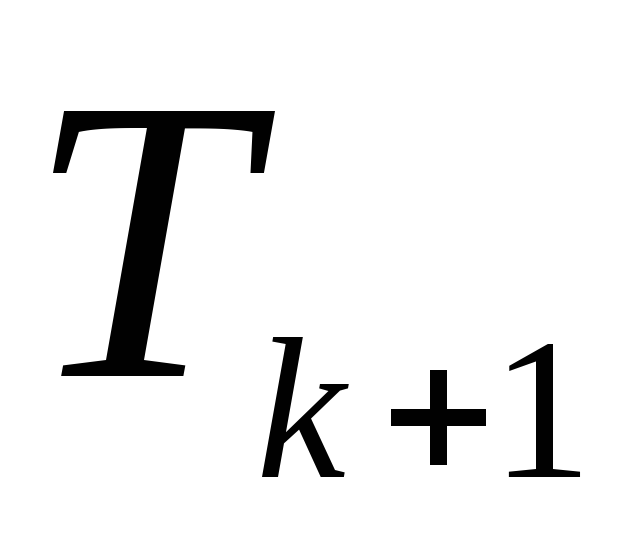 разложения
разложения
 в
2 раза меньше слагаемого
в
2 раза меньше слагаемого
 разложения
разложения
 .
Найти эти слагаемые.
.
Найти эти слагаемые.
-
Найти k-тый член разложения
 ,
если известно, что
,
если известно, что
 .
.
-
Разность между некоторыми членами
 и
и
 разложения
разложения
 равна
30. Определить, при каких x
это возможно, если член
равна
30. Определить, при каких x
это возможно, если член
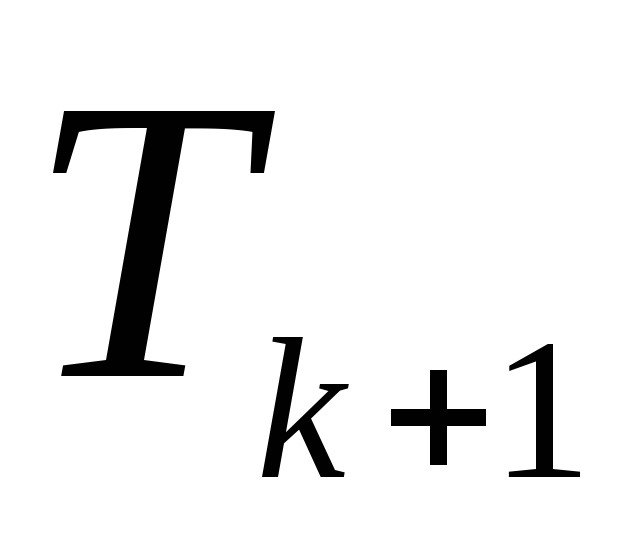 содержит x в степени,
вдвое меньшей, чем член
содержит x в степени,
вдвое меньшей, чем член
 .
.
-
Найти наибольший биноминальный коэффициент разложения
 ,
если произведение четвёртого слагаемого
от начала и четвёртого слагаемого от
конца равно 14400.
,
если произведение четвёртого слагаемого
от начала и четвёртого слагаемого от
конца равно 14400.
-
Сумма нечётных биноминальных коэффициентов разложения
 равна 512. Найти слагаемое, не содержащее
x.
равна 512. Найти слагаемое, не содержащее
x.
-
Найти член разложения
 ,
не зависящий от x.
,
не зависящий от x.
-
Найти средний член разложения
 ,
не производя разложения.
,
не производя разложения.
-
Найти наибольший коэффициент многочлена
 .
.
-
Найти коэффициент разложения (1+3x+2x3)10 при x4.
-
Найти сумму коэффициентов разложения (13x3-7x-5)100.
-
Вычислить
 .
.
-
Найти седьмой член разложения (
 )13.
)13.
-
Найти член разложения
 ,
не зависящей от a.
,
не зависящей от a.
-
Найти член разложения
 ,
содержащий x8.
,
содержащий x8.
-
Найти член разложения
 ,
содержащий x1980.
,
содержащий x1980.
-
Найти члены разложения
 ,
являющиеся целыми числами.
,
являющиеся целыми числами.
-
Сколько членов разложения
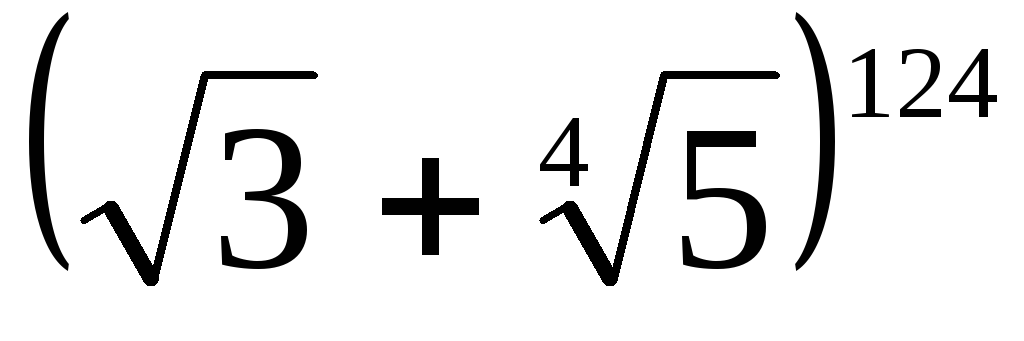 являются целыми числами?
являются целыми числами?
-
Найти наибольший коэффициент многочлена
 .
.
-
Найти сумму коэффициентов многочлена
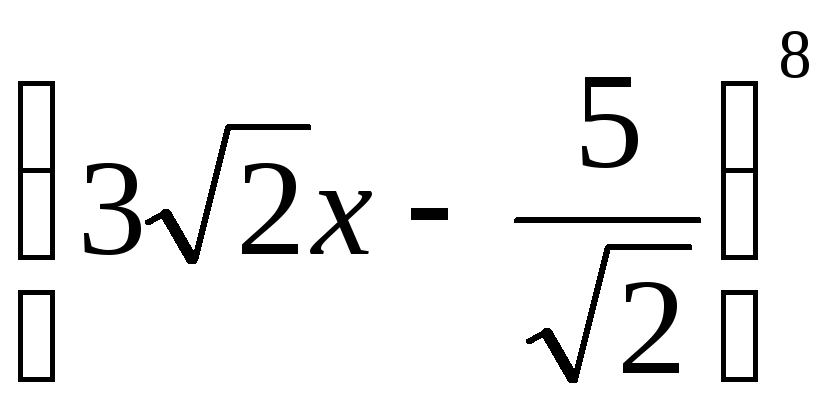 .
.
Задача
1.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
2.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
3.
а). Доказать, что
![]() ;
;
б). Найти
![]()
4.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
5.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
6.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
7.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
8.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
9.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
10.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
11.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
12.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
13.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
14.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
15.
а). Доказать, что
![]() ;
;
б). Найти
![]() ;
;
а). Доказать, что
![]() ;
;
б). Найти
![]() .
.
