
Конспект часть 1 (1)
.pdf
Пирсон показал, что если взять ci = n , то при больших n закон распределе- pi
ния величины U практически не зависит от функции распределения F(x) и от чис- ла опытов n, а будет определяться только числом разрядов k. При увеличении n
закон распределения выбранной таким образом функции
U = χ 2 |
k |
(p* − p |
)2 |
|
|
= nå |
i |
i |
|
|
|
|
pi |
|
|
||
|
i =1 |
|
(6.2) |
||
приближается к «распределению хи-квадрат». Сама функция в этом случае обо-
значается как U = χ 2 . Для удобства вычислений функцию расхождения
хи-квадрат приводят к виду
U = χ 2 |
k |
(m |
i |
− np |
)2 |
|
|
= å |
|
i |
|
. |
(6.3) |
||
|
|
npi |
|
||||
|
i =1 |
|
|
|
|
|
Здесь mi – количество попаданий случайной величины в i-ый интервал.
Распределение χ2 зависит от параметра ν, называемого «числом степеней свободы» распределения. Число степеней свободы ν равно числу разрядов минус число независимых условий (связей), наложенных на частоты p*i. Примерами та-
ких связей могут быть:
k
1) å pi* = 1 , {это должно быть всегда};
i =1
k
2) åxi pi* = mx , {среднее арифметическое должно совпадать с математическим
i =1
ожиданием};
3) åk (xi − x )2 pi* = Dx . {Должны совпадать теоретическая и выборочная диспер-
i =1
сии}.
Могут быть другие связи.
Для распределения χ2 составлены специальные таблицы. Пользуясь ими,
можно для каждого значения χ2 и числа степеней свободы ν найти вероятность p
того, что величина, распределенная по закону χ2, превзойдет это значение.
Распределение χ2 дает возможность оценить степень согласованности теоре-
тического и статистического распределений. Будем исходить из того, что величи- на X действительно распределена по закону F(x). Тогда вероятность p, опреде-
ленная по таблице, есть вероятность того, что за счет чисто случайных причин
мера расхождения теоретического и статистического распределений будет не
43
меньше, чем полученное значение χ2. Если эта вероятность p мала, то результат
опыта следует считать противоречащим гипотезе о том, что закон распределения
случайной величины Х есть F(x).
Таким образом, соответствие теоретического и статистического распределе- ний проводится в следующей последовательности:
1). Определяется мера расхождения
χ 2 |
k |
(m − np )2 |
||
= å |
i |
i |
. |
|
|
|
|||
|
i =1 |
|
npi |
|
2). Определяется число степеней свободы
ν=k – s , где s – число наложенных связей.
3). По ν и χ2 по таблице определяется вероятность того, что величина, имею-
щая распределение χ2 с ν степенями свободы, будет иметь отклонение, большее,
чем наблюдаемое в опыте χ2 .
Насколько мала должна быть вероятность р для того, чтобы отвергнуть гипо-
тезу о совпадении распределений, является неопределенным вопросом. На прак-
тике, если p < 0,1 , необходимо проверить эксперимент и в случае повторения ре-
зультатов попытаться подобрать другой закон распределения.
Следует отметить, что с помощью критерия χ2 можно только лишь опроверг- нуть гипотезу, что распределения совпадают. Если вероятность р велика, то этот факт только свидетельствует, что наблюдаемое статистическое распределение
не противоречит теоретическому распределению.
Если вероятность р, определенная по таблице, очень велика, то здесь следу- ет обратить внимание на другую сторону проблемы. Если получили табличную вероятность р=0,99 , то это будет означать, что с вероятностью 0,99 расхождения должны быть больше, чем наблюдаемые в опытах. Тогда можно признать, что расхождение является не случайным, а вызвано другими причинами, например подчисткой данных, когда не все результаты вносятся в протокол измерений. По такой схеме проверяются результаты выборов, опросов и т.д.
Для примера рассмотрим обработку результатов стрельб. Было произведено 500 выстрелов. Результаты отклонения попаданий от центра мишени сведены в
статистический ряд.
i |
-4,-3 |
-3,-2 |
-2,-1 |
-1,0 |
0,1 |
1,2 |
2,3 |
3,4 |
|
|
|
|
|
|
|
|
|
mi |
6 |
25 |
72 |
133 |
120 |
88 |
46 |
10 |
P*i |
0,012 |
0,05 |
0,144 |
0,266 |
0,24 |
0,176 |
0,092 |
0,02 |
44
Вычислим среднее арифметическое и выборочную дисперсию, считая, что ве-
личина внутри интервала принимает значение, равное середине интервала
mx* |
= -0,012 ´ 3,5 - 0,05 ´ 2,5 - 0,144 ´1,5 - 0,266 ´ 0,5 + 0,24 ´ 0,5 + |
|
|
+ 0,176 ´1,5 + 0,092 ´ 2,5 |
+ 0,02 ´ 3,5 = 0,168 |
Dx* |
= å8 (xi - mi* )2 pi* = (- 3,5 - |
0,168)2 ´ 0,012 + (- 2,5 - 0,168)2 ´ 0,05 + |
i=1
+(-1,5 - 0,168)2 ´ 0,144 + (- 0,5 - 0,168)2 ´ 0,266 + (0,5 - 0,168)2 ´ 0,24 +
+(1,5 - 0,168)2 ´ 0,176 + (2,5 - 0,168)2 ´ 0,092 + (3,5 - 0,168)2 ´ 0,02 = 2,098 .
Предположим, что разброс значений имеет нормальное распределение. Тогда
принимаем, что m = mx* |
= 0,168 ; |
σ 2 = Dx* = 2,098; σ = 1,448 . |
|||||||||||||||
Плотность распределения отклонений |
|||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
- |
(x -0,168)2 |
|
||
|
|
f (x) = |
|
|
|
|
|
|
|
|
e |
2×2,098 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1,448 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2p |
|
|
|
|
|
|||||||||
Найдем вероятности попадания в разряды по формуле |
|||||||||||||||||
|
|
æ xi +1 - m ö |
|
æ xi - m |
ö |
||||||||||||
|
|
pi = Фç |
|
|
|
|
|
÷ - |
Фç |
|
|
÷ |
|||||
|
|
|
|
|
σ |
|
σ |
||||||||||
|
|
è |
|
|
|
ø |
|
è |
ø |
||||||||
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
p1 |
æ |
- 3 - 0,168 ö |
= Ф(- 2,1878) = 0,0144 ; |
||||||||||||||
= Фç |
1,448 |
|
|
|
÷ |
||||||||||||
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
æ |
- 2 - 0,168 ö |
- 0,0144 = Ф(-1,4972)- 0,0144 = 0,0672 - 0,0144 = 0,0528 |
||||||||||||||
= Фç |
1,448 |
|
|
|
÷ |
||||||||||||
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
p3 |
æ |
-1- 0,168 ö |
- 0,0672 = Ф(- 0,8066)- 0,0672 = 0,2100 - 0,0672 = 0,1428 |
||||||||||||||
= Фç |
1,448 |
|
|
|
÷ |
||||||||||||
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
p4 |
æ |
0 - 0,168 ö |
- 0,2100 |
= Ф(- 0,1160)- 0,2100 = 0,4538 - 0,2100 = 0,2438 |
|||||||||||||
= Фç |
1,448 |
|
÷ |
||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||
p5 |
æ |
1- 0,168 ö |
|
|
|
|
|
|
|
= Ф(0,5746)- 0,4538 = 0,7142 - 0,4538 = 0,2604 |
|||||||
= Фç |
1,448 |
|
÷ - 0,4538 |
||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||
p6 |
æ |
2 - 0,168 ö |
- 0,7142 |
= Ф(1,2652)- 0,7142 = 0,8971- 0,7142 = 0,1829 |
|||||||||||||
= Фç |
1,448 |
|
÷ |
||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||
p7 |
æ |
3 - 0,168 ö |
- 0,8971 |
= Ф(1,9558)- 0,8971= 0,9747 - 0,8971= 0,0776 |
|||||||||||||
= Фç |
1,448 |
|
÷ |
||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
||
p8 = 1- 0,9747 = 0,0253
45

Умножив эти вероятности на количество выстрелов n=500, получим теорети- ческие частоты попадания в каждый из интервалов. Сопоставим теоретические и
статистические частоты
i |
|
-4,-3 |
|
-3,-2 |
|
-2,-1 |
|
|
|
-1,0 |
|
0,1 |
|
1,2 |
|
|
|
2,3 |
3,4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
mi |
|
|
|
6 |
|
25 |
|
|
72 |
|
|
|
|
133 |
|
120 |
|
88 |
|
|
|
|
46 |
10 |
|||||
pin |
|
|
|
7,2 |
|
26,4 |
|
71,4 |
|
121.9 |
|
130,2 |
|
91,45 |
|
|
38,8 |
12,65 |
|||||||||||
Рассчитаем величину критерия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
χ 2 |
8 |
(m − np )2 |
|
|
(6 − 7,2)2 |
|
(25 − 26,4)2 |
|
(72 − 71,4)2 |
|
(133 −121,9)2 |
||||||||||||||||||
= å |
i |
i |
= |
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
+ |
||||||
npi |
|
|
7,2 |
|
|
|
26,5 |
|
|
|
71,4 |
|
|
|
121,9 |
|
|||||||||||||
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
+ |
(120 −130,2)2 |
|
+ |
(88 − 91,45)2 |
|
+ |
(46 − 38,8)2 |
+ (10 −12,65)2 |
= 4,11 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
38,8 |
|
|
|
|
||||||||||||||||||
|
|
|
|
130,2 |
|
|
|
|
|
91,45 |
|
|
|
|
|
|
|
12,65 |
|
|
|
|
|
||||||
Число степеней свободы ν = 8 – 3 = 5. По таблице находим:
для χ2=3,00 р=0,7;
для χ2=4,35 р=0,5;
Интерполяцией находим
p = 0,7 + (0,5 − 0,7) 4,11− 3,00 = 0,536 . 4,35 − 3,00
Эта вероятность малой не является, поэтому гипотезу о том, что разброс ре- зультатов подчиняется нормальному закону, можно считать правдоподобной.
46
Лекция 10. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Как правило, результаты опыта описываются не одной, а несколькими случай-
ными величинами, образующими комплекс или систему. Свойства системы не- скольких случайных величин не исчерпываются свойствами отдельных составля-
ющих величин, но также включают связи между случайными величинами. Систему двух случайных величин X,Y можно изобразить в виде случайной точки на плоско-
сти XY. Аналогично система трех случайных величин представляется точкой в трехмерном пространстве, n случайных величин - точкой в n-мерном простран-
стве. Иногда систему случайных величин рассматривают в виде n-мерного слу- чайного вектора, каждая из проекций которого на координатные оси является слу- чайной величиной.
Так же, как и для одномерного случая, наиболее полное описание поведения системы случайных величин производится с помощью законов распределения: интегрального закона - функции распределения и дифференциального закона - плотности распределения. В некоторых случаях бывает достаточным описать по- ведение системы с помощью некоторых числовых характеристик, описывающих средние значения составляющих систему случайных величин, их разброс относи- тельно средних значений, а также тесноту связи между входящими в систему слу- чайными величинами.
Наиболее просто и наглядно представляется система двух случайных вели-
чин. Функцией распределения системы двух случайных величин (X,Y) называется вероятность совместного выполнения двух неравенств X<x, Y<y:
F(x,y ) = P((X < x),(Y < y )) . (7.1)
Функция распределения F(x,y) есть вероятность попадания случайной точки (X,Y) в бесконечный квадрант с вершиной в точке (x,y), лежащий левее и ниже ее.
Основные свойства функции распределения: |
|
|||
1. |
Функция распределения F(x,y) есть неубывающая функция обоих своих ар- |
|||
гументов, то есть |
|
|
|
|
|
при x2>x1 |
F(x2,y)³ F(x1,y) |
; |
|
|
при y2>y1 |
F(x,y2)³ F(x,y1) |
. |
|
2. |
Повсюду на -¥ функция распределения равна нулю: |
|
||
|
F(x, -¥)=F(-¥,y)=F(-¥,-¥)=0 |
. |
(7.2) |
|
47
3. При одном из аргументов, равном +∞, функция распределения системы
превращается в функцию распределения случайной величины, соответствующей
другому аргументу:
F(x, +∞)=F1(x), |
F(+∞,y)=F2(y). |
(7.3) |
4. Если оба аргумента равны +∞, то функция распределения системы равна 1:
F(+∞,+∞)=1 . |
(7.4) |
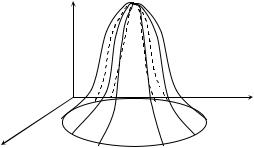
С помощью функции распределения можно найти вероятность попадания слу- чайной точки в заданную область R. Если она представляет собой прямоугольник с вершинами α,β,γ,δ, то, согласно рис.7.1, эта вероятность выразится формулой:
P((X,Y ) R) = F(β,δ)− F(β,γ)− F(α,δ)+ F(α,γ).
|
|
|
|
|
(7.5) |
|
|
|
y |
|
|
Функция распределения существует |
|
|
|
|
|
|
|
|
|
δ |
|
|
|
для любых случайных величин, прерыв- |
|
|
|
|
||||
|
|
|
|
|
ных и непрерывных. Однако, для непре- |
|
|
|
|
|
|
рывных случайных величин закон распре- |
|
|
γ |
|
|
|
||
|
|
|
||||
|
|
|
|
|
деления характеризуют обычно плотно- |
|
|
|
|
|
|
||
|
|
|
|
х |
стью распределения. |
|
|
|
α |
β |
|
Для одной случайной величины плот- |
|
Рис.7.1. К определении вероятности |
||||||
ность распределения представляет собой |
||||||
попадания случайной величины в |
||||||
прямоугольную область |
|
|
предел отношения вероятности попадания |
|||
на малый участок к длине этого участка. Аналогично определяется плотность рас- пределения системы двух случайных величин представляется как предел отно-
шения вероятности попадания на малую площадь к величине этой площади.
Пусть имеется система двух случайных величин (X,Y), которая интерпретиру-
ется случайной точкой на плоскости xOy. Рассмотрим на этой плоскости малый
прямоугольник R со сторонами |
x и y, примыкающий к точке с координатами (x,y) |
|
Вероятность попадания случайной величины в этот прямоугольник |
|
|
P((x,y ) R) = F(x + x, y + |
y )− F(x + x, y )− F(x,y + y )+ F(x, y ) . |
(7.6) |
Разделим вероятность попадания в прямоугольник на площадь прямоугольни-
ка и возьмем предел этого отношения при стремлении площади к нулю
48
|
|
|
lim x→0 |
P((X,Y ) R) |
= |
|
|
|
|
|
|
|
|||
x y |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
y →0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
F(x + x,y + y) − F(x + x,y) − F(x,y + y) + F(x,y) |
= |
∂ 2F(x,y) |
||||||||
|
|
|
= lim x→0 |
|
|
|
|
x |
y |
|
|
∂x∂y |
|||
|
|
|
|
y →0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.7) |
Эту величину определим как плотность распределения функции |
|
|
|||||||||||||
|
|
|
|
|
f (x,y ) = |
∂ 2F(x,y ) |
. |
|
|
|
|
|
(7.8) |
||
|
|
|
|
|
|
|
∂x∂y |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрически |
|
плотность |
|
|
|
|
|
|
|
|
|
|
|
|
|
распределения |
можно |
предста- |
|
|
|
|
f(X,Y) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
вить как поверхность, аналогич- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ную кривой распределения. Если |
|||
|
|
|
|
|
|
|
|
|
|
|
|
пересечь поверхность распреде- |
|||
|
|
|
|
|
|
|
|
|
X |
|
|
ления плоскостью, параллельной |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Y |
|
|
|
|
|
|
|
оси xOy, то получим замкнутую |
||||||
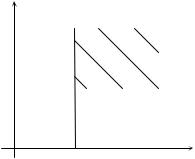
Рис.7.2. Поверхность плоскости распределения |
|
кривую, плотность на которой по- |
|||||||||||||
|
стоянна. На |
топографических |
|||||||||||||
системы двух случайных величин X и Y |
|
|
|
картах аналогично изображаются |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
поверхности равного уровня. |
|||
Вероятность попадания случайной величины в произвольную область D |
|||||||||||||||
|
|
|
|
P((X,Y ) D) = òòf (x,y)dxdy |
. |
|
|
|
(7.9) |
||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
Вероятность попадания случайной величины в прямоугольник с вершинами |
|||||||||||||||
(α,γ), (β,γ), (α,δ), (β,d) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
βδ |
|
|
|
|
|
|
|
|
||
|
|
|
P((X,Y ) D) = ò òf (x,y )dx dy |
|
. |
|
|
(7.10) |
|||||||
αγ
Функция распределения в точке (х,у)
x |
y |
|
F(x,y ) = ò |
òf (x,y )dx dy . |
(7.11) |
−∞ −∞
Основные свойства плотности распределения: |
|
1. Плотность распределения системы есть функция неотрицательная |
|
f (x,y ) ³ 0 . |
(7.11) |
2.Двойной интеграл в бесконечных пределах от функции распределения ра-
вен единице
49
+∞ +∞ |
|
ò òf (x,y )dxdy = 1. |
(7.12) |
−∞ −∞
Геометрически эти свойства соответствуют тому, что, во-первых, вся область
плотности распределения находится не ниже плоскости xOy и, во-вторых, объем под поверхностью плотности распределения равен единице.
Зная закон распределения системы, можно найти законы распределения от-
дельных величин
F1(x) = F(x,∞) = |
x |
+∞ |
|
||||||
ò |
òf (x,y )dxdy , |
(7.13) |
|||||||
|
|
|
|
|
|
−∞ −∞ |
|
||
откуда, дифференцируя по x, получим |
|
||||||||
|
dF1(x) |
|
+∞ |
|
|
||||
f1(x) = |
= |
òf (x,y )dy . |
(7.14) |
||||||
|
dx |
||||||||
|
|
|
−∞ |
|
|
||||
|
|
|
|
|
|
|
|||
Аналогично |
|
|
|
|
|
|
|
|
|
F2(y) = F(∞,y) = |
+∞ y |
|
|||||||
ò |
òf (x,y)dxdy , |
(7.15) |
|||||||
|
|
|
|
|
|
−∞ −∞ |
|
||
f2(y) = |
|
dF2 |
(y) |
= |
+∞ |
|
|
||
|
òf (x,y )dx . |
(7.16) |
|||||||
|
dy |
|
|||||||
|
|
|
|
−∞ |
|
|
|||
|
|
|
|
|
|
|
|
||
Обратная задача в общем случае невозможна. Нельзя, зная законы распре-
деления отдельных величин, найти закон распределения системы величин. Для этого дополнительно должна быть информация о зависимости между этими вели- чинами. Эта зависимость может быть охарактеризована с помощью условных за- конов распределения. Условным законом распределения величины Х, входящей в систему (Х,Y), называется ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y.
Условный закон распределения можно задавать как функцией, так и плотно-
стью распределения. Условная функция распределения случайной величины Х
обозначается Fy(x), условная плотность распределения fy(x). Зная закон распре-
деления одной величины и условный закон распределения другой, можно соста- вить закон распределения системы.
50
Y |
dx |
1 |
|
|
dy |
y |
|
2 |
|
|
|
0 |
x |
Х |
|
||
|
|
|
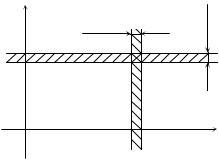
Рис.7.3. К определению условных |
||
законов распределения |
||
Рассмотрим элементарный прямоуголь-
ник Rd со сторонами dx, dy. Вероятность по- падания в этот прямоугольник равна вероят-
ности одновременного попадания случайной точки (X,Y) в элементарную полосу 1, опира-
ющуюся на отрезок dx, и в полосу 2, опираю- щуюся на отрезок dy:
f (x,y )dx dy = P((X,Y )Ì Rd ) = P((x < X < x + dx)(y < Y < y + dy )).
Эта вероятность равна вероятности попадания случайной точки в элементар-
ную полосу 1, умноженную на условную вероятность попадания в элементарную
полосу 2, вычисленную при условии, что первое событие, т.е. Х=х, имело место.
Тогда
f (x,y )dx dy = f1(x)dx × fx (y )dy . |
|
Отсюда |
|
f (x,y ) = f1(x)×fx (y ) |
(7.17) |
или |
|
f (x,y ) = f2 (y )×fy (x) . |
(7.18) |
51
Лекция 11. ТЕСНОТА СВЯЗИ МЕЖДУ ДВУМЯ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ
Случайные величины могут быть зависимыми друг от друга или независимы-
ми. Случайная величина Y называется независимой от случайной величины X,
если закон распределения величины Y не зависит от того, какое значение приняла величина Х. В этом случае
f (x,y ) = f1(x)×f2 (y ) .
Существуют два типа зависимостей: функциональная и вероятностная или стохастическая. Две величины называются функционально зависимыми, если,
зная значение одной величины, можно точно указать значение другой. Вероят-
ностная зависимость имеет более общий характер. Если величина Y связана с величиной X вероятностной зависимостью, то, зная значение X, можно лишь ука- зать закон распределения Y, зависящий от того, какое значение приняла величина
X, но не значение Y.
Вероятностная зависимость может быть более или менее тесной. По мере увеличения тесноты вероятностная зависимость переходит в функциональную.
Как правило, величины, считающиеся функционально зависимыми, в действи-
тельности связаны весьма тесной вероятностной зависимостью, при заданном значении одной из них другая колеблется в столь узких пределах, что ее значение
можно считать вполне определенным. С другой стороны, многие величины, счи-
тающиеся независимыми, в действительности находятся в некоторой взаимной зависимости, но эта зависимость настолько слаба, что для практических целей ею можно пренебречь. Если случайные величины X и Y находятся в вероятностной зависимости, то это означает, что с изменением величины X величина Y имеет тенденцию также изменяться. Эта тенденция выполняется в среднем, но в каждом отдельном случае от нее возможны отступления.
Систему случайных величин X,Y характеризует положение на плоскости xOy. Характеристиками положения являются математические ожидания mx и my. Гео-
метрически это координаты точки на плоскости, вокруг которой происходит рассе- яние. Дисперсии Dx и Dy характеризуют рассеяние случайной величины в направ- лении осей Оx и Оy. Тесноту связи характеризует корреляционный момент Kxy.
Для непрерывных величин
Kxy = +∞ò +∞ò(x - mx )(y - my )f (x,y)dxdy ,
−∞ −∞
(7.19)
52
