
- •3.4. Нечёткая и лингвистическая переменные
- •3.5. Основы нечеткой логики
- •3.6. Нечёткие выводы, используемые в экспертных и управляющих системах
- •1. Алгоритм Mamdani
- •1. Центроидный метод (Centroid Defuzzification Method)
- •2. Первый максимум (First of Maxima)
- •3. Средний максимум (Middle of Maxima)
- •5. Высотная дефазификация (Height Defuzzification)
1. Алгоритм Mamdani
Данный алгоритм соответствует рассмотренному примеру 3.32 и рис. 3.15. Математически он может быть описан следующей последовательностью действий:
Приведение к нечёткости –- для предпосылок каждого правила находятся степени истинности высказываний, составляющих конъюнктивную композицию: х1(х0),у1(у0),х2(х0),у2(у0).
Выполнение нечёткого вывода – для предпосылок каждого из правил находятся уровни «отсечения» функций принадлежности, соответствующих лингвистическим значениям переменной вывода, с использованием операции «минимум». Обозначим истинность предпосылки первого правила а1, второго правила –а2:
a1=min(х1(х0),у1(у0)),
a2=min(х2(х0),у2(у0)). (3.71)
Затем находятся «усечённые» функции принадлежности, соответствующие лингвистическим значениям переменной вывода:
’z1(z) = min(a1, z1(z)),
’z2(z) = min(a2, z2(z)). (3.72)
Композиция – с использованием операции «максимум» производится объединение найденных нечётких множеств, описываемых усечёнными функциями принадлежности ’z1(z),’z2(z), что приводит к получению итогового нечёткого множества для переменной выходаСzс функцией принадлежности(z):
Сz=C’z1C’z2, (3.73)
(z) =max(’z1(z),’z2(z)). (3.74)
Приведение к чёткости – для нахождения искомого чёткого значения выходной переменной z0может быть использован любой метод приведения к чёткости, например, цетроидный метод.
Заключительным этапом нечёткого логического вывода является дефазификация, илиприведение к чёткости. В некоторых из рассмотренных алгоритмов этот этап объединён с этапом собственно логического вывода, в других – выделен как самостоятельный, причем метод приведения к чёткости может быть выбран лицом, принимающим решение.
Обозначим искомое чёткое значение выходной переменной z0и рассмотрим наиболее часто используемые методы приведения к чёткости.
1. Центроидный метод (Centroid Defuzzification Method)
Центроидный метод определения чёткого значения выходной переменной уже упоминался при рассмотрении общей схемы нечёткого логического вывода: чёткое значение выходной переменной z0определяется как координата центра тяжести для кривой(z).
Для непрерывного варианта:
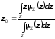 . (3.80)
. (3.80)
Для дискретного варианта используется уже упоминаемое выражение (3.77):
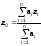 .
.
2. Первый максимум (First of Maxima)
При использовании этого метода дефазификации чёткая величина переменной вывода находиться как наименьшее значение, при котором достигается максимум итогового нечёткого множества:
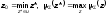 . (3.81)
. (3.81)
Иллюстрацией этого метода приведения к чёткости служит рис. 3.19.
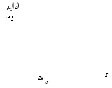
Рис.3.19. Определение чёткого значения переменной вывода с использованием критерия первого максимума
3. Средний максимум (Middle of Maxima)
Чёткое значение выходной переменной определяется по формуле:
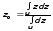 , (3.82)
, (3.82)
где, u– подмножество элементовz, максимизирующих итоговое нечёткое подмножество.
Для дискретного варианта используется следующее выражение:
 , (3.83)
, (3.83)
где N– количество элементовz, доставляющих максимум итогового нечёткого подмножества.
Приведение к чёткости с использованием критерия среднего максимума проиллюстрировано на рис. 3.20.
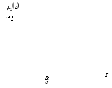
Рис. 3.20. Определение чёткого значения переменной вывода с использованием критерия среднего максимума
4. Критерий максимума (Max–Criterion)
При использовании этого метода чёткое значение переменной вывода выбирается произвольно среди множества элементов z*u, доставляющих максимум итогового нечёткого подмножества:
z0 {z*(z*)=
{z*(z*)=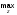 (z)
}. (3.84)
(z)
}. (3.84)
