Рабочая тетр2
.doc3. Рациональные и иррациональные уравнения
и неравенства
5
2.
Постройте графики функций, составив
таблицу контрольных точек,
а)
;
|
х
|
|
|
|
|
|
у
|
|
|
|
|
б
)
;
|
х
|
|
|
|
|
|
у
|
|
|
|
|
в)
|
х
|
|
|
|
|
|
у
|
|
|
|
|
53. Решите уравнения
а)
;
Указания: Решайте уравнения согласно алгоритму:
|
1) Перенесите все слагаемые в левую часть |
|
|
2) Приведите слагаемые к общему знаменателю |
|
|
3) Запишите систему, которая определяет условие равенства дроби нулю |
|
|
4) Решите уравнение, определяющее равенство нулю числителя |
|
|
5) Сделайте проверку
|
|
|
6) запишите ответ |
|
б)
;
в)
.
Указания: Чтобы
упростить решение, можно ввести замену
переменной:
,
а далее решать согласно алгоритму.
54. Решите неравенства методом интервалов
а)
Указания: Найдите в справочнике алгоритм решения неравенств методом интервалов и решайте согласно алгоритму.
б)
.
в)
.
г)
.
д)
55.
Решить систему неравенств
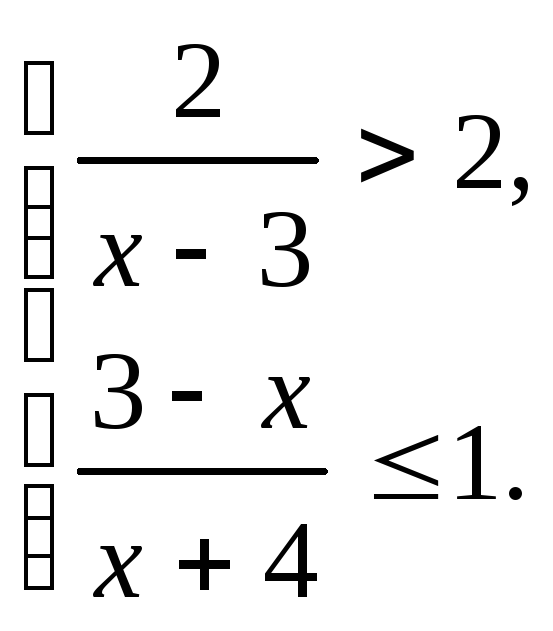
Указание: Решить каждое неравенство методом интервалов; пересечь полученные решения.
56.
Решить совокупность неравенств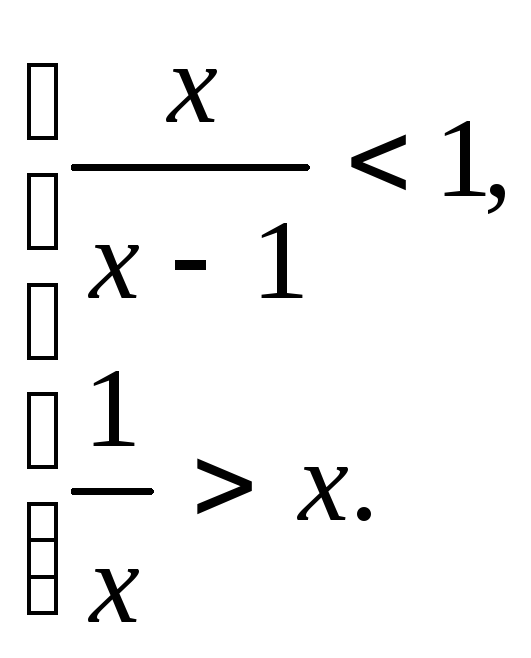
Указание: Решить каждое неравенство методом интервалов; объединить полученные решения.
57. Решите уравнения
а)
;
Указания: Найдите в справочнике тему «Иррациональные уравнения». Решайте уравнения методом возведения обеих частей уравнения в степень корня. Не забудьте сделать проверку!
б)
;
в)
58. Решите уравнения
а)
Указания: Произведение множителей равно нулю, когда один из множителей равен нулю, а другой имеет смысл. Т.е.
или
.
б)
в)
59. Решите неравенства
а)
.
б)
.
в)
.
г)
.
4. Показательная функция.
Показательные уравнения и неравенства
60. П
остройте
графики функций, составив таблицу
контрольных точек,
а)
;
|
х
|
|
|
|
|
|
|
|
у
|
|
|
|
|
|
|
б
)
;
|
х
|
|
|
|
|
|
|
|
у
|
|
|
|
|
|
|
в)
|
х
|
|
|
|
|
|
|
|
у
|
|
|
|
|
|
|
61. Найдите показательные уравнения и подчеркните их.
|
1)
|
4)
|
|
2)
|
5)
|
|
3)
|
6.
|
;
;
;
;
;
.62. Решите уравнения
а)
;
Указание. Найдите в справочнике тему «Показательные уравнения» и примените метод уравнивания оснований.
б)
;
в)
.
63. Решите уравнения
а)
.
Указание. Посмотрите решение примера 5.7 в [1] на с. 49.
б)
.
64. Решите уравнения
а)
.
Указание. Введите замену переменной.
б) Решите уравнение
65. Найдите в [1] на с. 45 свойства показательной функции.
а) В следующих двух утверждениях вставьте пропущенное слово: «возрастает» или «убывает».
1) При
>1
показательная функция
__________ на всей числовой оси.
2) При 0<
<1
показательная функция
__________ на всей числовой оси.
б) В следующих двух утверждениях вставьте пропущенное слово «больше » или «меньше».
1) При
>1
большему значению аргумента показательной
функции
соответствует __________ значение этой
функции, и наоборот, при
>1
большему значению показательной функции
соответствует __________ значение аргумента
этой функции.
2) При 0<
<1
большему значению аргумента показательной
функции
соответствует __________ значение этой
функции, и наоборот, при 0<
<1
большему значению показательной функции
соответствует __________ значение аргумента
этой функции.
в) В следующих утверждениях после знака
равносильности (
)
напишите нужное неравенство:
или
.
1) При
>1:
_________
2) При 0<
<1:
_________
3) При
>1:
_________
4) При 0<
<1:
_________
г) В следующих утверждениях после знака
равносильности (
)
напишите нужное неравенство:
или
.
1) При
>1:
_________
2) При 0<
<1:
_________
3) При
>1:
_________
4) При 0<
<1:
_________
Этими утверждениями вы будете пользоваться при решении показательных неравенств.
66. Решите неравенства
а)
.
Указание. Запишите число 8 как степень числа 2. Ответ запишите сначала неравенством, а потом в виде интервала.
б)
.
в)
.
г)
.
-
Найдите области определения функций
а)
.
б)
.
-
Решите неравенства
а)
Указание. Посмотрите решение примера 5.14 в [1] на с. 52.
б) Решите неравенство
5. Логарифмическая функция.
Логарифмические уравнения и неравенства
69. Напишите определение логарифма
положительного числа b
по основанию
,
где
и
(см. [1], c. 53).
Из определения логарифма получаем,
что при
и
справедливо утверждение
.
Используйте это утверждение при решении следующих четырёх уравнений.
70. Решите уравнения
а)
.
б)
.
в)
.
г)
.
Запишите основное логарифмическое тождество (см. [1], c. 53.).
71. Решите уравнение
.
Указание. Используйте основное логарифмическое тождество.
72. Прочитайте основные свойства логарифмов (см. [1], c. 54 и с. 55.) и запишите формулу для логарифма произведения двух положительных чисел.
73. Найдите
,
если
,
.
74. Решите уравнения
а)
.
б)
.
75. Запишите формулу для логарифма частного двух положительных чисел.
76. Найдите
,
если
,
.
77. Решите уравнение
.
-
Запишите формулу для логарифма степени.
-
Вычислите
а)
,
если
,
.
б)
,
если
,
.
в)
,
если
.
г)
,
если
.
80. Решите уравнение
Указание: используйте метод потенцирования (смотрите решение примера 6.14 в [1] на с.62). Не забудьте про ОДЗ или сделайте проверку найденных решений!
80. В следующих двух утверждениях вставьте пропущенные знаки: «=», или «<», или «>».
Указание: используйте свойства логарифмической функции ([1], стр.57.)
1) При
логарифмическая функция
возрастает на промежутке
.
Поскольку
__ 0, то
__ 0 при
и
__ 0 при
.
2) При
логарифмическая функция
убывает на промежутке
.
Поскольку
__ 0, то
__ 0 при
и
__ 0 при
81. Используя эти утверждения, определите знак следующих чисел (после каждого из них напишите «>0» или «<0»):
___
___
___
___
___
___
82. В следующих утверждениях после
знака равносильности (
)
напишите нужное неравенство:
или
.
1) При
>1:
_________
2) При 0<
<1:
_________
3) При
>1:
_________
4) При 0<
<1:
_________
83. В следующих утверждениях после
знака равносильности (
)
напишите нужное неравенство:
или
.
1) При
>1:
_________
2) При 0<
<1:
_________
3) При
>1:
_________
4) При 0<
<1:
_________
Этими утверждениями вы будете пользоваться при решении логарифмических неравенств.
84. Решите неравенства
а)
.
Указание. Представьте обе части неравенства в виде логарифмов по одному основанию.
б)
.
в)
.
г)
.
д)
.
Указание. Определите знак числа в знаменателе.
е)
.
85. Найдите область определения
функции
.